уметь:

1. применять определения для решения задач логики;

2. применять загоны логики для упрощения логических выражений;

3. строить таблицы истинности и логические функции;

Рекомендации:

1. разобрать примеры;

2. выполнить задания по данной теме

3. выполнить индивидуальное задание

Примеры:

1. Примеры высказываний:

1. Москва – столица России.

2. Число 27 является простым.

3. Волга впадает в Каспийское море.

Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.

Следующие предложения высказываниями не являются:

• Давай пойдем гулять.

• 2*x>8.

• a*x2+b*x+c=0.

• Который час?

Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.

Примеры записи сложных высказываний с помощью обозначения логических связок:

1. "Быть иль не быть - вот в чем вопрос." (В. Шекспир) А V ¬ A <=> В

2. "Если хочешь быть красивым, поступи в гусары." (К. Прутков) А => В

2. Построение логической функции по ее таблице истинности:

Попробуем решить обратную задачу. Пусть дана таблица истинности для некоторой логической функции Z(X,Y):

Составить логическую функцию для заданной таблицы истинности.

3. Упрощение формул.

Законы логики и правила преобразования логических выражений

1. Закон двойного отрицания (двойное отрицание исключает отрицание):

А = .

2. Переместительный (коммутативный) закон:

   1. для логического сложения: А  B = B  A;

   2. для логического умножения: A & B = B & A.

Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.

3. Сочетательный (ассоциативный) закон:

   1. для логического сложения: (А  B)  C = A  (B  C);

   2. для логического умножения: (A & B) & C = A & (B & C).

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

4. Распределительный (дистрибутивный) закон:

   1. для логического сложения: (А  B) & C = (A & C)  (B & C);

   2. для логического умножения: (A & B)  C = (A  C) & (B  C).

Закон определяет правило выноса общего высказывания за скобку.

5. Закон общей инверсии (законы де Моргана):

   1. для логического сложения: = &;

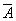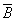   2. для логического умножения: =   

6. Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):

   1. для логического сложения: А  A = A;

   2. для логического умножения: A & A = A .

Закон означает отсутствие показателей степени.

7. Законы исключения констант:

   1. для логического сложения: А  1 = 1, А  0 = A;

   2. для логического умножения: A & 1 = A, A & 0 = 0.

8. Закон противоречия:

   1. A & = 0.

Невозможно, чтобы противоречащие высказывания были одновременно истинными.

9. Закон исключения третьего:

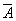   1. A  = 1.

Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.