УДК 519. 63 (076.1)

ББК 22.193 я 73

Г 686

Г 686 Гореликов, А.В. Практикум на ЭВМ для студентов старших курсов специальности «прикладная математика и информатика»: Учеб. пособие / А.В. Гореликов, А.В. Ряховский; Сургут. гос. ун-т. – Сургут: Изд-во СурГУ, 2010. – 32с.

Пособие соответствует дисциплине ОПД.Ф.07 «Практикум на ЭВМ» государственного образовательного стандарта высшего профессионального образования по специальности: 010501.65(2) - «прикладная математика и информатика».

Рассмотрены основные этапы получения численного решения на конкретном примере начально-краевой задачи. Приведен пример программы численного решения задач для уравнения теплопроводности. Содержит 70 краевых и начально-краевых задач для самостоятельного решения.

Предназначено для студентов 4 – 5 курсов специальности «прикладная математика и информатика» факультета информационных технологий СурГУ.

Табл. 1. Илл. 1. Библиогр.: 7 назв.

Печатается по решению редакционно-издательского совета Сургутского государственного университета.

Рецензент:

Моргун Д.А., канд. физ.-мат. наук, доц. кафедры прикладной математики Сургутского государственного университета.

© Гореликов А.В., Ряховский А.В.

© Сургутский государственный

университет, 2010

Пример численного решения начально-краевой задачи Постановка задачи и математическая модель

Необходимо получить численное решение смешанной начально-краевой задачи (1)-(4) для одномерного уравнения теплопроводности, в котором коэффициент теплопроводности линейно зависит от температуры. Результаты расчетов нужно сравнить с аналитическим решением (5).

, :

; (1)

; (2)

; (3)

. (4)

Аналитическое решение:

. (5)

Построение расчетной сетки

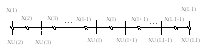
Рис. 1 Расчетная сетка

Расчетная область разбивается на непересекающиеся контрольные объемы и в центре каждого контрольного объема находится расчетная точка (Рис.1). Координаты граней контрольных объемов содержатся в массивеXU(I), ( I = 2, …, L1 ), а координаты самих расчетных точек в массиве X(I), ( I = 1, …, L1 ). Расчетные точки на границах области (X(1), X(L1)) не имеют собственных контрольных объемов и располагаются на гранях контрольных объемов прилегающих к границе области.

Дискретный аналог

Для получения дискретного аналога уравнения теплопроводности используется метод контрольного объема [1-2] и полностью неявная схема при интегрировании по времени. Если уравнение нелинейно, то при решении для учета нелинейности используются внутренние итерации. Предполагается, что источниковый член в уравнении теплопроводности линеаризован, т.е. представлен в виде (), (подробности в [1-2]). Уравнение теплопроводности интегрируется по контрольному объему для произвольной точкиX(I) и по интервалу времени от t₀ до t₁ (t₁ - t₀ = Δt):

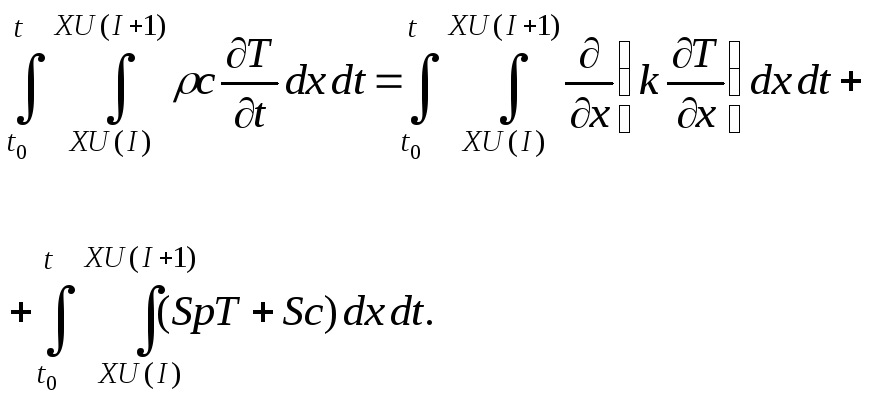(6)

Плотность и теплоемкостьзадаются в точкахX(I), сеточные значения содержатся в массивеRHO(I). Коэффициент теплопроводности задается на гранях контрольных объемов ( в точкахXU(I)), сеточные значения содержатся в массивеGAMI(I). В результате интегрирования получается уравнение:

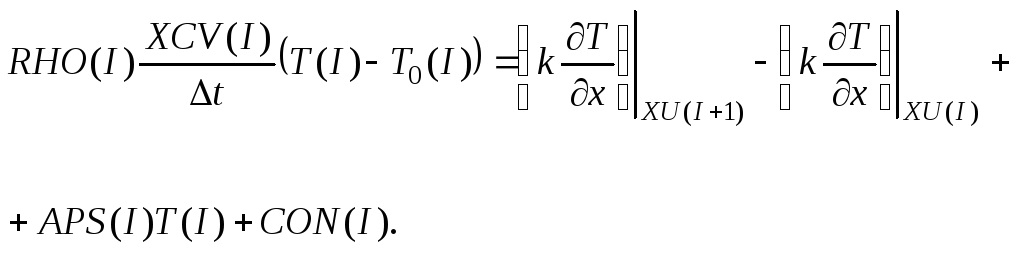(7)

Где, индекс 0 означает, что величина берется с предыдущего временного слоя t₀,; ‑ размер контрольного объема. Сеточные значенияинаходятся в массивах,CON(I), APS(I), соответственно.

Тепловые потоки на гранях контрольного объема аппроксимируются следующим образом:

;

(8)

.

В результате, дискретный аналог для одномерного уравнения теплопроводности может быть записан в виде:

, (9)

где

; ;

; ; (10)

.

В задаче (1)-(4) уравнение однородно, и следовательно, для данной задачи:

CON(I) = 0; APS(I) = 0, ( I = 3, …, L1-2 ); (11)

также очевидно, что:

RHO(I) = 1, ( I = 2, …, L1-1 ). (12)

Уравнение (1) нелинейно , коэффициент теплопроводности на внутренних гранях контрольных объемов рассчитывается по формуле:

, (13)

т.е. как среднее арифметическое. Для учета нелинейности используются внутренние итерации.

Граничные условия

На левой границе задано граничное условие второго рода:

, и , следовательно, тепловой поток через левую границу равен:

. (14)

Но T(1) неизвестно. С другой стороны, этот поток аппроксимируется по формуле (8) для I = 2:

, (15)

Приравнивая правые части формул (14) и (15) и учитывая, что можно получить следующее соотношение междуT(1) и T(2):

. (16)

Подстановка (16) в (14) дает следующее выражение для теплового потока через левую грань контрольного объема (I = 2):

. (17)

Таким образом, в дискретном аналоге, для контрольного объема, примыкающего к левой границе, отсутствует T(1) и следовательно и тогда необходимо положить. Из формулы (17) следует, что в дискретном аналоге дляI = 2 появляется дополнительный источниковый член, для которого:

, . (18)

На правой границе задано граничное условие третьего рода (3):

, которое можно записать в виде:

. (19)

С другой стороны, из (8) для I = L2 :

. (20)

Сумма (19) и (20) дает:

, (21)

что позволяет, учитывая , записать тепловой поток через правую границу в виде:

. (22)

Таким образом, в дискретном аналоге, для контрольного объема, примыкающего к правой границе, можно положить и считать, что тепло проходящее через правую границу выделяется внутри контрольного объема. Тогда из (22) следует, что в дискретном аналоге дляI = L2 появляется дополнительный источниковый член, для которого:

, (23)

. (24)

Формула для определения T(L1) получается из (19) и (20) и имеет вид:

. (25)