
- •Министерство образования российской федерации
- •Содержание
- •Предисловие
- •Лабораторная работа № 1 измерение коэффициента теплопроводности воздуха методом нагретой нити
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 2 измерение удельной теплоёмкости воздуха при постоянном давлении
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 3 определение изменения энтропии при фазовом переходе
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 4 Измерение отношения изобарной и изохорной теплоёмкостей газа
- •Введение
- •Описание экспериментальная установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 5 Определение коэффициента внутреннего трения в жидкости
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 6 Определение коэффициента внутреннего трения и средней длины свободного пробега молекул воздуха
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 7
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения упражнения
- •Обработка результатов измерений
- •Описание экспериментальной установки
- •Порядок выполнения упражнения
- •Обработка результатов измерений
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 9 Изучение распределения Максвелла
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 10 Определение коэффициента теплопроводности металла
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 11 Изготовление и градуировка датчика температуры на основе термопары
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения упражнения
- •Описание экспериментальной установки
- •Порядок выполнения упражнения и обработка результатов измерений
- •Описание экспериментальной установки
- •Порядок выполнения упражнения и обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 12 Измерение электрической проводимости водных растворов электролитов
- •Введение
- •Описание экспериментальной установки
- •Порядок выполнения упражнения
- •Обработка результатов измерений
- •Порядок выполнения упражнения
- •Обработка результатов измерений
- •Контрольные вопросы
- •Литература
- •Лабораторный практикум по молекулярной физике и термодинамике Методические указания к лабораторным работам по курсу общей физики
- •626400, Россия, Ханты-Мансийский автономный округ,
Обработка результатов измерений
1.
Рассчитать среднее значение диаметра
каждого шарика
![]() ,
средние диаметры свинцовых и пластмассовых
шариков возвести в квадрат, а для
пластмассовых шариков еще и в куб. Данные
занести в таблицы соответственно
материалам шариков.
,
средние диаметры свинцовых и пластмассовых
шариков возвести в квадрат, а для
пластмассовых шариков еще и в куб. Данные
занести в таблицы соответственно
материалам шариков.
2.
Просчитать плотность каждого пластмассового
шарика по формуле ρ = 6m/(π![]() 3),
данные занести в таблицу 2. Рассчитать
3),
данные занести в таблицу 2. Рассчитать
![]() – среднюю плотность пластмассовых
шариков, ее значение занести в данные
установки.
– среднюю плотность пластмассовых
шариков, ее значение занести в данные
установки.
3.
Убедиться в том, что движение шариков
ламинарное, т.е. выполняется
пропорциональность FС
(при турбулентном, вихревом движении
FС
2).
Измерить для каждого шарика скорость
падения
= L/t.
Затем построить графики зависимости
от
![]() 2
(для двух сред). Если экспериментальные
точки на этих зависимостях укладываются
на прямую линию, то это будет означать,
что формулы (4) и (6) справедливы для
данного опыта
2
(для двух сред). Если экспериментальные
точки на этих зависимостях укладываются
на прямую линию, то это будет означать,
что формулы (4) и (6) справедливы для
данного опыта
4.
По формуле (6) определить значение
для каждого шарика и занести результат
измерения в таблицу. Определить среднее
значение
![]() исследуемых жидкостей и погрешность
его измерения.
исследуемых жидкостей и погрешность
его измерения.
5.
Сравнить экспериментальные значения
![]() с табличными, сделать вывод.
с табличными, сделать вывод.
Контрольные вопросы
1. Что называется вязкостью? Каков механизм вязкости жидкости?
2. Напишите уравнение движения шарика в цилиндре, заполненном вязкой жидкостью.
3. Какое движение называется ламинарным, турбулентным?
4. Как зависит вязкость жидкости от температуры и относительной молекулярной массы?
5. Каков физический смысл имеет коэффициент внутреннего трения (вязкости) ?
6. Какие силы действуют на шарик, падающий в жидкости?
7. Как вычисляется сила вязкого трения по закону Ньютона, как она направлена, отчего зависит?
8. Почему измерения коэффициента вязкости по методу Стокса верны только при малых скоростях движения шарика?
9. Как в данной работе определяется коэффициент вязкости?
10. Указать на схеме (рис.3) направление градиента скорости и потока импульса для явления переноса, моделируемого данным опытом.
Лабораторная работа № 6 Определение коэффициента внутреннего трения и средней длины свободного пробега молекул воздуха
Цель работы: экспериментальное определение коэффициента внутреннего трения воздуха; определение средней длины свободного пробега молекул воздуха.
Введение
Рассмотрим поток газа, известно, что скорость течения слоев газа в потоке различна. Такое состояние газа не является равновесным, и в нем будут происходить процессы, стремящиеся выровнять скорость течения. Эти процессы называются внутренним трением (вязкостью). Подобно тому, как при теплопроводности возникает поток тепла из более нагретых в менее нагретые участки среды, так и при внутреннем трении, благодаря тепловому движению молекул, происходит передача импульса от более быстрых участков потока к менее быстрым.
Можно ввести понятие о потоке импульса J: это есть полный импульс, переносимый в 1 сек в положительном направлении Х через площадку S, перпендикулярную оси Х. Можно также утверждать, что поток импульса пропорционален градиенту скорости течения u:
![]() , (1)
, (1)
где
![]() - проекция градиента скорости на ось X
,
- коэффициент динамической вязкости
газа.
- проекция градиента скорости на ось X
,
- коэффициент динамической вязкости
газа.
х
Рис.1


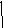
![]()
![]()



 S
S
Пусть
в направлении, перпендикулярном оси х,
течет газ. Скорость течения изменяется
от слоя к слою. Мысленно выделим два
слоя газа, скорости которых
![]() и
и![]() соответственно, и разделяющую их площадку
S (рис. 1). В некоторый момент эти слои
обладают импульсами
соответственно, и разделяющую их площадку
S (рис. 1). В некоторый момент эти слои
обладают импульсами![]() и
и![]() ,
направления которых совпадают с
направлениями скоростей
,
направления которых совпадают с
направлениями скоростей![]() и
и![]() .
Так как все молекулы участвуют еще и в
тепловом движении, то они непрерывно
переходят из одного слоя в другой. В том
и другом направлениях в единицу времени
через площадкуS
переходит одинаковое число молекул. В
результате теплового движения между
соседними слоями газа, через какое-то
время, происходит выравнивание их
импульсов и скоростей. Это и обуславливает
вязкость газов.
.
Так как все молекулы участвуют еще и в
тепловом движении, то они непрерывно
переходят из одного слоя в другой. В том
и другом направлениях в единицу времени
через площадкуS
переходит одинаковое число молекул. В
результате теплового движения между
соседними слоями газа, через какое-то
время, происходит выравнивание их
импульсов и скоростей. Это и обуславливает
вязкость газов.
Найдем
поток импульса через площадку S,
перпендикулярную оси х. Для всех молекул
при данной температуре газа примем
среднюю скорость теплового движения
равной ср.
Предположим также, что тепловые скорости
молекул, равномерно распределены по
трем взаимно перпендикулярным
направлениям. Тогда из всех молекул n,
заключенных в единице объема, 1/3 движется
по оси х, и из них половина движется в
положительном направлении оси х, т.е.
по направлению к площадке, в то время
как другая половина движется в
противоположном направлении - от
площадки. Расстояние между слоями газа
можно подобрать таким образом, чтобы
молекулы пролетали до площадки без
столкновений, т.е. это расстояние должно
быть равно длине свободного пробега
молекул - .
Пусть
![]() >
>![]() .
.
Поток импульса через площадку S слева направо равен произведению импульса молекулы mu1, на число молекул, пересекающих площадку S за единицу времени:
![]() (2)
(2)
Запишем аналогичное выражение для потока импульса справа налево:
![]() (3)
(3)
Результирующий поток определяется выражением:
![]()
Так как u1 = u + u, а u2 = u - u , где u - скорость молекул слоя площадки S, получим:
![]() (4)
(4)
Умножим
и разделим (4) на λ, и учтем, что при
ламинарном течении справедливо
выражение:![]() .
Окончательно получим:
.
Окончательно получим:
![]() (5)
(5)
Так как mn = (плотность газа):
![]() . (6)
. (6)
Коэффициент пропорциональности называют динамической вязкостью или коэффициентом динамической вязкости:
![]() (7)
(7)
Это выражение для вязкости впервые было получено Ньютоном. Единицей динамической вязкости является паскаль-секунда:
![]()
Поскольку
~ p, а
~![]() ,
то динамическая вязкость газа не зависит
от давления, но зависит от рода газа и
его температуры. Наряду с динамической
вязкостью используется кинематическая
вязкость:
,
то динамическая вязкость газа не зависит
от давления, но зависит от рода газа и
его температуры. Наряду с динамической
вязкостью используется кинематическая
вязкость:![]()
O
r+dr
L
O/
Рис.а
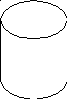

 r
r
Наличие
сил внутреннего трения приводит к
возникновению градиента скорости
![]() .
Очевидно, что наибольшая скорость
течения воздуха будет на оси симметрии
капилляраOO/.
Вырежем мысленно в газе цилиндрический
слой с внутренним радиусом
r, внешним
радиусом r + dr. На этот слой со стороны
более быстрых слоев действует “ускоряющая”
сила внутреннего трения:
.
Очевидно, что наибольшая скорость
течения воздуха будет на оси симметрии
капилляраOO/.
Вырежем мысленно в газе цилиндрический
слой с внутренним радиусом
r, внешним
радиусом r + dr. На этот слой со стороны
более быстрых слоев действует “ускоряющая”
сила внутреннего трения:
![]() ,(8)
,(8)
где S - площадь боковой поверхности цилиндра (S=2rL).
Течение воздуха через капилляр радиусом r0 происходит под действием перепада давлений на концах капилляра р1 - р2.
Интегрируя уравнение (8) по всей площади поперечного сечения (от r = 0 до r = r0) получим:
![]() , (9)
, (9)
где V - объем воздуха, протекающего через капилляр, - время истечения данного объема воздуха.
