Архив1 / docx31 / Лабораторная работа 1

Задание

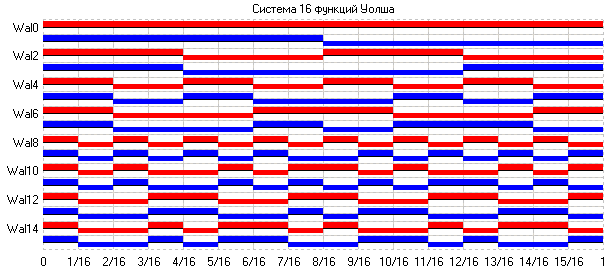
1) Механизм формирования спектра Уолша.

Задание: изучить расчет коэффициентов Ск спектра Уолша на примере прямоугольных и синусоидальных колебаний. Внести в отчет расчет ненулевых коэффициентов Ск.

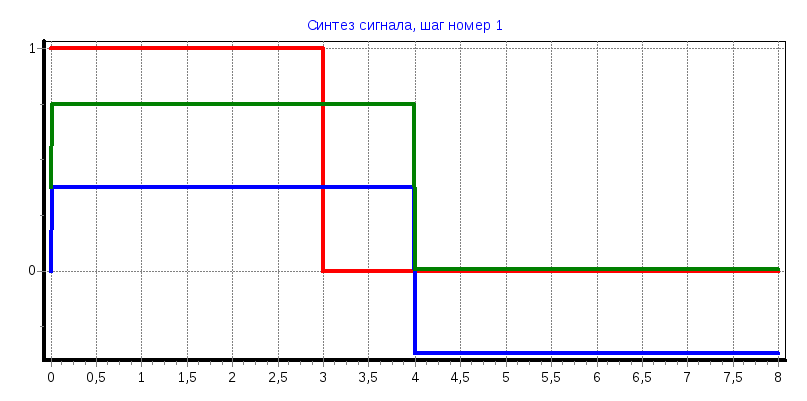
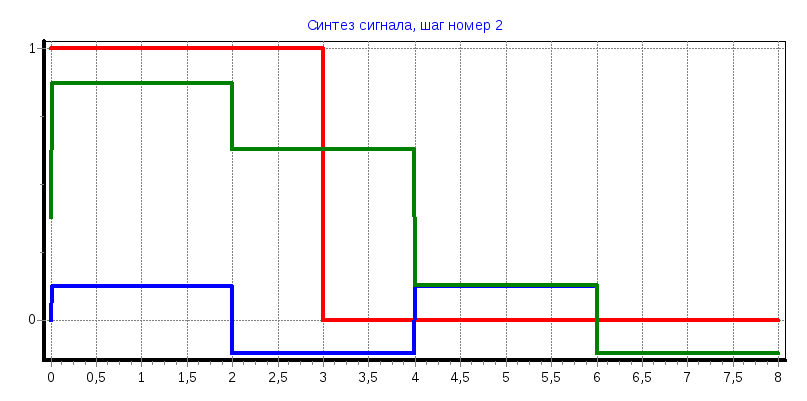
2) Синтез с использованием 16 функций Уолша.

Задание: получить восстановленные с помощью функций Уолша сигналы:

• Прямоугольные импульсы (изменять длительность tu = 2, 3, 4 мс);

• Пилообразные импульсы (ничего не изменять);

• Синусоидальные колебания (изменять начальную фазу = 0, 45, 90);

Зарисовать сигналы и их спектры (кроме случаев, когда Ск = 0).

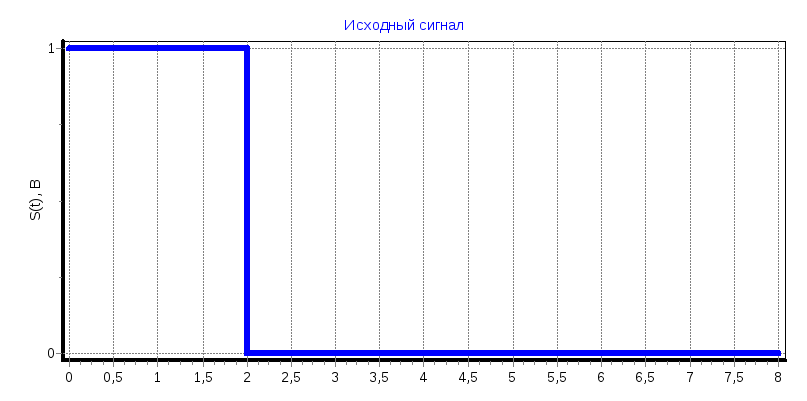
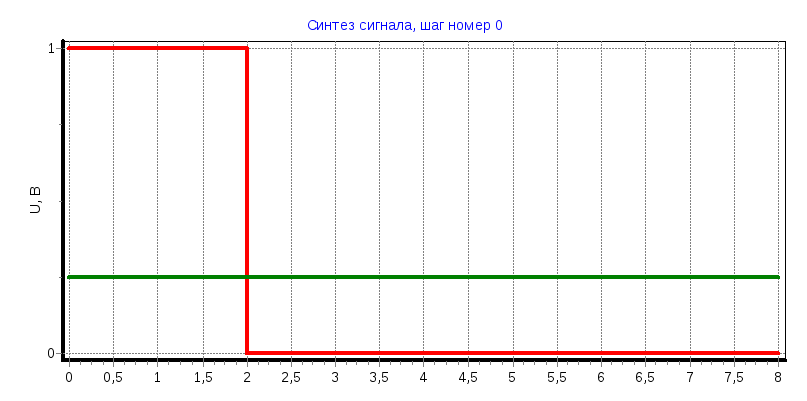
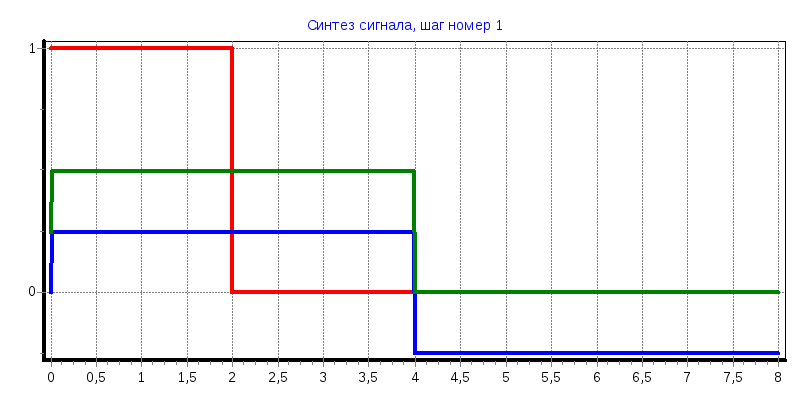
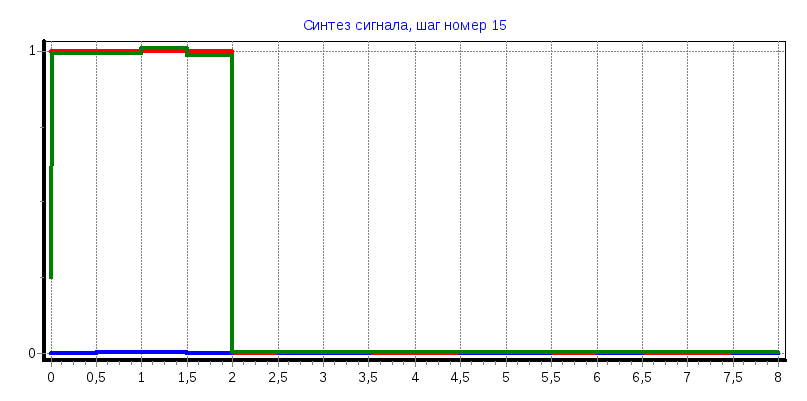
Прямоугольный сигнал

a) t_и=2 мс

С₀ = 0,2495, С₁ = 0,2485, С₂ = 0,2485, С₃ = 0,2485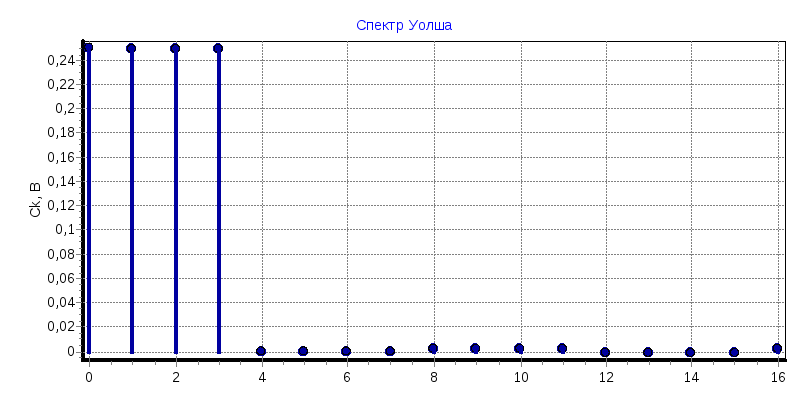

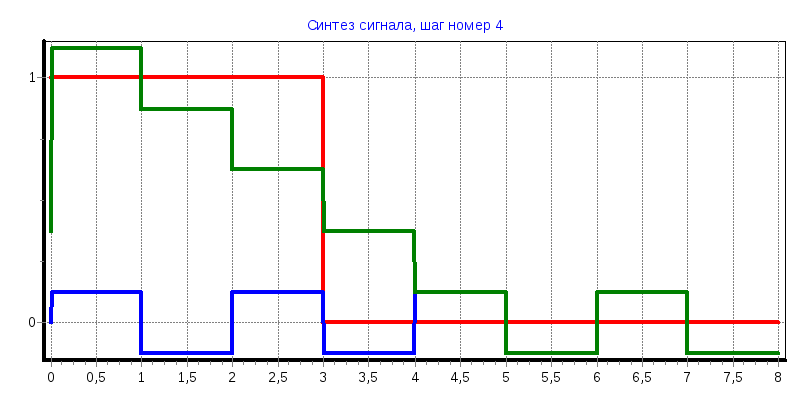
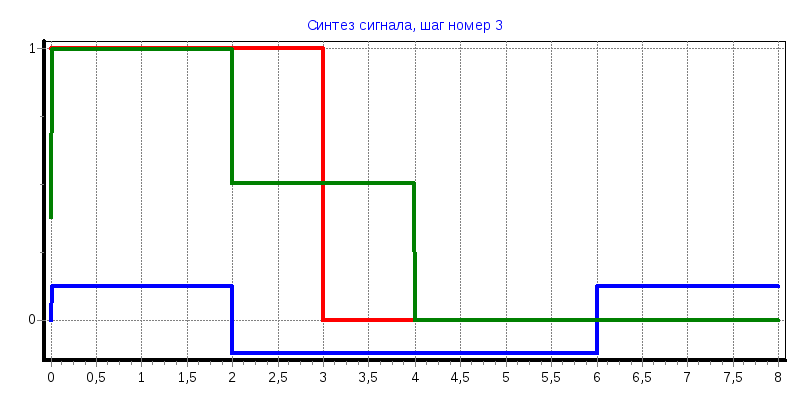
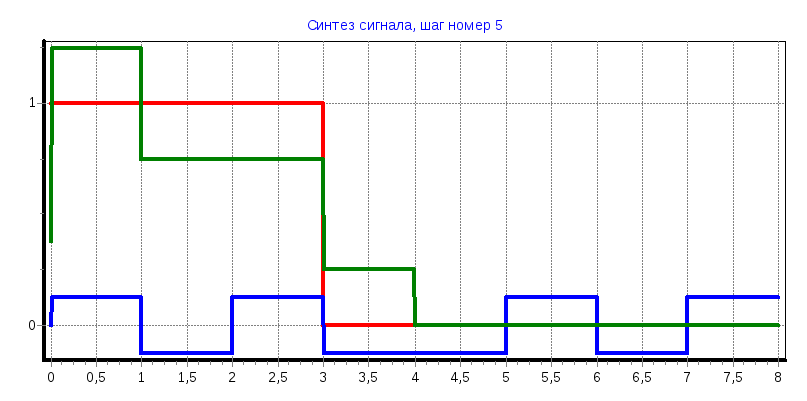
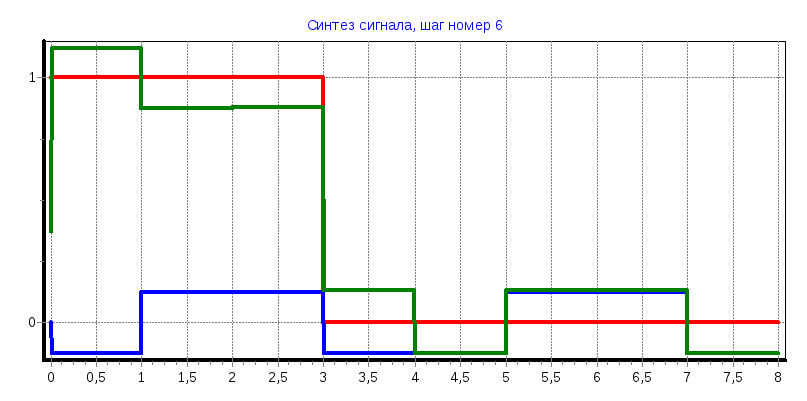
б) t_и=3 мс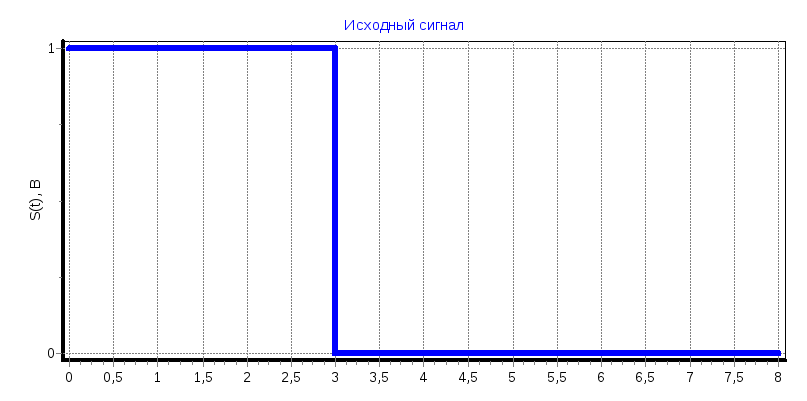

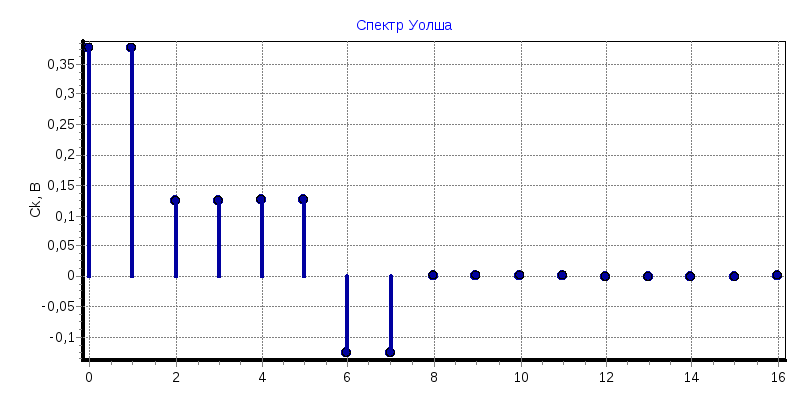
С₀ = 0,3755; С₁ = 0,3745; С₂ = С₃ = 0,1235; С₄ = С₅ = 0,1245; С₆ = С₇ = -0,126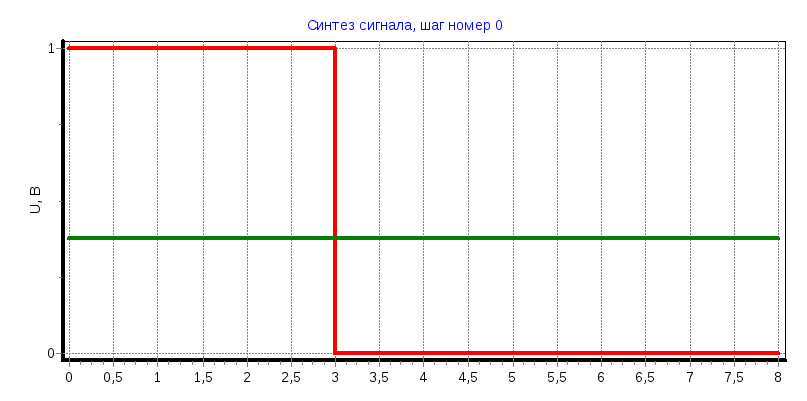

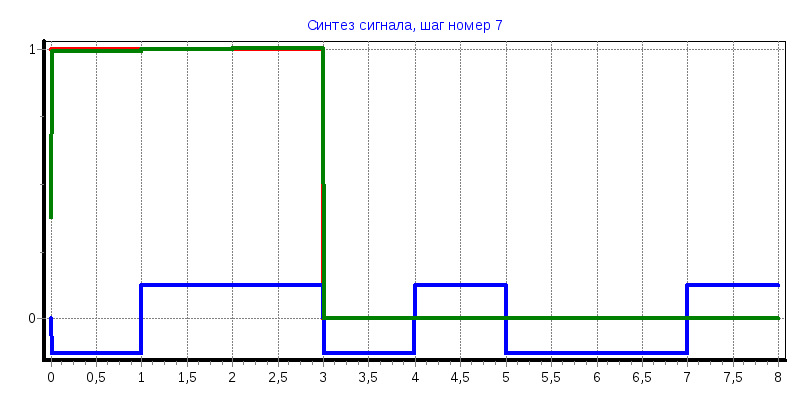
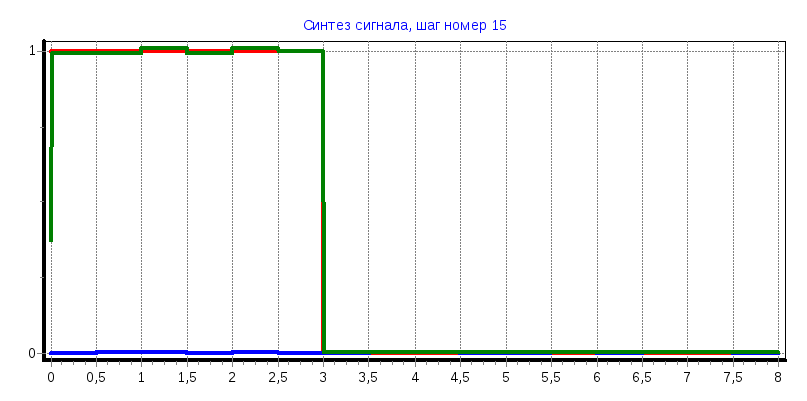
в) t_и=4 мс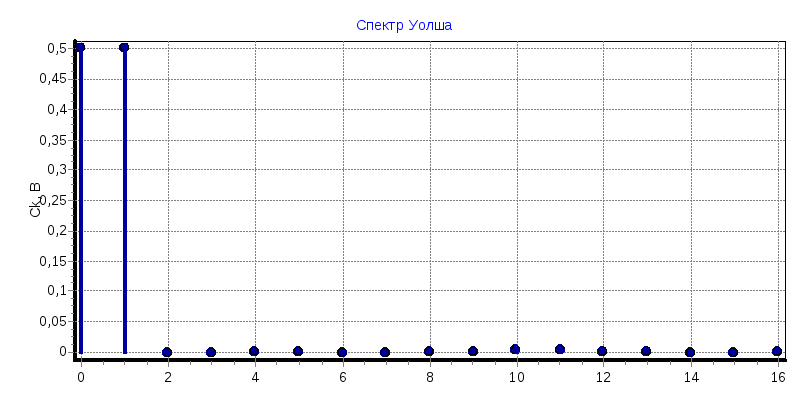

С₀ = 0,5005, С₁ = 0,4995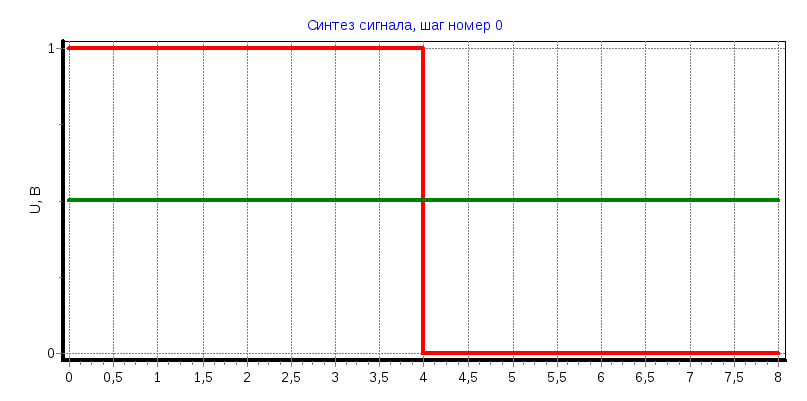

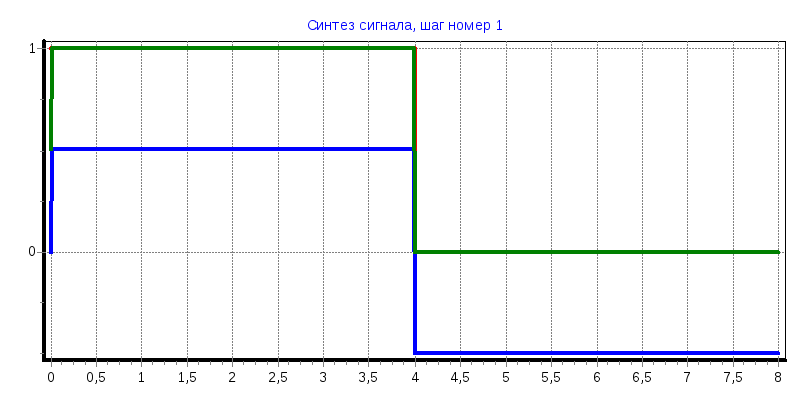
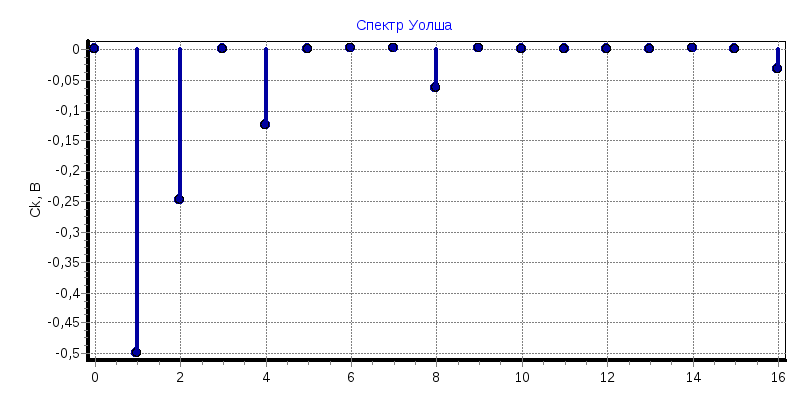
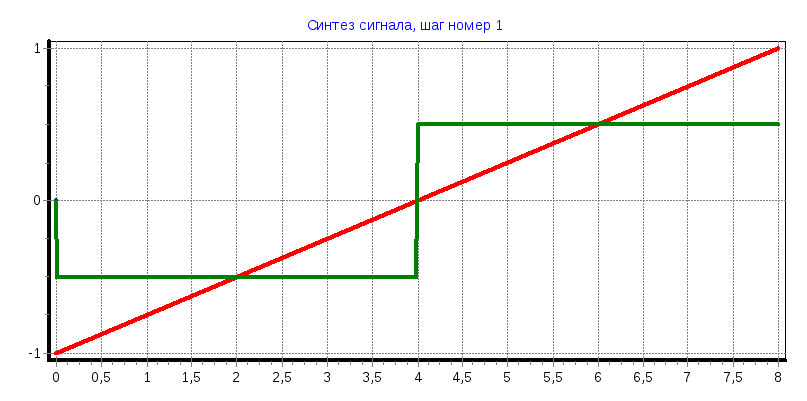
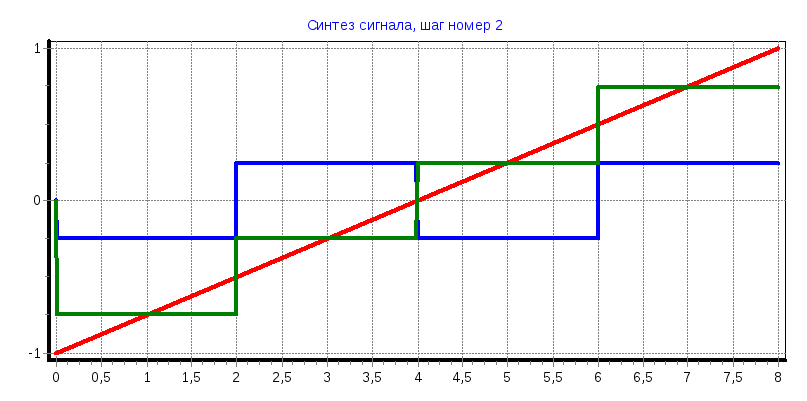
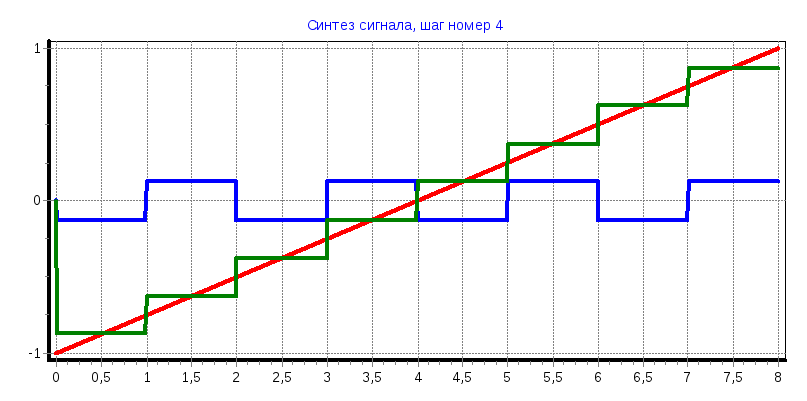
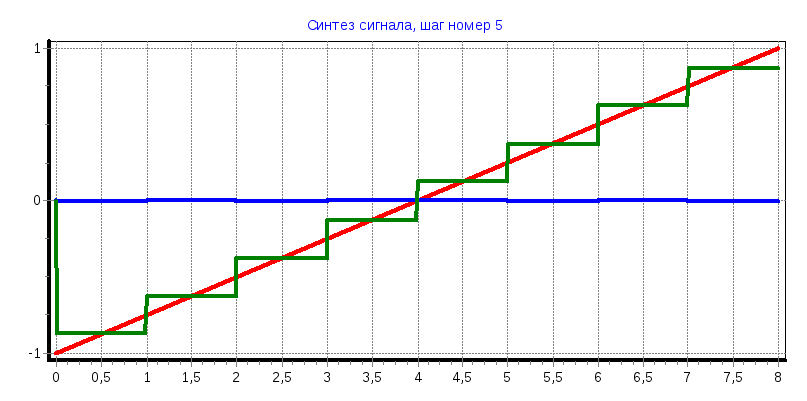
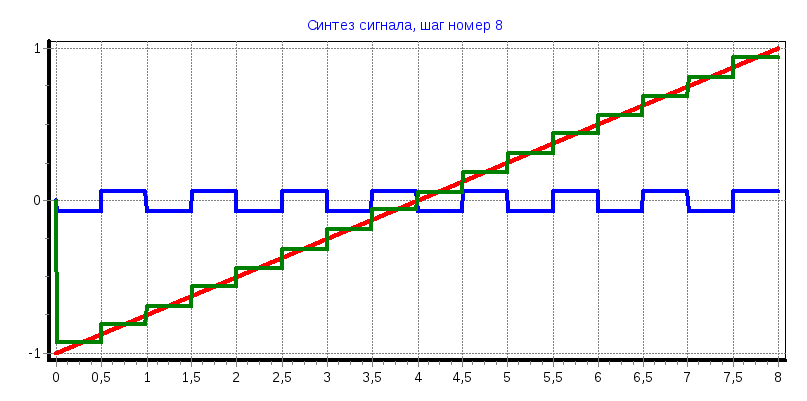
Пилообразный импульс

С₁ = -0,499; С₂ = 0,248; С₄ = -0,123; С₅ = -4,291; С₈ = -0,64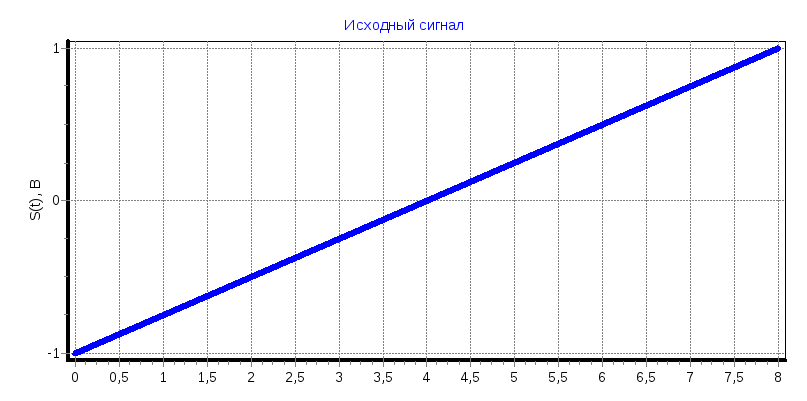

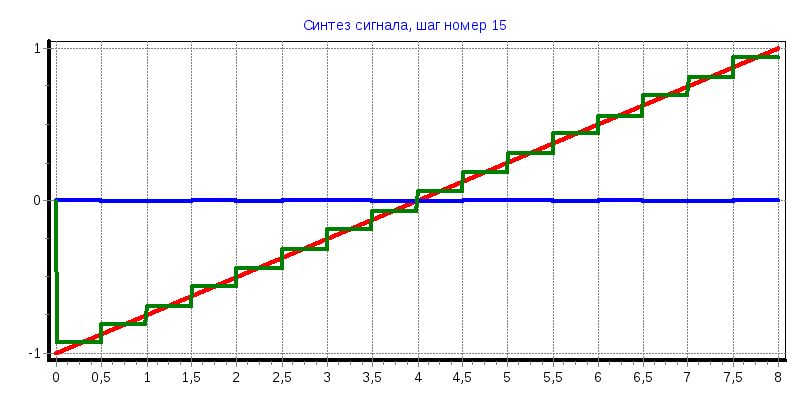
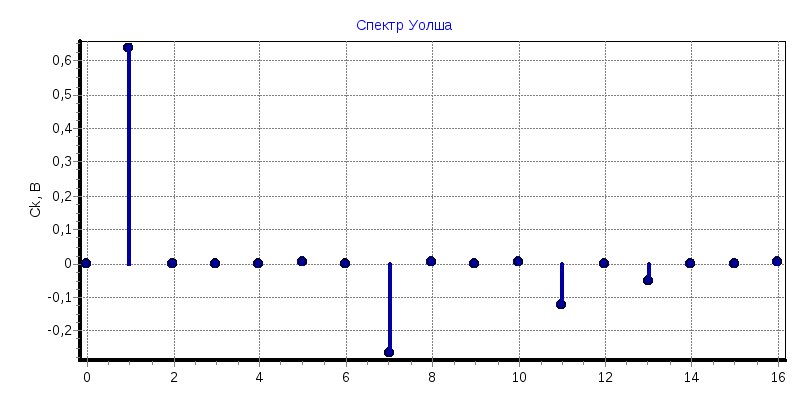
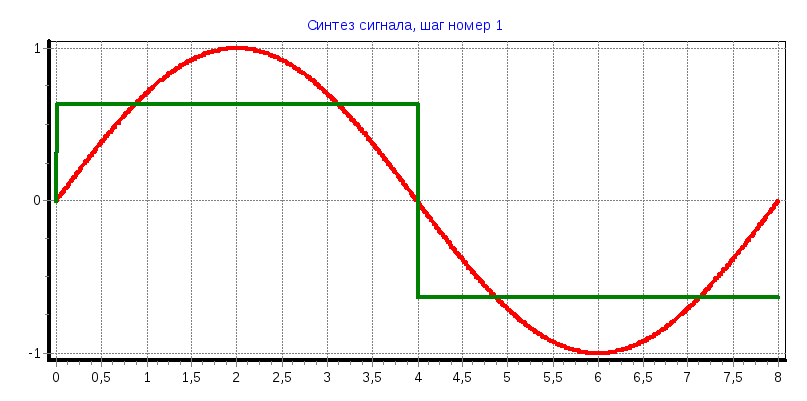
Синусоидальные колебания

а) φ=0°

С₁ = 0,6366; С₇ = -0,265; С₁₁ = -0,125; С₁₃ = -0,052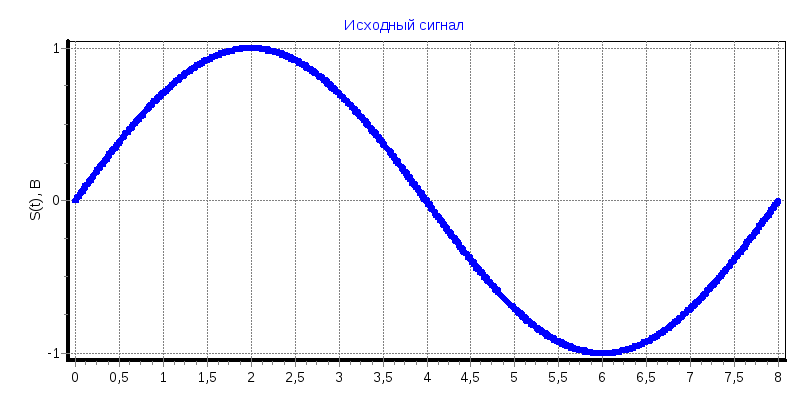

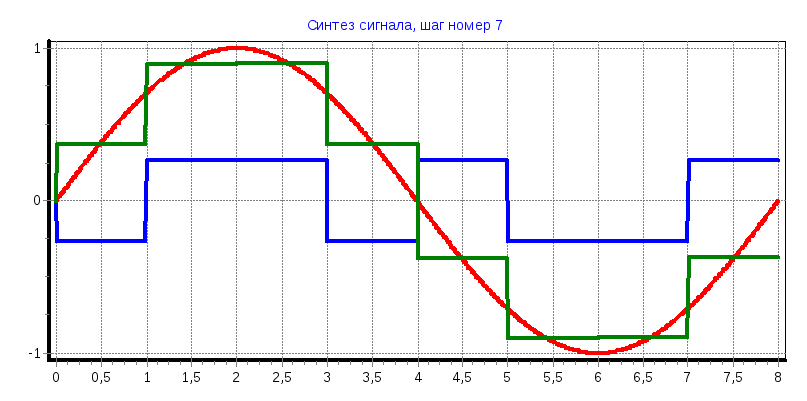
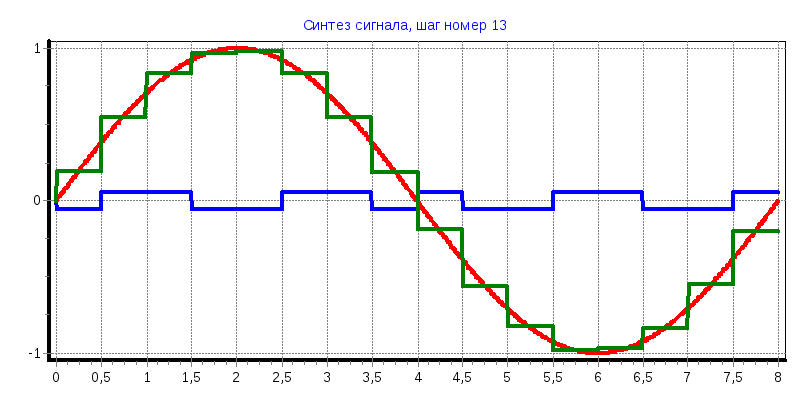
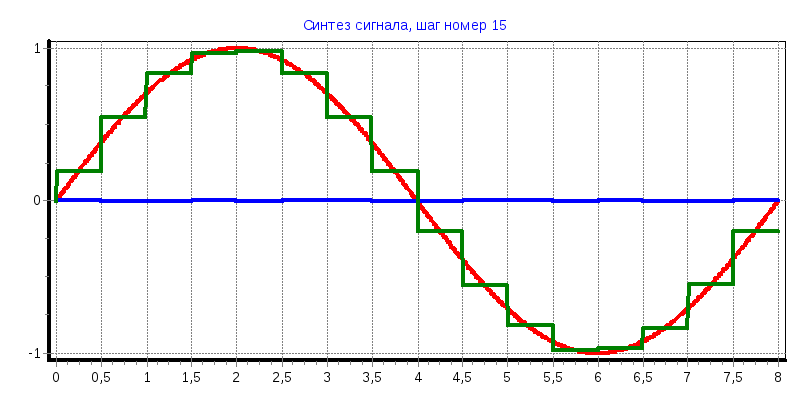
б) φ=45°

С₁ = 0,4991; С₃ = 0,4497; С₅ = 0,1861; С₇ = -0,187;

С₉ = 0,0891; С₁₁ = -0,09;С₁₃ = -0,038; С₁₅ = -0,037

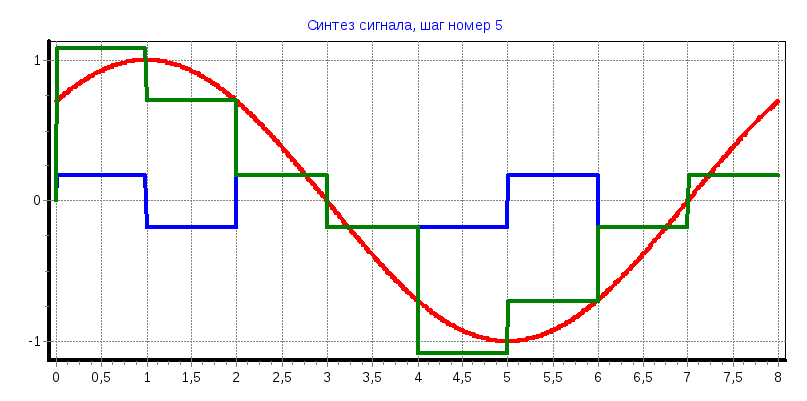
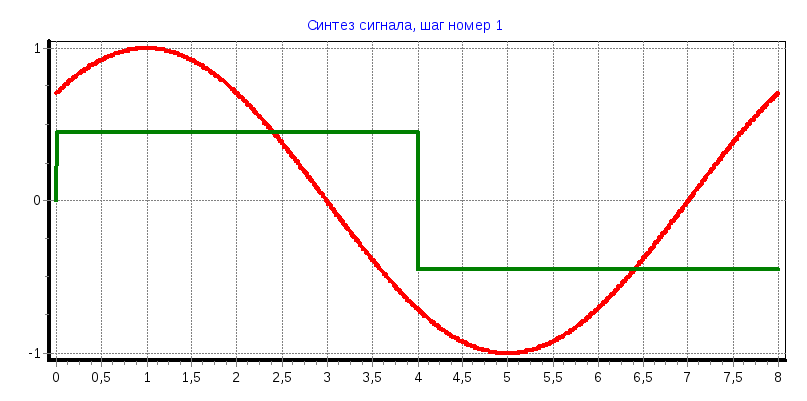
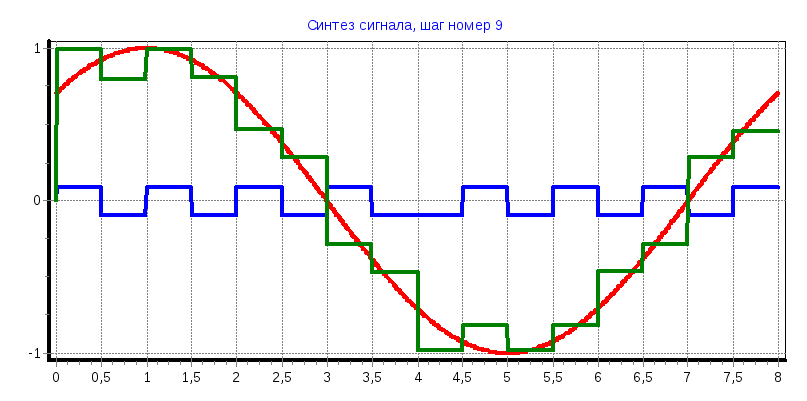
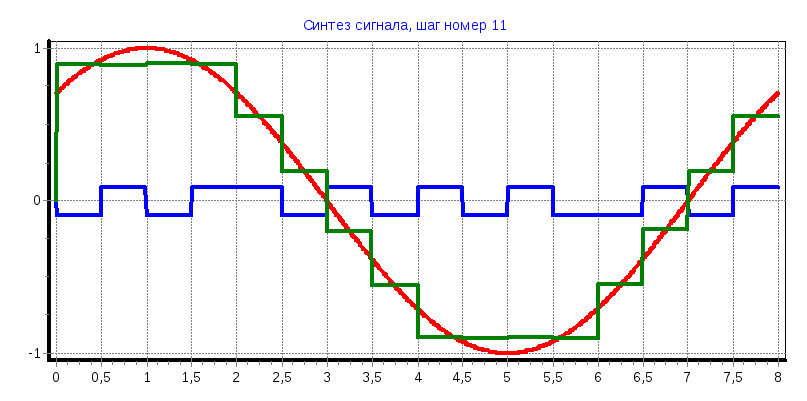
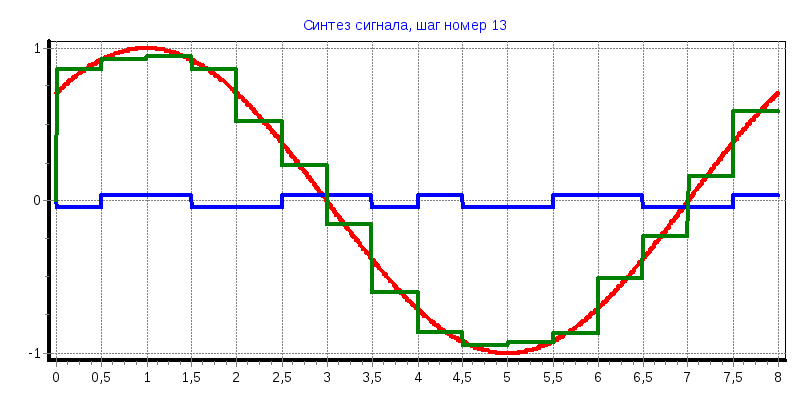
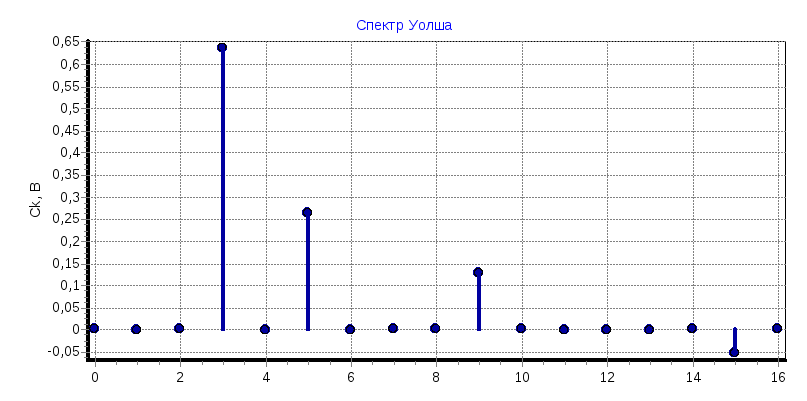
в) φ=90°

С₃ = 0,6361; С₅ = 0,2617; С₉ = 0,1275; С₁₅ = -0,052;

Вывод

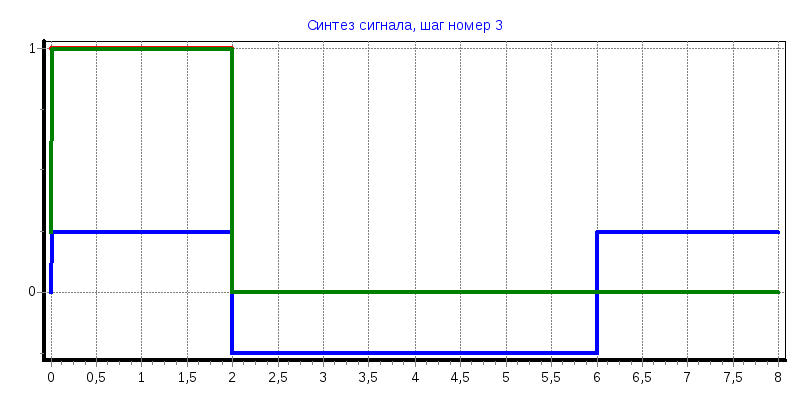
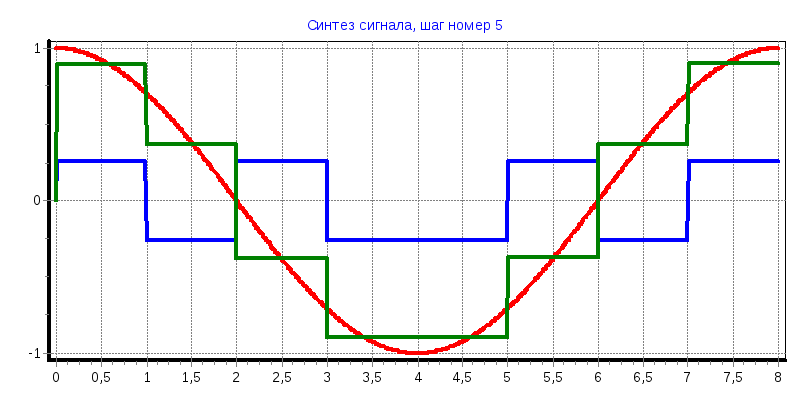
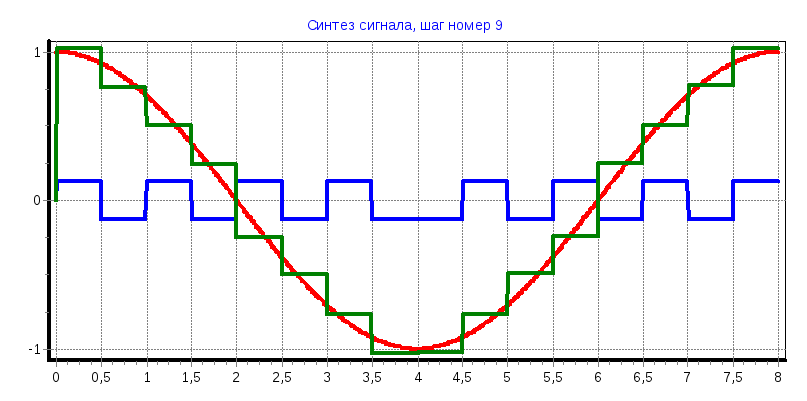
1. При увеличении количества функций Уолша используемых для восстановления исходного сигнала аппроксимированный сигнал приближается к исходному;

2. Синтезированный сигнал имеет ступенчатый вид, что удобно для цифровой обработки сигнала;

3. Функции Уолша универсальны, то есть они применимы для сигнала любой формы (прямоугольного, пилообразного, синусоидального).