Лабораторная работа №2.
Построение регрессионного уравнения с использованием надстройки Поиск решения.
Вариант №13.
Задание.
-
Для набора точек (xi, yi) построить линейную, квадратичную, кубическую и экспоненциальную регрессионную функции и сравнить суммы квадратов остатков для всех функций. Построить диаграммы исходных данных и результатов расчетов по уравнению модели.
|
13 |
X |
-3 |
-2 |
-1 |
0 |
1 |
2 |
|
Y |
-1,70 |
-1,01 |
-0,21 |
0,52 |
0,73 |
1,30 |

-
Поместим исходные данные в диапазон A2:B6.
-
В ячейки A8 и B8 поместим текст – “b0” и “b1”, соответственно, а в ячейки A9 и B9 начальные значения коэффициентов, равные нулю.
-
Вычислим значения yi = b0*xi +b1 для каждой точки. Для этого выделим ячейку C2 и запишем в ней формулу =A$9*A2+B$9.
-
Скопируем формулу вниз до ячейки C6, используя Маркер заполнения (диапазон C2:C6 заполнится нулями).
-
Вычислим остатки для каждой точки. Для этого выделим ячейку D2 и запишем в ней формулу =B2-C2.
-
Скопируем формулу вниз до ячейки D6, используя маркер автозаполнения .
-
Вычислим сумму квадратов остатков. Для этого в ячейку D9 введем формулу =СУММКВ(D2:D6), используя Мастер.
-
Выполним минимизацию суммы квадратов остатков с использованием функции Поиск решения путем изменения A9:B9 без ограничений. Для этого:
-
выполним команду ДАННЫЕ-Поиск решения…;
-
в диалоговом окне Параметры поиска решения установим следующие параметры: целевую функцию - $D$9 (щелкнем по ячейке на рабочем листе); равной – минимальному значению (установим переключатель); в поле Изменяя ячейки переменных введем диапазон $A$9:$B$9 (обведем диапазон на рабочем листе);
-
нажмем кнопку Найти решение.
В диапазоне A9: B9 появятся значения коэффициентов b0 и b1.
Скопируем исходные данные (блок A2:B6) на новый рабочий лист. Для построения уравнения регрессии воспользуемся функцией ЛИНЕЙН(известные_значения_y, известные_значения_x, конст, статистика)
В нашем случае известные_значения_y находятся в диапазоне B2:B6, известные_значения_x – в диапазоне A2:A6. Два последних аргумента логические. Если конст имеет значение ИСТИНА или опущено, то свободный член в регрессионном уравнении может быть любым, а если конст имеет значение ЛОЖЬ, то свободный член принимается равным нулю. Если последний аргумент имеет значение ЛОЖЬ или опущен, то вычисляются только коэффициенты регрессии, в противном случае выдаются дополнительные статистические характеристики. Вместо значений ИСТИНА и ЛОЖЬ можно вводить 1 и 0.
Так как функция возвращает несколько значений, формулу с этой функцией нужно вводить как табличную.
Применение функции
Выделим блок F2:G6. С помощью Мастера функций (категория Статистические) в активную ячейку блока введем формулу =ЛИНЕЙН(B1:B6;A1:A6;1;1) и нажать Ctrl+Shift+Enter. В результате выделенный диапазон заполнится значениями .
В ячейку F2 записан коэффициент b0, в ячейку G2 – коэффициент b1.

Скопируем исходные данные на новый рабочий лист и построим квадратичную регрессию y = b0*x2 +b1*x+b2 с помощью функции линейн.
Для этого в диапазон ячеек F2:H6 введем табличную формулу:
=ЛИНЕЙН(B1:B6;A1:A6^{1;2};1;1)
и нажмем Ctrl+Shift+Enter. В верхней строке диапазона будут записаны значения коэффициентов уравнения.

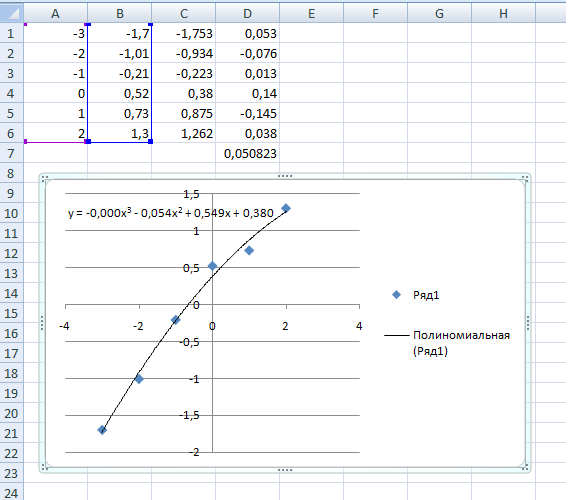
Для заданных исходных данных построим кубическую и экспоненциальную регрессию, добавив Линию тренда (Полиномиальная, степень 3; Линейная; Показывать уравнение на диаграмме).
1.