
системы координат
.rtf2. Системы координат
2.1. Декартова система координат
Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости.
Одна из осей называется осью Ox, или осью абсцисс, другая – осью Oy, или осью ординат. Эти оси называют также координатными осями.
Обозначим через Mx и My соответственно проекции произвольной точки M плоскости на оси Ox и Oy.
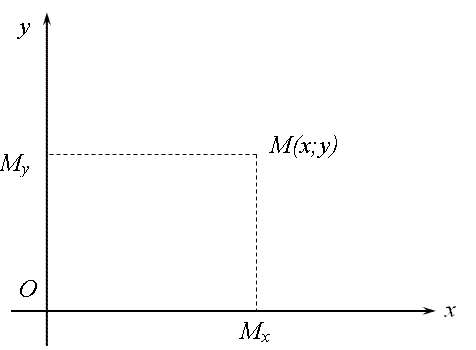
Декартовыми
прямоугольными координатами x и y точки
M
будем называть соответственно величины
направленных отрезков
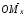 и
и
 :
:
- если
направления
 и Ox
совпадают, то координата x
равна длине
и Ox
совпадают, то координата x
равна длине
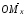 ,
,
- если
противоположны, то x
равна длине
 ,
взятой со знаком «минус». Применяется
обозначение M(x,
y).
,
взятой со знаком «минус». Применяется
обозначение M(x,
y).
Аналогично определяется координата y.
Три взаимно перпендикулярные оси в пространстве с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве.
Одна из осей называется осью Ox, или осью абсцисс, другую – осью Oy, или осью ординат, третья – осью Oz или осью аппликат. Эти оси называют также координатными осями в пространстве.
Декартовы прямоугольные координаты точки в пространстве определяются так же как и на плоскости .
2.2. Полярная система координат
Полярная
система на плоскости задается точкой
О, называемой полюсом,
лучом ОР, называемым полярной
осью
и вектором
 единичной длины и того же направления,
что и луч ОР.
единичной длины и того же направления,
что и луч ОР.

Возьмем на плоскости точку М. Положение точки М определяется двумя числами: её расстоянием r=|ОМ| от полюса О и углом j, образованным отрезком ОМ с полярной осью; при этом отсчет углов ведется в направлении, противоположном движению часовой стрелки.
Числа r, j называются полярными координатами точки М. Пишут М(r; j). При этом r называется полярным радиусом, j – полярным углом. Рассматривают главные значение полярного угла – из полуинтервала [0; 2p). Полярные координаты связаны с прямоугольными следующим образом (на рисунке полярная ось совпадет с осью абсцисс):
полярный
радиус вычисляется по формуле
 ;
;
угол j в зависимости от значений x, y определяется по формулам
j = arctg(y/x), если x > 0, y ³ 0;
j = p – arctg(y/x), если x < 0, y < 0 или x < 0, y ³ 0;
j = 2p + arctg(y/x), если x > 0, y < 0;
j = p/2, если x = 0, y > 0;
j = 3p/2, если x = 0, y < 0.
Для начала координат О r=0, а угол j может быть произвольным.
Если же точка М задана в полярных координатах (r; j), а полярная ось совпадает с осью абсцисс, то
x = r cos j, y = r sin j.
2.3. Представление векторов в декартовой системе координат
Рассмотрим
в пространстве декартову систему
координат Oxyz.
Выделим на координатных осях Оx,
Оy
и Oz
единичные векторы (орты) и обозначим их
 ,
,
 и
и
 .
.

Выберем
произвольный вектор
 и совместим его начало с началом координат
и совместим его начало с началом координат
 =
=
 .
Найдем проекции ax,
ay,
az
вектора
.
Найдем проекции ax,
ay,
az
вектора
 на координатные оси Оx,
Оy
и Oz.
Для этого проведем через конец вектора
на координатные оси Оx,
Оy
и Oz.
Для этого проведем через конец вектора
 плоскости параллельно координатным
плоскостям. Точки пересечения этих
плоскостей с осями координат обозначим
соответственно М1,
М2,
М3.
Получим прямоугольный параллелепипед.
Имеем
плоскости параллельно координатным
плоскостям. Точки пересечения этих
плоскостей с осями координат обозначим
соответственно М1,
М2,
М3.
Получим прямоугольный параллелепипед.
Имеем
 =
= +
+ +
+ .
.
Но
 =
ax
=
ax ,
,
 =
ay
=
ay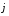 ,
,
 =
az
=
az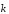 ,
откуда
,
откуда
 =
ax
=
ax +
ay
+
ay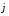 +
az
+
az . (1)
. (1)
Поскольку
векторы
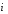 ,
,
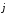 и
и
 некомпланарные, то представление
вектора
некомпланарные, то представление
вектора
 в виде линейной комбинации (1) единственно.
в виде линейной комбинации (1) единственно.
Формула
(1) является основной в векторном
исчислении и называется разложением
вектора по ортам координатных осей.
Числа ax,
ay,
az
называются координатами вектора
 ,
то есть координаты вектора – это его
проекции на соответствующие координатные
оси.
,
то есть координаты вектора – это его
проекции на соответствующие координатные
оси.
Векторное равенство (1) часто записывают в символическом виде:
 =
(ax,
ay,
az).
=
(ax,
ay,
az).
Модуль
вектора
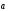 равен
равен

Пусть
углы вектора
 с осями Оx,
Оy
и Oz,
соответственно, равны α,
β и
γ.
Тогда
с осями Оx,
Оy
и Oz,
соответственно, равны α,
β и
γ.
Тогда

Следовательно:

Числа
cosα,
cosβ
и
cosγ
называются
направляющими
косинусами
вектора
 .
Очевидно, что
.
Очевидно, что
сos2α + cos2β + cos2γ = 1.
Пусть
в пространстве задана прямоугольная
декартова система координат Оxyz.
Для любой точки М координаты вектора
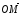 называются координатами точки М.
Вектор
называются координатами точки М.
Вектор
 называется радиус-вектором
точки М, и обозначается
называется радиус-вектором
точки М, и обозначается
 =
=
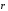 .
Следовательно, координаты точки – это
координаты её радиус-вектора
.
Следовательно, координаты точки – это
координаты её радиус-вектора
 (x,
y,
z)
или
(x,
y,
z)
или
 =
x
=
x +
y
+
y +
z
+
z .
Координаты точки М записываются: М(x,
y,
z).
.
Координаты точки М записываются: М(x,
y,
z).
Даны две точки А(x1, y1, z1) и В(x2, y2, z2). Тогда
 =
=
 =
(x2
–
x1,
y2
–
y1,
z2
–
z1).
=
(x2
–
x1,
y2
–
y1,
z2
–
z1).
Все приведенные выше определения и утверждения, касающиеся представления векторов в координатной форме, справедливы и для векторов на плоскости: в этом случае будут фигурировать не три, а лишь две координаты.
2.4. Действия над векторами в декартовой системе координат
Равенство векторов.
Два
вектора
 и
и
 равны
тогда и только тогда, если
равны
тогда и только тогда, если
 .
.
Линейные операции над векторами.
Пусть
векторы
 =
(ax,
ay,
az)
и
=
(ax,
ay,
az)
и
 =
(bх;
by;
bz)
заданы своими проекциями на оси координат
Оx,
Оy
и Oz:
=
(bх;
by;
bz)
заданы своими проекциями на оси координат
Оx,
Оy
и Oz:
 =
ax
=
ax +
ay
+
ay +
az
+
az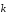 ,
,
 =
bх
=
bх +
by
+
by + bz
+ bz
Операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:
1)
 ±
±
 = (ах
±
bх)
= (ах
±
bх) + (аy
±
by
)
+ (аy
±
by
) + (аz
±
bz)
+ (аz
±
bz)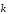
или
 ±
±
 = (ах
±
bх;
аy
± by
; аz
± bz)
= (ах
±
bх;
аy
± by
; аz
± bz)
2)
λ = λax
= λax +
λay
+
λay +
λaz
+
λaz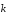 или
λ
или
λ = (λах;
λаy;
λаz)
= (λах;
λаy;
λаz)
Коллинеарность векторов
Теорема
1.
Два заданных вектора
 = (ax,
ay,
az)
и
= (ax,
ay,
az)
и
 = (bх;
by;
bz)
коллинеарные, если найдется такое
действительное число l,
что будет справедливо векторное равенство
= (bх;
by;
bz)
коллинеарные, если найдется такое
действительное число l,
что будет справедливо векторное равенство
 =l
=l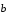 .
При этом число l
определяется единственным образом.
.
При этом число l
определяется единственным образом.
Равенство
 =l
=l можно
представить в виде пропорции
можно
представить в виде пропорции
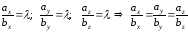
Таким образом проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: два вектора, имеющие пропорциональные координаты, коллинеарны.
Представление скалярного произведения в координатной форме
Даны
два вектора
 =(ax,
ay,
az)
и
=(ax,
ay,
az)
и
 =(bх;
by;
bz).
Их скалярное произведение в координатной
форме:
=(bх;
by;
bz).
Их скалярное произведение в координатной
форме:
( ,
, )
= ax
bх
+
ay
by
+
az
bz
.
)
= ax
bх
+
ay
by
+
az
bz
.
Все приведенные в этом пункте определения и утверждения, справедливы и для векторов на плоскости: в этом случае будут фигурировать не три, а лишь две координаты.
