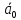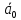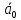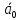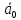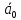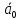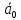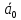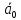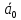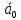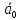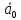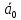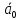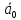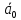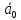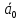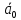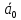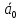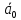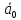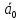Архив1 / docx56 / отчет7(счетчик)

Спроектировать реверсивный двоичный счётчик с самовосстановлением и контролем, имеющий модуль счёта на сложение – М1=11, на вычитание – М2=7.

В качестве элементов памяти используется заданный и спроектированный триггер. Он имеет следующую сокращённую таблицу переходов:

X1	X2	Q(t+1)
0	0	1
0	1	0
1	0
1	1

Определим значения функций возбуждения заданного триггера.

Составим полную таблицу переходов:

№	X1	X2	Qn	Qn+1
0	0	0	0	1
1	0	0	1	1
2	0	1	0	0
3	0	1	1	0
4	1	0	0	0
5	1	0	1	1
6	1	1	0	1
7	1	1	1	0

Из полученной таблицы находим значения функций возбуждения h_X1 и h_X2, которые вызывают переходы триггера a₀, a₁, a₂ и a₃.

hX1	hX2	Переход
0	1	a0
1	0
0	0	a1
1	1
0	1	a2
1	1
0	0	a3
1	0

В результате получаем:

Qn	Qn+1	hХ1	hХ2
0	0	a0
0	1	a1	a1
1	0	—	1
1	1	—	0

Составление обобщённой таблицы переходов счётчика во времени.

Нам задан вариант кодирования М-ричных цифр в коде 5221.

Введем управляющий сигнал V, причем:

1. При V=0 – счётчик работает в режиме сложения.

2. При V=1 - счётчик работает в режиме вычитания.

Тогда обобщённая таблица переходов счётчика во времени будет иметь вид:

№	V	t					t+1					4			3			2			1
		Q4 5	Q3 2	Q2 2	Q1 1	Q4		Q3	Q2	Q1	hx1		hx2	hx1		hx2	hx1		hx2	hx1		hx2
0	0	0	0	0	0	0		0	0	1	a0			a0			a0			a1		a1
1		0	0	0	1	0		0	1	0	a0			a0			a1		a1	—		1
2		0	0	1	0	0		0	1	1	a0			a0			—		0	a1		a1
3		0	0	1	1	0		1	1	0	a0		—	a1		a1	—		0	—		1
4		0	1	1	0	1		0	0	0	a1		a1	—		1	—		1	a0
5		1	0	0	0	1		0	0	1	—		0	a0			a0			a1		a1
6		1	0	0	1	1		0	1	0	—		0	a0			a1		a1	—		1
7		1	0	1	0	1		1	0	1	—		0	a1		a1	—		1	a1		a1
8		1	1	0	1	1		1	1	0	—		0	—		0	a1		a1	—		1
9		1	1	1	0	1		1	1	1	—		0	—		0	—		0	a1		a1
10		1	1	1	1	0		0	0	0	—		1	—		1	—		1	—		1
0	1	0	0	0	0	1		0	0	0	a1		a1	a0			a0			a0
1		0	0	0	1	0		0	0	0	a0			a0			a0			—		1
2		0	0	1	0	0		0	0	1	a0			a0			—		1	a1		a1
3		0	0	1	1	0		0	1	0	a0			a0			—		0	—		1
4		0	1	1	0	0		0	1	1	a0			—		1	—		0	a1		a1
5		1	0	0	0	0		1	1	0	—		1	a1		a1	a1		a1	a0

Используя карты Карно находим минимизированные значения hⁱ_x1 и hⁱ_x2.

hX₁⁴ hX₂⁴

vQ4Q3
100	a1	a0	a0	a0
101				a0
111
110	-
010	-	-		-
011		-	-	-
001				a1
000	a0	a0	a0	a0
	00	01	11	10	Q2Q1

vQ4Q3
100		a1
101
111
110		1
010		0		0			0
011				0		1	0
001							a1
000
		00		01		11	10		Q2Q1

Пусть hX₁⁴=0, тогда a₀=0 (a₀=1) и a₁=0.

hX₂⁴=

hX₁³ hX₂³

vQ4Q3
100	a0	a0	a0	a0
101				-
111
110	a1
010	a0	a0		a1
011		-	-	-
001				-
000	a0	a0	a1	a0
	00	01	11	10	Q2Q1

vQ4Q3
100
101							1
111
110		a1
010							a1
011				0		1	0
001							1
000						a1
		00		01		11	10		Q2Q1