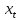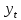Лабораторная работа №7
Решение систем ДУ методом Рунге Кутты
Студента группы ПВ-22
Воробьева Романа Викторовича
Вариант № 3
1.Найти точное решение ДУ системы
Система:
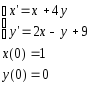
Точное решение:
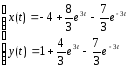
|
t |
|
|
|
0 |
1 |
0 |
|
0.4 |
5,556431621 |
4,7240360692 |
|
0.8 |
25,6068122394 |
15,4858932832 |
|
1.2 |
93,6590472022 |
49,7338905725 |
|
1.6 |
320,0469827931 |
162,9946872819 |
|
2 |
1071,8158997357 |
538,8992742352 |
#include "stdafx.h"
#include <iostream>
using namespace System;
using namespace std;
#define N 2
typedef double* Var;
typedef double (*funct)(Var);
typedef double** matr;
double f0 (double *Var)
{
return Var[1]+4*Var[2];
}
double f1 (double *Var)
{
return 2*Var[1]-Var[2]+9;
}
double* Runge_Kutt(double (**funct)(Var), double Start, int Steps,Var InitArray,double Eps)
{
int i,k,j;
double h,norm,t;
matr C,Vars;
double* Res2;
double* Res1;
double* Res3;
C=(matr) calloc (4,sizeof(double*));
for (i=0; i<4; i++)
C[i]=(double*) calloc (N,sizeof(double));
Vars=(matr) calloc (4,sizeof(double*));
for (i=0; i<4; i++)
Vars[i]=(double*) calloc (N+1,sizeof(double));
Res2=(double*) calloc (N+1,sizeof(double));
Res1=(double*) calloc (N+1,sizeof(double));
Res3=(double*) calloc (N+1,sizeof(double));
h=(Start-InitArray[0]);
t=0;
do
{
norm=0;
Vars[0][0]=t;
for (k=0; k<N; k++)
Vars[0][k+1]=InitArray[k];
while (Vars[0][0]<Start-InitArray[0])
{
for (j=0; j<N; j++)
C[0][j]=h*(funct)[j](Vars[0]);
Vars[1][0]=Vars[0][0]+h/2;
for (k=1; k<N+1; k++)
Vars[1][k]=Vars[0][k]+C[0][k-1]/2;
for (j=0; j<N; j++) C[1][j]=h*(funct)[j](Vars[1]);
Vars[2][0]=Vars[0][0]+h/2;
for (k=1; k<N+1; k++)
Vars[2][k]=Vars[0][k]+C[1][k-1]/2;
for (j=0; j<N; j++) C[2][j]=h*(funct)[j](Vars[2]);
Vars[3][0]=Vars[0][0]+h;
for (k=1; k<N+1; k++)
Vars[3][k]=Vars[0][k]+C[2][k-1];
for (j=0; j<N; j++) C[3][j]=h*(funct)[j](Vars[3]);
for (k=1; k<N+1; k++)
Res2[k]=Vars[0][k]=Vars[0][k]+(C[0][k-1]+2*C[1][k-1]+2*C[2][k-1]+C[3][k-1])/6;
Vars[0][0]+=h;
}
for (i=0; i<N+1; i++)
{
Res3[i]=fabs(Res1[i]-Res2[i]);
Res1[i]=Res2[i];
if (Res3[i]>norm) norm=Res3[i];
}
h/=2;
}while (norm>Eps);
Res1[0]=Start-InitArray[0];
for (i=0; i<4; i++)
{
free(C[i]);
free(Vars[i]);
}
free(C);
free(Vars);
free(Res2);
free(Res3);
return Res1;
}
matr Runge (double (**FunArray)(Var),Var InitArray,double Start,double Finish,int Steps,double Eps)
{
matr Res;
int i;
double h;
Res=(matr) calloc (N+1,sizeof(double*));
for (i=0; i<N+1; i++)
Res[i]=(double*) calloc (Steps+1,sizeof(double));
h=(Finish-Start)/Steps;
Res[0][0]=Start; Res[0][1]=InitArray[0]; Res[0][2]=InitArray[1];
for (i=1; i<Steps+1; i++)
{
Start=InitArray[0]+i*h;
Res[i]=Runge_Kutt(FunArray,Start,Steps,InitArray,Eps);
}
return Res;
}
int main(array<System::String ^> ^args)
{
double Start, Finish,Eps=0.0000001;
funct FunArray[N]={f0, f1};
Start=0; Finish=2;
int Steps=5, i;
matr Res;
double InitArray[N]={1,0};
Res=Runge(FunArray,InitArray,Start,Finish,Steps,Eps);
for (i=0; i<Steps+1; i++)
printf("t= %.3lf x=%.10lf y=%.10lf\n",Res[i][0],Res[i][1],Res[i][2]);
system("pause");
return 0;
}
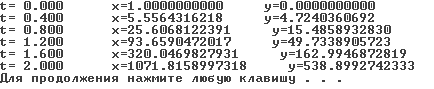
Результат работы программы: