9.1.3.1 Побудова кцп на мультиплексорах
Як приклад роздивимося реалізацію за допомогою восьмивходового мультиплексора (рисунок 9.25) мажоритарного елементу, функціонування якого описано таблицею істинності (таблиця 9.8).
|
N набору |
Х3 |
Х2 |
Х1 |
F |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
1 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
На адресні входи мультиплексора подаються вхідні логічні змінні Х1, Х2, Х3, а на інформаційних входах D0 ... D7 зафіксовані значення реалізованої логічної функції на наборах логічних змінних, номера яких збігаються з номерами інформаційних входів мультиплексора.
Є можливість удвічі скоротити необхідну кількість інформаційних входів мультиплексора (а отже, використовувати більш просту його структуру), якщо на ці входи подати не тільки фіксовані рівні логічних одиниць і нулів, але і значення окремих вхідних змінних Х
Для цього ще раз зобразимо таблицю істинності проектованого мажоритарного елемента, розділивши її на чотири групи по два рядки в кожній (таблиця 9.9).
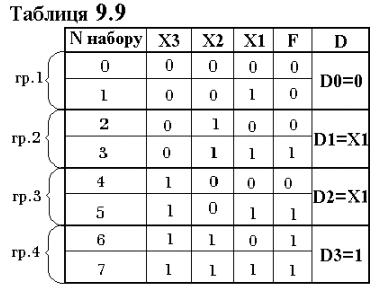
У межах кожної групи можливі тільки чотири значення вихідної булевої функції F: нульове значення на обох наборах - гр.1; одиничне значення на обох наборах - гр.4: збіг функції F із змінною Х1 (набори 2, 3, 4, 5): протилежні значення функції F і змінної Х1 (у даному прикладі відсутні).
Отже, для реалізації відповідного КЦП можна використовувати чотиривходовий мультиплексор, на адресні входи якого подаються змінні Х3 і Х2, а на інформаційні входи D - значення відповідно з останнім стовпчиком таблиці 9.9 (рисунок 9.26).
В результаті є можливість зменшити апаратурні витрати, використовуючи для реалізації тривходового мажоритарного елемента лише половину мікросхеми К555КП2.
9.1.3.2 Побудова кцп на дешифраторах
Для побудови КЦП можна використовувати дешифратори. Завдяки тому що активне значення сигналу на кожному виході дешифратора визначає одну з комбінацій вхідних сигналів, та, об’єднуючи за допомогою відповідних логічних елементів деякі вихідні сигнали дешифратора, можна реалізувати КЦП, задане будь-якою таблицею істинності, із кількістю наборів, що не перевищує кількість входів використовуваного дешифратора. Роздивимося приклад реалізації тривходового мажоритарного елемента (таблиця 9.8) на тривходовому дешифраторі (рисунок 9.27). Якщо використовувати дешифратор з одиничними значеннями вихідних сигналів (рисунок 9.27,а), то вихідний сигнал мажоритарного елемента
F = Y3 Y5 Y6 Y7 . ( 9.16 )
Інверсне значення сигналу на виході мажоритарного елемента
__
F = Y0 Y1 Y2 Y4 . ( 9.17 )
Рисунок 9.27
Після перетворення цього виразу за допомогою теореми де Моргана отримаємо
__ __ __ __
F = Y0 . Y1 . Y2 . Y4. ( 9.18 )
Останній вираз можна використовувати для реалізації мажоритарного елемента на основі тривходового дешифратора з нульовими активними значеннями (рисунок 9.27,б). Якщо порівняти між собою реалізації КЦП на основі мультиплексорів і дешифраторів, то можна відзначити менші апаратні витрати при використанні мультиплексорів. Проте в конкретних умовах проектування КЦП може виявитися доцільним застосування для цих цілей і дешифраторів, наприклад, коли половина мікросхеми здвоєного дешифратора вже використана в складі проектованого пристрою, а інша половина залишилася вільною і може бути застосована для побудови якогось КЦП.