Тема 4. Теорія графів

Питання для самоконтролю

1. Назвіть способи задання графів.

2. Чи можуть від’ємні числа бути елементами матриці суміжності Адеякого графа?

3. Чому дорівнює сума елементів за стовпцем матриці інциденцій деякого графа?

4. Чи дорівнює сума за рядком сумі за стовпцем у матриці суміжності Анеорієнтованого графа? Орієнтованого?

5. Яка кількість компонент зв’язності може бути у графа з nвершинами?

6. Що називають маршрутом у графі?

7. Що називають циклом у графі?

8. Який граф називають повним?

9. Який граф називають доповненням заданого?

10. Який граф називають двоїстим заданому?

11. Назвіть способи обходу графа та наведіть відповідні алгоритми.

12. Який цикл називають ейлеровим? гамільтоновим? Чи будь-який граф є ейлеровим?

13. Яка властивість є достатньою умовою того, щоб довільний граф містив гамільтонів цикл? необхідною умовою?

14. Що називають хроматичним числом графу?

15. Чому дорівнює хроматичне число дерева?

16. Який граф називають деревом?

17. Чи може число ребер дерева дорівнювати числу його вершин?

18. Який граф називають бінарним впорядкованим деревом? Деревом пошуку?

19. Наведіть алгоритми побудови та пошуку для бінарного впорядкованого дерева.

20. Наведіть алгоритми додавання та видалення вузла для бінарного впорядкованого дерева. Який вузол називається термінальним?

21. Що таке бектрекінг і для чого він використовується?

22. Який алгоритм допоможе побудувати дерево прийняття рішень на базі заданого переліку прикладів?

23. Які алгоритми використовуються при побудові остову графа? Чим вони відрізняються?

24. Наведіть алгоритм пошуку мінімального остову графа.

25. Дайте порівняльну характеристику алгоритмів пошуку мінімальних шляхів у графі.

26. Що називають перерізом графу? Сформулюйте теорему про максимальну течію в графі.

27. Дайте порівняльну характеристику алгоритмів пошуку максимальної течії у графі.

Завдання для роботи в аудиторії

Основні поняття

1. Знайти кількість вершин, ребер і степені кожної вершини неорієнтованих графів:

2. Знайти суму степенів вершин кожного з графів задачі 1 та переконатись, що вона вдвічі більша за кількість ребер графа.

3. Визначити кількість вершин та дуг і знайти напівстепені входу й виходу для кожної вершини орієнтованих мультиграфів:

4. Для кожного з графів задачі 3 знайти суму напівстепенів входу та суму напівстепенів виходу вершин. Переконатись, що кожна з них дорівнює кількості дуг графа.

5. Побудувати графи:

a)K₇;b)K_1,8;c)К_1,4;d)С₇;e)W₇;f)Q₄.

6. Які з наведених нижче графів дводольні?

7. Скільки ребер має граф, у якого вершини мають такі степені: 4, 3, 3, 2, 2? Зобразити його.

8. Чи існує простий граф із вершинами таких степенів? Якщо так, то зобразити його:

1. 3, 3, 3, 3, 2;

2. 3, 4, 3, 4, 3;

3. 1, 2, 3, 4, 5;

4. 0, 1, 2, 2, 3;

5. 1, 1, 1, 1, 1.

Способи задання графа

9. Задати графи за допомогою матриць інциденцій та суміжності.

10. Задати графи за допомогою матриць інциденцій та суміжності.

11. Задати прості графи за допомогою матриць інциденцій.

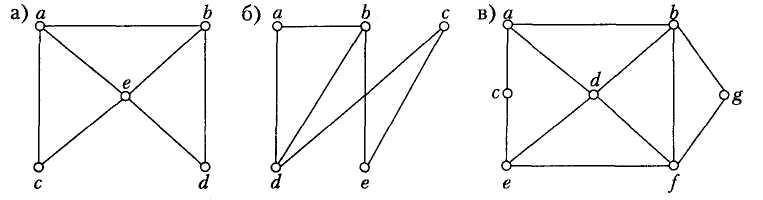
12. Задати графи із задачі 11 за допомогою матриць суміжності.

13. Задати графи задачі 11 списками пар (списками ребер), записаних у лексикографічному порядку.

14. Задати графи задачі 11 списками суміжності.

15. Задати орієнтовані графи за допомогою матриць інциденцій.

16. Задати графи із задачі 15 за допомогою матриць суміжності.

17. Задати графи задачі 15 списками пар (списками дуг), записаних у лексикографічному порядку.

18. Задати графи задачі 15 списками суміжності.

19. Зобразити неорієнтовані графи за матрицями суміжності:

20. Чи є будь-яка квадратна симетрична (0,1)-матриця, що містить 0 на головній діагоналі, матрицею суміжності якогось простого графа?

21. Зобразити орієнтовані графи за матрицями суміжності:

22. Знайти матриці суміжності для графів:

a)K_n;b)С_n;c)W_n;d)K_m,n;e)Q_n.

Операції з графами

23. Простий граф Gмаєnвершин іmребер. Знайти кількість ребер графаG.

24. Побудувати Gдля графів.

25. Визначити, які пари графів, наведених нижче, ізоморфні.

26. Визначити, які пари орієнтованих графів ізоморфні.

Обхід графа

27. Обійти наведені нижче графи пошуком углиб. Вважати, що вершини впорядковано за алфавітом, а початкова — вершина а.

28. Обійти графи із задачі 27 пошуком ушир. Вважати, що вершини впорядковано за алфавітом, а початкова — вершина а.

29. Розв’язати задачі 27 і 28 за умови, що початкова вершина обходу графа - d.

Ейлерові та гамільтонові цикли

30. Знайти точки з’єднання графів.

31. Знайти всі мости в графах задачі 30.

32. Визначити, які з наведених нижче графів мають ейлерів цикл. Зобразити його.

33. Який із графів задачі 32 має ейлерів шлях, але не має ейлеревого циклу?

34. Чи можна утворити ейлерів цикл у разі розміщення мостів?

35. Які з наведених нижче графів мають гамільтонів цикл?

36. Які з графів задачі 35, що не мають гамільтонового циклу, мають гамільтонів шлях?

37. Навести приклад графа, який має ейлерів цикл, але не має гамільтонового циклу, а також графа, який має гамільтонів цикл, але не має ейлерового циклу. Як можна охарактеризувати графи, які мають водночас і ейлерів, і гамільтонів цикли?

Розфарбування графів

38. Оцінити хроматичне число χ(G) графів та розфарбувати їх.

39. Довести, що простий граф, який містить цикл із непарною кількістю вершин, не можна розфарбувати у два кольори.

40. Оцінити хроматичне число графа χ(G) та розфарбувати його.

41. Визначити, які з наведених нижче графів планарні.

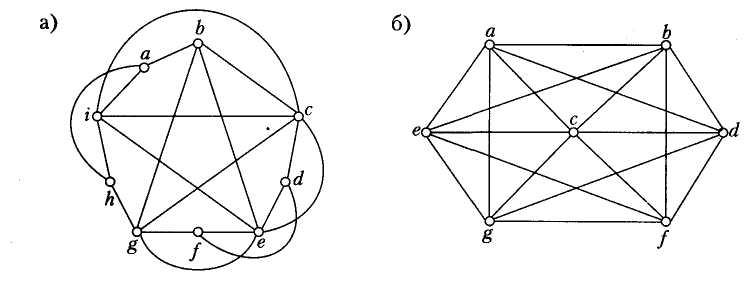
42. За допомогою теореми Куратовського довести, що графи, наведені нижче, непланарні.

43. Зв’язний планарний граф має шість вершин степеня 4. Скільки граней має цей граф?

44. Для планарних графів задачі 41 побудувати двоїсті.

45. Побудувати графи, які відповідають наведеним нижче картам, і визначити найменшу кількість кольорів для їх розфарбовування.

46. Скільки каналів щонайменше потрібно для шести телевізійних станцій, відстані між якими задано таблицею, якщо дві станції не можуть працювати на одному каналі, коли відстані між ними менша ніж 250 км?

Телевізійна станція	1	2	3	4	5	6
1	-	145	280	300	90	160
2	145	-	200	280	150	270
3	280	200	-	220	350	400
4	300	280	220	-	310	360
5	90	150	350	310	-	120
6	160	270	400	360	120	-

47. На кафедрі працюють шість студентських наукових семінарів один раз на місяць в один і той самий час. Скільки різних днів щонайменше потрібно для проведення цих семінарів, якщо склад їх керівників такий:

1) С1 = {Пасічник, Щербина, Чумаков};

2) С2 = {Щербина, Ткач, Катренко};

3) С3 = {Пасічник, Катренко, Чумаков};

4) С4 = {Ткач, Чумаков, Катренко};

5) С5 = {Пасічник, Щербина};

6) С6 = {Щербина, Катренко, Чумаков}.

Умову задачі зобразити у вигляді графа.

Дерева

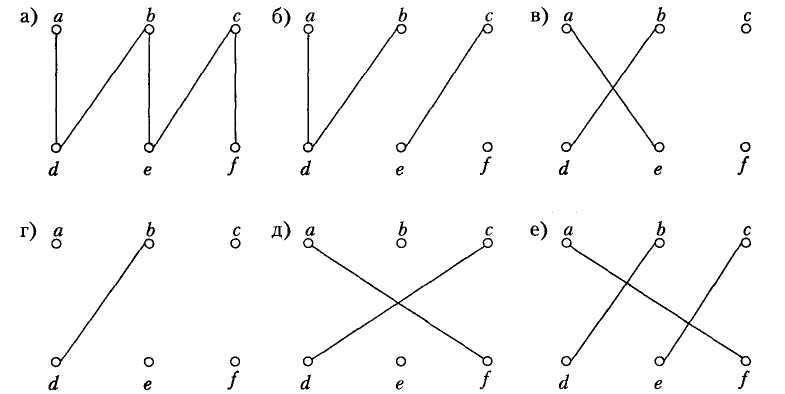
48. Які з наведених нижче графів являють собою дерева?

49. Дати відповідь на запитання щодо дерева, зображеного на рисунку.

1. Яка вершина являє собою корінь?

2. Які вершини внутрішні?

3. Які вершини являють собою листки?

4. Які вершини — сини вершини j?

5. Яка вершина — батько вершини n?

6. Які вершини — предки вершини n?

7. Які вершини — нащадки вершини b?

50. Визначити рівень кожної вершини та висоту дерева з попередньої задачі.

51. У шаховому турнірі беруть участь 1000 гравців. Скільки ігор потрібно зіграти для визначення переможця, якщо турнір проводять за олімпійською системою (той, хто програв, вибуває)?

52. Побудувати завершене бінарне дерево висотою 4 та завершене 3-арне дерево висотою 3.

53. Знайти центри дерев:

54. Довести, що центр у некореневому дереві можна знайти як корінь кореневого дерева з мінімальною висотою.

55. Записати послідовності вершин упорядкованих кореневих дерев, наведених нижче, в разі їх обходу вшир та вглиб.

56. Побудувати бінарне дерево пошуку для чисел {50, 30, 20, 25, 37, 10, 8, 7, 9, 15, 60, 70, 90, 80, 65, 75, 85}.

57. У бінарному дереві попередньої задачі видалити вершини {85, 8, 20}.

58. Побудувати бінарне дерево пошуку для слів {banana,peach,pear,apple,coconut,mango,papaya}.

59. Скільки потрібно порівнянь, щоб знайти чи додати кожне зі слів до дерева пошуку із задачі60:

a) pear, b)banana; c)plum; d)orange.

60. Використовуючи бектрекінг, знайти підмножину (якщо вона існує) множини {27, 24, 19, 14, 11, 8} із зазначеною сумою:

а) 20; b)41; c) 60.

Каркас графа

61. Зв’язний графGмаєnвершин іmребер. Скільки ребер потрібно вилучити з графаG, щоб одержати каркас?

62. Знайти каркас для кожного з наведених нижче графів способом вилучення ребер із простих циклів. Знайти цикломатичне число кожного графа.

63. Для простих графів побудувати всі можливі каркаси.

64. Використовуючи обхід графа пошуком вглиб та вшир, побудувати каркаси для графів, наведених нижче. Як початкову вибрати вершину а.

65. Використовуючи обхід графа пошуком вглиб та вшир, побудувати каркаси для графів, наведених нижче. Як початкову вибрати вершину а.

66. За алгоритмом Краскала для наведених нижче графів побудувати мінімальний та максимальний каркаси.

67. Побудувати мінімальний та максимальний каркаси.

68. Побудувати мінімальний та максимальний каркаси.

69. Побудувати мінімальний та максимальний каркаси.

Найкоротші шляхи у графі

70. За допомогою алгоритму Дейкстри знайти найкоротший шлях відадоz.

71. Знайти найкоротший шлях відадо решти вершин.

72. Знайти найкоротший шлях відадо решти вершин.

73. Знайти найкоротший шлях відадо решти вершин.

74. За допомогою алгоритму Дейкстри знайти найкоротший шлях відадоzв орієнтованому графі.

75. Довести (навести приклад), що алгоритм Дейкстри може й не визначити найкоротший шлях, якщо в графі є дуги з від’ємними довжинами.

76. За допомогою алгоритму Флойда визначити довжини найкоротших шляхів між усіма парами вершин орієнтованого графа. У процесі розв’язування будувати матриціWта Θ. За матрицею Θ визначити найкоротші шляхи від вершиниадо вершиниdта від вершиниbдо вершиниd.

Максимальна течія у графі

77. За допомогою алгоритмуФорда-Фалкерсона знайти максимальну течію між вершинамиатаzу неорієнтованих графах.

78. За допомогою алгоритмуФорда-Фалкерсона знайти максимальну течію між вершинамиатаj.

79. За допомогою алгоритмуФорда-Фалкерсона знайти максимальну течію між вершинамиатаk.

80. За допомогою алгоритмуФорда-Фалкерсона знайти максимальну течію між вершинамиатаc, g, f.

81. За допомогою алгоритмуФорда-Фалкерсона знайти максимальну течію між вершинамиатаzв орієнтованому графі.

Завдання для домашніх робіт

1. Граф задано графічно. Задати його:

   1. списком ребер;

   2. матрицею інциденцій;

   3. матрицею суміжності.

2. Визначити степені вершин графа, кількість компонент зв’язності.

3. Чи є заданий граф повним? планарним?

4. Проаналізувати, чи містить граф

   1. ейлерів цикл або шлях;

   2. гамільтонів цикл або шлях.

5. Знайти G.

6. Побудувати двоїстий граф.

7. Оцінити хроматичне число графа. Розфарбувати вершини графа.

8. Знайти мінімальний каркас графу.

9. Знайти мінімальний шлях між двома заданими вершинами.

10. Знайти максимальну течію між заданими вершинами.

Варіанти завдань

№	G	Знайти шлях між вершинами
		a іg
		b іg
		b іf
		a іh
		b іh
		c іg
		c іh