1.3. Идентификация объекта управления методом моментов
При использовании метода моментов основной проблемой является нахождение функциональной зависимости между моментом входной и выходной функции.
Для
вычисления моментов функции достаточно
знать ее изображение по Лапласу (которое
часто найти гораздо легче, чем функцию).
Действительно, согласно определению
преобразования по Лапласу функции
,
ее изображение:
Равенство (1.3.1) при p=0 имеет вид:
Найдем
значение
при
:
Аналогично, для производных более высокого порядка получим:
Таким
образом, для получения момента любого
порядка некоторой функции
достаточно продифференцировать по
необходимое число раз изображение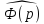
этой функции и положить
.
Получение явных выражений для момента
с помощью выражения (1.3.4) имеет тот
недостаток, что при этом можно получить
только моменты, являющиеся интегралами
по бесконечному промежутку времени.
Итак, передаточная функция описывается уравнением апериодического звена второго порядка. Ее изображение по Лапласу имеет вид:
Тогда выражение (1.3.4) примет вид:
Рассчитаем нулевой момент:
Рассчитаем первый момент (математическое ожидание):
С
другой стороны, т.к. математическое
ожидание – это среднее арифметическое
значений импульсной переходной функции
:
Рассчитаем второй момент (дисперсию):
С
другой стороны, т.к. дисперсия – это
квадрат отклонения значений
от среднего арифметического
:
Итак,
получившаяся система уравнений позволяет
найти
и
,
а следовательно и
и
:
Решение:
Таблица 1.3.1
|
τ |
h(τ) |
k(τ) |
k(τ)*τ |
mx |
(mx-k(τ))^2 |
(k(τ)-mx)^2*τ |
d |
|
0 |
0 |
1,959635 |
0 |
22,03301 |
402,940396 |
0 |
2789,271 |
|
0,375 |
0,734863 |
5,14568 |
1,92963 |
|
285,181926 |
106,9432223 |
|
|
0,75 |
2,664493 |
7,373061 |
5,529796 |
|
214,914112 |
161,1855839 |
|
|
1,125 |
5,429391 |
8,854355 |
9,961149 |
|
173,676966 |
195,3865871 |
|
|
1,5 |
8,749775 |
9,760068 |
14,6401 |
|
150,625116 |
225,9376746 |
|
|
1,875 |
12,4098 |
10,22651 |
19,1747 |
|
139,393561 |
261,3629262 |
|
|
2,25 |
16,24474 |
10,36221 |
23,31497 |
|
136,207569 |
306,4670301 |
|
|
2,625 |
20,13057 |
10,25324 |
26,91475 |
|
138,763067 |
364,2530511 |
|
|
3 |
23,97553 |
9,967455 |
29,90237 |
|
145,577632 |
436,7328969 |
|
|
3,375 |
27,71333 |
9,55807 |
32,25849 |
|
155,624143 |
525,2314835 |
|
|
3,75 |
31,2976 |
9,066489 |
33,99933 |
|
168,130683 |
630,4900605 |
|
|
4,125 |
34,69754 |
8,524656 |
35,16421 |
|
182,475651 |
752,7120602 |
|
|
4,5 |
37,89428 |
7,956949 |
35,80627 |
|
198,135508 |
891,6097846 |
|
|
4,875 |
40,87814 |
7,381724 |
35,9859 |
|
214,660209 |
1046,468518 |
|
|
5,25 |
43,64629 |
6,812558 |
35,76593 |
|
231,662172 |
1216,226404 |
|
|
5,625 |
46,201 |
6,259265 |
35,20836 |
|
248,811066 |
1399,562248 |
|
|
6 |
48,54822 |
5,728702 |
34,37221 |
|
265,830489 |
1594,982937 |
|
|
6,375 |
50,69648 |
5,225431 |
33,31212 |
|
282,494741 |
1800,903975 |
|
|
6,75 |
52,65602 |
4,75224 |
32,07762 |
|
298,625039 |
2015,719011 |
|
|
7,125 |
54,43811 |
4,310564 |
30,71277 |
|
314,085108 |
2237,856394 |
|
|
7,5 |
56,05457 |
3,90082 |
29,25615 |
|
328,776324 |
2465,822433 |
|
|
7,875 |
57,51738 |
3,522671 |
27,74104 |
|
342,63266 |
2698,232201 |
|
|
8,25 |
58,83838 |
3,175236 |
26,1957 |
|
355,615676 |
2933,829325 |
|
|
8,625 |
60,02909 |
2,857251 |
24,64379 |
|
367,709747 |
3171,496572 |
|
|
9 |
61,10056 |
2,567203 |
23,10483 |
|
378,917672 |
3410,259052 |
|
|
9,375 |
62,06326 |
2,303421 |
21,59457 |
|
389,256724 |
3649,281789 |
|
|
9,75 |
62,92705 |
2,064155 |
20,12551 |
|
398,7552 |
3887,863198 |
|
|
10,125 |
63,70111 |
1,847633 |
18,70729 |
|
407,449461 |
4125,425797 |
|
|
10,5 |
64,39397 |
1,652102 |
17,34707 |
|
415,381449 |
4361,505212 |
|
|
10,875 |
65,01351 |
1,475856 |
16,04993 |
|
422,596629 |
4595,738342 |
|
|
11,25 |
65,56695 |
1,31726 |
14,81917 |
|
429,142339 |
4827,851318 |
|
|
11,625 |
66,06092 |
1,174764 |
13,65663 |
|
435,066471 |
5057,647725 |
|
|
12 |
66,50146 |
1,046909 |
12,56291 |
|
440,416452 |
5284,997424 |
|
|
12,375 |
66,89405 |
0,932336 |
11,53766 |
|
445,238479 |
5509,826181 |
|
|
12,75 |
67,24368 |
0,829781 |
10,57971 |
|
449,576958 |
5732,106219 |
|
|
13,125 |
67,55485 |
0,738079 |
9,687288 |
|
453,474115 |
5951,847754 |
|
|
13,5 |
67,83163 |
0,65616 |
8,858161 |
|
456,969742 |
6169,091518 |
|
|
13,875 |
68,07769 |
0,583044 |
8,089739 |
|
460,101062 |
6383,90223 |
|
|
14,25 |
68,29633 |
0,517838 |
7,379189 |
|
462,902665 |
6596,36297 |
|
|
14,625 |
68,49052 |
0,459728 |
6,723524 |
|
465,406522 |
6806,570383 |
|
|
15 |
68,66291 |
4,577528 |
68,66291 |
|
304,693891 |
4570,408363 |
|
|
|
|
|
903,3534 |
|
|
114360,0979 |
|
Расчет в MathCAD:
Рис. 1.3.1. Сравнение исходной функции и полученной в результате метода моментов
Нахождение среднего квадратичного отклонения:
Таблицы 1.3.2
|
τ |
h(τ) |
hm(τ) |
(hm(τ)-h(τ))^2 |
|
|
0 |
0 |
0 |
0 |
|
|
0,75 |
0,957031 |
10,85599 |
97,98943501 |
|
|
1,5 |
3,410596 |
20,02658 |
276,0909641 |
|
|
2,25 |
6,828673 |
27,7737 |
438,6943487 |
|
|
3 |
10,8206 |
34,31855 |
552,1537031 |
|
|
3,75 |
15,10301 |
39,8479 |
612,3097743 |
|
|
4,5 |
19,47362 |
44,51948 |
627,2953299 |
|
|
5,25 |
23,79116 |
48,46651 |
608,8730933 |
|
|
6 |
27,95991 |
51,80148 |
568,4201117 |
|
|
6,75 |
31,918 |
54,61939 |
515,3533169 |
|
|
7,5 |
35,62837 |
57,00051 |
456,7686108 |
|
|
8,25 |
39,072 |
59,01261 |
397,627906 |
|
|
9 |
42,24278 |
60,71294 |
341,1469536 |
|
|
9,75 |
45,14358 |
62,14986 |
289,2135849 |
|
|
10,5 |
47,78341 |
63,36422 |
242,7614418 |
|
|
11,25 |
50,17526 |
64,39053 |
202,0737225 |
|
|
12 |
52,33449 |
65,25793 |
167,0154354 |
|
|
12,75 |
54,2777 |
65,99107 |
137,2029239 |
|
|
13,5 |
56,02194 |
66,61074 |
112,1226348 |
|
|
14,25 |
57,58409 |
67,13453 |
91,21093725 |
|
|
15 |
58,98047 |
67,57728 |
73,90522139 |
|
|
15,75 |
60,22662 |
67,95155 |
59,674529 |
|
|
16,5 |
61,33714 |
68,26794 |
48,03606345 |
|
|
17,25 |
62,32556 |
68,53541 |
38,56229322 |
|
|
18 |
63,20438 |
68,76154 |
30,88204817 |
|
|
18,75 |
63,98502 |
68,95271 |
24,67799399 |
|
|
19,5 |
64,6779 |
69,11435 |
19,68211395 |
|
|
20,25 |
65,29244 |
69,25101 |
15,67027684 |
|
|
21 |
65,83717 |
69,36656 |
12,45657923 |
|
|
21,75 |
66,31977 |
69,46427 |
9,887878843 |
|
|
22,5 |
66,74711 |
69,54689 |
7,838751544 |
|
|
23,25 |
67,12537 |
69,61675 |
6,206983447 |
|
|
24 |
67,46007 |
69,67584 |
4,909631869 |
|
|
24,75 |
67,75612 |
69,7258 |
3,879642096 |
|
|
25,5 |
68,01792 |
69,76805 |
3,062980231 |
|
|
26,25 |
68,24937 |
69,80379 |
2,416229361 |
|
|
27 |
68,45395 |
69,83402 |
1,904591744 |
|
|
27,75 |
68,63474 |
69,85958 |
1,500240464 |
|
|
28,5 |
68,79448 |
69,8812 |
1,180967703 |
|
|
29,25 |
68,9356 |
69,89949 |
0,92908198 |
|
|
30 |
69,06026 |
69,91496 |
0,730512512 |
|
|
|
|
|
Σ= |
7102,319 |
