§4. Плоскости в евклидовом точечном пространстве.

1°. Евклидово точечное пространство.

Определение 1. Аффинное пространство измерений над полем называется –мерным евклидовым точечным пространством, если соответствующее ему векторное пространство есть евклидово пространство.

Из определения 1 следует, что евклидово точечное пространство определяется следующими пятью группами аксиом:

1. Аксиомы сложения векторов (4 аксиомы).

2. Аксиому умножения вектора на число (4 аксиомы).

3. Аксиома размерности.

4. Аксиомы аффинного пространства, связывающие точки с векторами.

5. Аксиомы скалярного произведения.

В евклидовом точечном пространстве вводиться метрика (правило вычисления расстояния между точками). Поэтому становится возможным вычислять площади, объемы, углы,…

Определение 2. Расстоянием между точками и называется длина вектора , т.е. .

Очевидны следующие свойства:

1) – симметричность расстояния.

2) .

3) – неравенство треугольника.

В аффинном пространстве базис определяется репером , где . Если базис – ортонормированный, то репер называется ортонормированным, и расстояние между точками и : определяется формулой . Если репер произвольный, то расстояние вычисляется с использованием матрицы Грама.

2°. Вектора, ортогональные плоскости в евклидовом точечном пространстве.

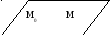
Рассмотрим –мерную плоскость заданную уравнениями

(1)

Определение 3. Будем говорить, что вектор E ортогонален плоскости (1), если ,.

Из определения 3 видно, что множество всех , ортогональных плоскости , есть ортогональное дополнение к направляющему пространству плоскости (1),

Иногда называют ортогональным подпространством –мерной плоскости .

Пусть базис образован векторами . Найдём скалярные произведения (1) на эти вектора:

.

(2)

Пусть в E введён ортогональный базис. Тогда левые части уравнений системы (2) – линейные функции от , а правые – числа, т.е. (2) – система линейных неоднородных уравнений на . Ранг матрицы системы равен . Множество всех решений образует плоскость .

Таким образом, справедливо

Утверждение 1. Если в евклидовом точечном пространстве с ортонормированным базисом, плоскость задана СЛНУ, то коэффициенты системы являются координатами векторов нормального подпространства к плоскости . Размерность нормального подпространства равна рангу системы.

В случае гиперплоскости нормальное подпространство одномерное. Пусть оно определяется вектором . Тогда следуя (2) уравнение гиперплоскости может быть задано в виде

.

(3)

Таким образом, точка принадлежит гиперплоскости (3) вектор .

Для задания гиперплоскости в виде (3) достаточно знать вектор , ортогональный гиперплоскости, и точку .

3°. Расстояние от вектора до подпространства.

Рассмотрим евклидово пространство E и пусть E.

Определение 4. Расстоянием между векторами E назовём величину

.

(4)

Из свойств евклидова пространства следует, что

.

(5)

Если рассматривать как стороны треугольника, то – третья сторона треугольника.

Если треугольник прямоугольный, т.е. , то

(6)

– теорема Пифагора. Из формулы (5) в силу

, , т.е.

, .

(7)

Таким образом, в евклидовом пространстве длина стороны треугольника не превосходит суммы длин двух других его сторон, но не меньше их разности.

Из (4) следует, что введённое в определение 4 понятие расстояние удовлетворяет обычным свойствам расстояния (метрики):

1. 

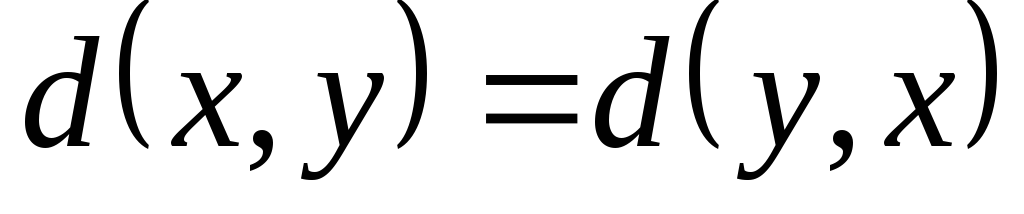
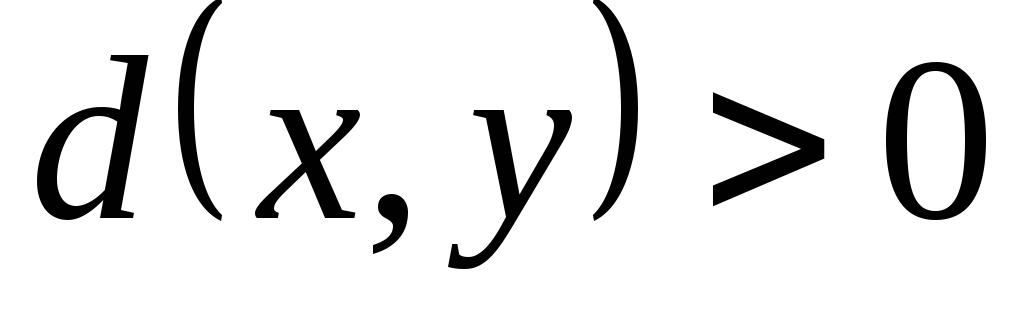2. и

3. 

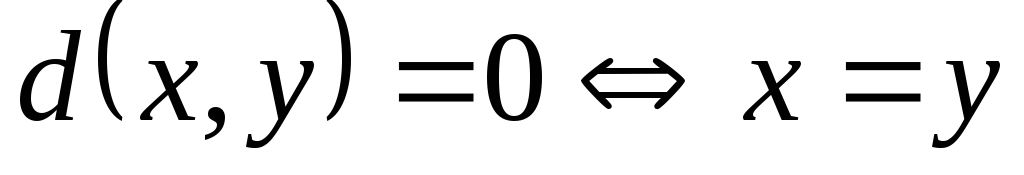
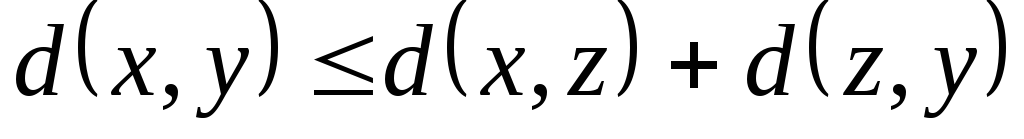
Первые два свойства очевидны, а третье следует из (7), если , .

Определение 5. Если – множества векторов, то расстояние между называются величина

.

Теперь в евклидовом пространстве E фиксируем подпространство и пусть – произвольный вектор из E.

Известно, что для пространства однозначно определённое ортогональное дополнение и вектор однозначно может быть представлен в виде

(8)

где , .

Определение 6. В таком рассмотрении называется проекцией на , –перпендикуляром, опущенным из на , а сам вектор – наклонной к подпространству .

Т.к. векторы – перпендикулярны по теореме Пифагора , т.е. длина перпендикуляра не превосходит длины наклонной и длина перпендикуляра равна длине наклонной .

Задаче о перпендикуляре можно дать другую трактовку. Пусть и надо найти вектор в : он ближе всего расположен к в смысле определения 4. Пусть вычитая его из (8), имеем , так как по теореме Пифагора

причём это равенство дополняется лишь только если .

Итак,

Утверждение 2. Среди всех векторов из подпространства проекция вектора на . Ближе всего расположена к , т.е. .

Углом между вектором и подпространством E называется наименьший из углов между и векторами .

Известно, что

Причём равенство получается, если .

Таким образом, угол между и равен углу и проекцией на . Если ввести обозначения , , т.е. в силу условия , имеем , .

В силу единственности представления имеем , .

4°. Расстояние от точки до плоскости

Пусть в аффинном пространстве Азадана плоскость , проходящая через точку в направлении подпространства , и точка . Тогда вектор может быть представлен в виде

,

где , .

Определение 7. Расстоянием от точки до плоскости будем называть величину

.

Из свойств, рассматриваемых в 2°, что определённое таким образом расстояние от до плоскости есть минимальное расстояние от до точки плоскости.

Домашнее задание: показать, что, то определение корректно, т.е. не зависит от выбора точки на плоскости.

5°. Нормальное уравнение гиперплоскости в евклидовом пространстве.

Пусть в E задана система координат с произвольным ортонормированным базисом и в этой системе координат задано уравнение гиперплоскости

(9)

где – нормаль гиперплоскости.

Если уравнение (9) , а , то уравнение называется нормальным уравнением гиперплоскости.

Определение 8. Уравнение

(10)

где , , называется нормальным уравнением гиперплоскости.

Чтобы привести (9) к нормальному виду, достаточно умножить его на нормирующий множитель

выбрав знак так, что . Тогда (если , то берут со знаком +).

Отметим, что координаты – направляющие косинусы.

Пусть – радиус вектор текущей точки E плоскости. Тогда

(11)

– угол между и . Т.е., есть проекция вектора на нормаль с положительными направляющими . Вместе с тем, не трудно видеть, что есть расстояние от начала координат до гиперплоскости. Действительно, из (11) и , если . Таким образом, есть длина самого короткого из радиус–векторов, имеющих концы на плоскости (см. рисунок).

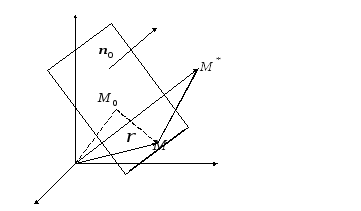
Пусть – радиус–вектор точки , не лежащей на плоскости . Рассмотрим .

Имеем

и – длина самого короткого из этих векторов – расстояние от до плоскости. Знак таков, что , если и лежат по одну сторону от плоскости и – если по разные.

Таким образом, гиперплоскость делит пространство на два полупространства, если

,

то это отрицательное полупространство (содержит начало координат) и

– положительное полупространство.

Задача. Найти расстояние от точки до плоскости .

Решение. .