3.5. Поняття індуктивності. Енергія магнітного поля постійного

струму

Нагадаємо, якій елемент електричного кола здатен накопичувати магнітну енергію. Цей елемент – котушка індуктивності, або соленоїд (дросель). Відомо, що основний функціональний параметр соленоїда – індуктивність.

Індуктивність – властивість фізичних об’єктів накопичувати та віддавати енергію магнітного поля визначають, як відношення магнітного потоку Ф до сили струму І, який цей потік створює.

_Тобто (3.70)

За одиницю індуктивності прийнято індуктивність такого контуру, магнітний потік самоіндукції якого за силу струму в 1 А дорівнює 1 Вб. Ця одиниця має назву генрі (Гн): 1 Гн = 1 Вб/А= 1 В∙с/А=1 с∙Ом.

Визначимо індуктивність дроселя за формулою (3.70) з урахуванням, що дросель маєвитків, тобто замість Ф застосуємо потокозчеплення 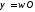та у формулу закону повного струму сумарну силу струму, який протікає в дроселі записуємо, якwI.

Отже, наведемо низку перетворень:

,(3.71)

де S – перерізосердя магнітопроводу, l – довжина середньої лініі

Для змінення магнітного потоку за значенням необхідно виконати роботу

(3.72)

Інтегруванням цього рівняння, отримаємо формулу роботи, яку необхідно виконати для створення магнітного поля:

(3.73)

Тобто енергія магнітного поля:

.(3.73а)

Енергію магнітного поля можна також навести, як функцію величин, що характеризують це поле: H. B.

Проаналізуємо однорідне магнітне поле всередині соленоїда (дроселя) з індуктивністю за формулами (3.70) і (3.71), й отримаємо

, (3.74)

де – об’єм соленоїда.

Або узагальнено

. (3.75)

3.6. Висновки

1. Протікання у провіднику постійного струму створює навколо нього магнітне поле.

2. Проявом магнітного поля є сила взаємодії умовних магнітних зарядів , [Н].

3. Для використання співвідношень отриманих в електростатиці розроблено модель магнітного стрижня (спиці) із зосередженим на кінцях умовними магнітними зарядами , [B∙с].

4. Для визначення магнітного характеру сили взаємодії рухомих зарядів введено поняття вектор напруженості магнітного поля ,– це силова характеристика поля.

5. Для визначення характеристик магнітного поля, незалежно від параметрів середовища застосовують поняття вектор магнітної індукції

,.

6. Для опису характеристик магнітного поля застосовують поняття – потік вектора магнітної індукції, циркуляція вектора напруженості магнітного поля, дивергенція та ротор.

7. Співвідношення між напруженістю магнітного поля та його джерелом, електричним струмом, визначає закон Біо-Савара.

8. Магнітне поле має вихровий характер, тому потік вектора та дивергенція магнітної індукції дорівнюють нулю ,.

9. Для визначення характеристик магнітного поля, яке створює струм в реальних провідниках застосовують закон повного струму (круговий закон Ампера) – в інтегральній, та– диференціальній формах.

10. Для розв’язку деяких задач магнітного поля постійного струму та електродинаміки є зручним перетворення (теорема) Стокса: .

11. Допоміжною характеристикою магнітного поля є векторний магнітний потенціал .

12. Векторний магнітний потенціал визначають із розв’язку аналога рівняння Пуассона , звідки.

13. За умов існування магнітного поля у просторі, параметри якого різні, вимагає розгляду граничних умов:

– для нормальних складників використовують потік вектора , (),

– для тангенціальних складників використовують циркуляцію вектора ,

– ().

14. Практичне значення має ситуація, коли одне із середовищ є ідеальним провідником. В цьому випадку силові лінії вектора паралельні (дотичні) до провідної поверхні.

15. Індуктивність – це фізична величина, яка характеризує взаємозв’язок між магнітним потоком та силою струму, який створює це поле; її математична модель .

16. Енергію магнітного поля визначають через індуктивність, силу струму, та характеристики поля: ,.