3.4. Граничні умови магнітного поля постійного струму

Використаємо аналогічний підхід як в електростатиці. Для нормальних складників скористаємось формулами потоку вектора магнітної індукції, для тангенціальних – циркуляцією напруженості магнітного поля, як це застосовано в 2.7.

3.4.1. Нормальні складники векторів та

Нормальний складник вектора – проекція вектора на нормаль до межі розподілу. Нехай вектор перетинає межу поділу двох середовищ. Виділимо нескінченно малу ділянку поверхні, щоб можна було нехтувати її кривизною та вважати значення незмінним, іconst.

Побудуємо циліндр з поперечним перерізом , твірні якого паралельні до нормалі(рис. 3.7).

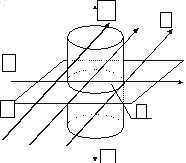
Рисунок 3.7. До визначення нормальних складників магнітного поля

Магнітні заряди існують як диполь. Тому сумарний магнітний заряд 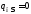, а отже аналог закону Гаусса для магнітного поля такий:

(3.57)

Потік вектора – це сума потоків

(3.58)

Оскільки заряд зосереджено на площадці ,то без втрати загального результату можна спрямувати до нуля висоту циліндра, тобто і площу бічної поверхні. Тоді

(3.59)

Перший доданок характеризує стан в першому середовищі, а другий в другому. Зменшуємо так, щоб можна було вважати, що в кожній точцітоді:

(3.60)

За умови , то з (3.60) маємо скалярні добутки:

(3.61)

Складники лівої частини рівняння є нормальними складниками вектора магнітної індукції.

(3.62)

Тобто (3.62а)

Для напруженості магнітного поля:

(3.63)

(3.63а)

3.4.2. Тангенціальні складники векторів та

Для визначення тангенціального складника зручним є вибір вектора .

Нехай вектор напруженості магнітного поля перетинає межу двох середовищ. Визначимо циркуляцію вектора за контуром(рис. 3.8). Поняття циркуляції зручно застосовувати, адже циркуляція не залежить від форми контуру, тому виберемо для зручності контур прямокутної форми, сторони якого нескінченно малі, а напрям обходу за годинниковою стрілкою (рис. 3.8).Циркуляція характеризує роботу сил поля. За визначенням для магнітного поля ,

тобто:

(3.64)

Рисунок 3.8. До визначення тангенціальних складників магнітного поля

Якщо наближати контур до межі, то інтеграли дорівнюють нулю. Тоді із (3.64) маємо

(3.65)

Перший доданок характеризує перше середовище, другий –друге. Сторони ab та cd , відповідно нескінченно малі величини і дорівнюють , тому можна вважати, що в кожній точці, тоді:

(3.66)

З (3.65) з урахуванням (3.66) та напрямків обходу контурів отримаємо:

.

Із урахуванням, що ab=cd= та після скорочення маємо:

. (3.67)

Тобто

, (3.68)

або

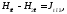(3.69)

де – поверхнева густина струму провідності вздовж границі розподілу, А/м.

3.4.3. Граничні умови на поверхні ідеального провідника

Для тангенціальних складників з формули (3.69) за умови, що всередині ідеального провідника сумарне поле відсутнє, маємо:

,

тобто на межі розподілу існує лише дотичний складник вектора напруженості магнітного поля.

Нормальний складник вектора напруженості магнітного поля, як випливає з (3.64) та (3.65), із урахуванням, що всередині провідника магнітне Н відсутнє:

.

Отже, силові лінії магнітного поля на границі розподілу середовищ зорієнтовані лише вздовж дотичної до поверхні провідника (табл. 3.1), тоді як силові лінії електричного поля спрямовані перпендикулярно до провідника (табл. 2.1).

Таблиця 3.1. Граничні умови магнітного поля постійного струму

Складник поля	Базові співвідношення	Граничні умови
		У загальній формі	З ідеальним провідником
Нормальний n
Тангенціальний τ