3.2.3. Перетворення (теорема) Стокса

З’ясуємо взаємозв’язок сумарного струму в контурііз густиною струмів.

Перетворення Стокса пов’язує інтеграли різного порядку (на зразок перетворення (теореми) Гаусса –Остроградського). Це дозволяє переходити від лінійного інтеграла до поверхневого, і навпаки, що в деяких ситуаціях суттєво полегшує розв’язування задач електродинаміки.

Скористаємось підходом аналогічно п. 2.3.3 для перетворення Гаусcа – Остроградського. Розгляд почнемо зі струму та скористаємось відомими формулами:

,

. (3.39)

Отже отримаємо:

(3.40)

Тобто циркуляція вектора за довільним замкненим контуром дорівнює потоку його ротора через поверхню, обмежену цим контуром. Таким чином співвідношення (3.40) пов’язує лінійний інтеграл з поверхневим, що дозволяє змінювати порядок інтегрування.

3.3. Розв’язування прямої задачі магнітного поля постійного струму у загальній формі

Як встановлено вище, першопричиною магнітного поля є струм:

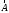
де – визначає силовий вплив, тобто напруженість магнітного поля, – густину потоку, є допоміжний параметр– векторний магнітний потенціал.

Встановимо зв’язок між густиною струму та напруженістюмагнітного поля створеного струмом.

Вектор визначають трьома проекціями, тому для розв’язання цієї задачі знадобиться система не менш, як із трьох рівнянь.

Перше рівняння – закон повного струму в диференціальній формі:

. (3.41)

Магнітне поле існує у певному середовищі, яке характеризується магнітною проникністю, тому друге рівняння це:

– друге матеріальне рівняння середовища. (3.42)

Третє рівняння – аналог закону Гаусса – Остроградського в інтегральній формі, стосовно магнітних тіл:

, (3.43)

тобто потік вектора магнітної індукції дорівнює сумарному магнітному заряду в заданій області простору. В зв’язку з тим, що магнітні заряди завжди існують як диполі, сумарний заряд дорівнює 0, й відповідно маємо, що інтеграл також дорівнює 0:

– в інтегральній формі, (3.44)

– в диференціальній формі. (3.45)

Нагадаємо, що з векторного аналізу відомо: якщо дивергенція будь-якого вектора дорівнює нулю, наприклад, , то можна стверджувати, щоіснує деякий вектор ,ротор якого дорівнює вихідному вектору , тобто. Це положення ілюструє рис. 3.6.

Рисунок 3.6. До пояснення положення: якщо то існує вектор, ротор якого дорівнює ,

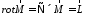
На основі цього твердження отримаємо ще одне рівняння:

, (3.46)

девекторний магнітний потенціал.

Визначимо одиницю вимірювання векторного потенціалу з (3.46).

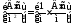, тобто .

З формули (3.46) з урахуванням (3.42) отримаємо:

. (3.47)

Виконаємо операцію ротор з лівою та правою частинами рівняння (3.47), отримаємо:

. (3.48)

На підставі (3.41) маємо:

. (3.49)

Нагадаємо положення з векторного аналізу: ротор ротора довільного вектора дорівнює:

.

Тоді з урахуванням (3.49) маємо:

. (3.50)

Оскільки векторвизначають через(3.46) та, значення якого не дорівнює нулю, тобто вектор, має вихровий характер. В той же час відомо, що дивергенція вихору дорівнює нулю, тоді в (3.50): .

Тому можемо записати:

. (3.51)

Надамо векторне співвідношення (3.51) як систему скалярних формул, як проекцій на координатні осі:

(3.52)

Ці рівняння аналогічні за формою рівнянню Пуассона (2.59). Їх розв’язок за формою також аналогічний (2.60):

(3.53)

де r – це відстань від джерела поля (яке створює струм) до точки спостереження.

Якщо помножити проекції на відповідні орти, отримаємо формулу у векторній формі:

(3.54)

У компактній формі:

. (3.54а)

Якщо визначити , то формулу (3.54а) можна записати інакше:

. (3.54б)

На основі рівняння (3.47) із урахуванням (3.54б) отримаємо:

. (3.55)

Після скорочення та заміни порядку операцій маємо :

. (3.56)

Рівняння (3.56) – це розв’язок прямої задачі магнітного поля постійного струму загальної форми: визначено напруженість магнітного поля через густину струму в просторі.

Всі одержані співвідношення застосовують для аналізу магнітних полів постійного струму в конкретних середовищах із визначеною магнітною проникністю µ. Проте, на межі двох середовищ отримані розв’язки не дають однозначну відповідь, тому потрібно з’ясувати граничні умови.