3.2. Закон повного струму

3.2.1. Закон повного струму в інтегральній формі

Визначимо роботу поля з переміщення пробного заряду вздовж замкненого контуру:

. (3.17)

Контур (рис. 3.4) може охоплювати провідники зі струмом , а може не охоплювати. Вважаємо, що струмпротікає в нескінченно тонкому і довгому провіднику. Векторє дотичною до контуру, вектор – спрямовано в тому ж напрямі, що й вектор , аперпендикулярний до нього. Напрям силових ліній вектора напруженості магнітного полявизначають за «правилом свердлика».

Рисунок 3.4. Провідник із струмом: а – охоплений контуром ; б – неохоплений контуром

Проаналізуємо першу ситуацію, коли контур охоплює струм (рис. 3.4а). Позначимо відстань від провідника до елемента контуру dl через та визначимо:

, (3.18)

.(3.19)

З правої частини (3.19) маємо: оскільки вектори і взаємно перпендикулярні, їх скалярний добуток дорівнює нулю; напрями векторівіспівпадають– добуток цих векторів дорівнює добутку їх модулів. Отже:

(3.20)

Із урахуванням, що

,(3.21)

та за умови малого кута dφ

. (3.21а)

рівняння (3.19) набуває вигляду:

. (3.22)

Із урахуванням (3.16) маємо

.(3.23)

З’ясуємо іншу ситуацію, якщо контур не охоплює провідник зі струмом. Проведемо дві прямі, дотичні до контуру в точках 1 та 2. Тоді контур умовно розділено на дві траєкторії 1а2 та 2b1:

В цій ситуації циркуляція вектора , є сума двох інтегралів:

. (3.24)

Перший інтеграл характеризує роботу поля з переміщення пробного заряду за траєкторією 1а2, а другий – за траєкторією 2b1. Оскільки кути за колами 1а2 та 2b1 однакові за значенням та протилежні за знаком в результаті маємо нуль.

Узагальнення результатів ситуацій 1 та 2 (за рис. 3.4а та рис. 3.4б) показує, що циркуляція вектора по замкненому контуру дорівнює алгебраїчній сумі струмів, які охоплює цей контур.

Таким чином, закон повного струму в інтегральній формі дає можливість розв’язку прямої задачі магнітного поля.

Для розв’язку зворотної задачі – за даними поля визначити розподіл струмів у провіднику, які створюють це поле – закон повного струму в інтегральній формі відповіді не надає. З’ясуємо закон повного стуму в диференціальній формі.

3.2.2. Закон повного струму в диференціальній формі

Визначимо в просторі точку , де напруженість поля:

(3.25)

Рисунок 3.5. До визначення закону повного струму в диференціальній формі (модель площини, яка паралельна );

Визначимо циркуляцію вектора навколо точки, спочатку в площині (рис. 3.5).

(3.26)

Відповідно до рис. 3.5 із урахуванням напряму руху за контуром 12341 формула (3.26) є такою:

. (3.26а)

Визначимо з урахуванням зміненнявздовж осіх

. (3.27)

Тоді

. (3.28)

Те ж саме запишемо для інших сторін чотирикутника:

, (3.28а)

, (3.28б)

. (3.28в)

Об’єднаємо (3.28) … (3.28в):

. (3.29)

Це закон повного струму за контуром 12341 – в дужках маємо проекцію густини струму (за напрямком ). Аналогічно для площинта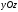отримаємо:

: , (3.30)

в дужках густина струму (за напрямком );

:, (3.31)

в дужках густина струму J_x (за напрямком ).

Тобто співвідношення для густини струму в різних напрямках:

; (3.32)

; (3.32а)

. (3.32б)

Границі від правих частин рівнянь, (3.32)…(3.32б) є проекції ротора на осі, перпендикулярні відповідним площинам:

, (3.33)

, (3.33а)

. (3.33б)

Узагальнено:

. (3.34)

Таким чином межа відношення циркуляції вектора до елемента площини за умов прямування цієї площини до нуля є проекція ротора цього вектора на нормаль до даної площини.

Тобто можемо трактувати операцію rot, як диференціальну характеристику циркуляції.

В декартовій системі координат ротор визначають:

. (3.36)

Тобто закон повного струму в диференціальній формі є

. (3.37)

У компактній матричній формі операцію визначають як

=. (3.38)