
- •3. Магнітне поле постійного струму
- •3.1. Основні характеристики магнітного поля постійного струму.
- •3.2. Закон повного струму
- •3.2.1. Закон повного струму в інтегральній формі
- •3.2.2. Закон повного струму в диференціальній формі
- •3.2.3. Перетворення (теорема) Стокса
- •3.3. Розв’язування прямої задачі магнітного поля постійного струму у загальній формі
- •3.4. Граничні умови магнітного поля постійного струму
- •3.4.1. Нормальні складники векторів та
- •3.4.2. Тангенціальні складники векторів та
- •3.4.3. Граничні умови на поверхні ідеального провідника
- •3.5. Поняття індуктивності. Енергія магнітного поля постійного
- •3.6. Висновки
- •3.7. Контрольні питання та завдання
3. Магнітне поле постійного струму
3.1. Основні характеристики магнітного поля постійного струму. Закон Біо-Савара
3.2. Закон повного струму
3.2.1. Закон повного струму в інтегральній формі
3.2.2. Закон повного струму в диференціальній формі
3.2.3. Перетворення (теорема) Стокса
3.3. Розв’язування прямої задачі магнітного поля постійного струму у загальній формі
3.4. Граничні умови магнітного поля постійного струму
3.4.1. Нормальні складники
векторів
 та
та
3.4.2. Тангенціальні складники
векторів
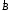 та
та
3.4.3. Граничні умови на поверхні ідеального провідника
3.5. Поняття індуктивності. Енергія магнітного поля постійного струму
3.6. Висновки
3.7. Контрольні питання та завдання
В процесі роботи з матеріалом цього розділу та після його завершення, ви маєте знати:
– модель магнітної спиці та аналог закону взаємодії електричних і магнітних зарядів
– основні характеристики магнітного поля постійного струму та зв’язок між ними;
– сутність понять «магнітна сприйнятливість», «магнітна проникність» та «намагніченість»;
– закон Біо-Савара;
– закон повного струму в інтегральній формі
– закон повного струму в диференціальній формі;
– математичне та фізичне визначення циркуляції та ротора;
– перетворення (теорема) Стокса;
– сутність векторного магнітного потенціалу;
– формування та розвиток аналогу рівняння Пуассона для магнітного поля постійного струму;
– граничні
умови магнітного поля постійного струму
для нормальних і тангенціальних
складників векторів та
та ;
;
– особливість граничних умов на поверхні ідеального провідника;
– визначення поняття індуктивності;
– визначення енергії поля постійного струму;
вміти:
– визначати силу взаємодії магнітних зарядів;
– визначати напруженість магнітного поля;
– розраховувати значення вектора магнітної індукції;
– застосовувати закон повного струму в диференціальній формі;
– застосовувати закон повного струму в інтегральній формі;
– довести та застосовувати теорему (перетворення) Стокса;
– розв’язувати пряму та обернену задачу магнітостатики в загальній формі;
– визначати
циркуляцію вектора
 ;
;
– визначати векторний магнітний потенціал;
– отримати
нормальний та тангенціальний складники
векторів
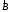 та
та ;
;
– визначати граничні умови на поверхні ідеального провідника;
– розраховувати індуктивність, як фізичну величину для соленоїда (дроселя);
– розраховувати енергію магнітного поля постійного струму.
3.1. Основні характеристики магнітного поля постійного струму.
Закон Біо-Савара
Сили, які можна виявити за умови взаємодії струмів та дії магнітів, мають однакову природу – їх називають магнітними. Джерелом магнітних сил є магнітне поле, яке існує в просторі, що оточує магніти та провідники зі струмом. Будь-який рухомий електричний заряд створює в навколишньому середовищі магнітне поле. Воно неперервне у просторі та впливає на інші рухомі електричні заряди. Скрізь, де є електричний струм, тобто рухомі електричні заряди, існує магнітне поле. Електричний струм та магнітне поле пов’язані між собою. Через те, що магнітне поле виникає навколо провідника, коли в ньому є струм, його вважають джерелом магнітного поля. Саме так треба розуміти висловлювання «магнітне поле струму», «магнітне поле, створене струмом».
Одним із способів виявлення магнітного поля навколо провідника є використання залізних ошурків. У магнітному полі ці шматочки заліза намагнічуються, та зміщуються так, що їх вісь збігається з напрямком магнітного поля у даній точці. Під час проходження постійного струму крізь провідник пропущений, наприклад, через лист картону з залізними ошурками, вони розміщуються навколо нього за концентричними колами.
За аналогією з електростатикою введемо поняття «магнітних зарядів». На відміну від електричних зарядів, окремих магнітних зарядів одного знаку в природі не існує, тому скільки б не розрізали навпіл магніт, він завжди матиме два полюси (рис. 3.1а). Тому для спрощення досліджень застосовують модель магніту у вигляді довгої, нескінченно тонкої магнітної «спиці» (рис.3.1б), внаслідок чого фіктивні магнітні заряди протилежних знаків «зосереджуються» на її кінцях.

Рисунок 3.1. Модель: а – магніту; б – магнітної спиці
Для такої моделі магніту можна за аналогією скористатись законами та положеннями електростатики. Аналогія закону Кулона для магнітної спиці:
 , (3.1)
, (3.1)
 ,
,
 – фіктивні магнітні заряди,
– фіктивні магнітні заряди, – відстань між ними,
– відстань між ними, –
магнітна проникність середовища. Вектор
напруженості електричного поля визначають
як (2.4):
–
магнітна проникність середовища. Вектор
напруженості електричного поля визначають
як (2.4):

 ,
,
за аналогією запишемо вектор напруженості магнітного поля:
 . (3.2)
. (3.2)
Одиниця вимірювання
 .
.
Визначимо одиниці вимірювання
 за формулою (3.2):
за формулою (3.2): ,
звідки
,
звідки
В електростатиці вектор
електричного зміщення (в літературі
попередніх років його називали «вектор
електричної
індукції»)
 характеризує електричне поле незалежно
від середовища, в якому це поле існує.
За аналогією з електростатикою введемо
поняття «вектор магнітної
індукції»:
характеризує електричне поле незалежно
від середовища, в якому це поле існує.
За аналогією з електростатикою введемо
поняття «вектор магнітної
індукції»:
 . (3.3)
. (3.3)
За фізичною сутністю вектор
 – цегустина магнітного
потоку.
– цегустина магнітного
потоку.
Визначимо одиницю вимірювання вектора магнітної індукції.
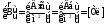 ,
,
 .
.
Деякі об’єкти, які розташовано в магнітному полі, мають здатність до намагнічування. Це явище характеризую вектор намагніченості
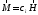 , (3.4)
, (3.4)
де М –
намагніченість речовини,
 – магнітна відносна сприйнятливість.
– магнітна відносна сприйнятливість.
За Національним стандартом України ДСТУ 2843 намагніченість – це векторна величина, якою характеризують магнітний стан речовини, яку визначають як границю відношення магнітного моменту елементів об‘єму речовини до цього елемента об‘єму, коли останній прямує до нуля.
За Національним стандартом України ДСТУ 2843 магнітна сприйнятливість – це величина, яка характеризує властивість речовини намагнічуватись у магнітному полі і яку визначають, як відношення модуля намагніченості до модуля напруженості магнітного поля, вона скалярна для ізотропної речовини.
Для магнітних речовин вектор магнітної індукції визначають:
 .
(3.5)
.
(3.5)
де µ – абсолютна магнітна проникність,
 –відносна магнітна
сприйнятливість,
–відносна магнітна
сприйнятливість,
 –відносна магнітна проникність,
–відносна магнітна проникність,
 –магнітна проникність у
вакуумі (магнітна стала).
–магнітна проникність у
вакуумі (магнітна стала).
Магнітна проникність
 – величина, що показує, наскільки
індукція
– величина, що показує, наскільки
індукція магнітного поля в однорідному середовищі
відрізняється від індукції
магнітного поля в однорідному середовищі
відрізняється від індукції магнітного поля в вакуумі. Для
діамагнетиків, тобто речовин, що
послаблюють магнітну індукцію зовнішнього
поля,
магнітного поля в вакуумі. Для
діамагнетиків, тобто речовин, що
послаблюють магнітну індукцію зовнішнього
поля,
 .
Для парамагнетиків , що підсилюють
магнітну індукцію зовнішнього поля
.
Для парамагнетиків , що підсилюють
магнітну індукцію зовнішнього поля
 .
Для феромагнетиків, що мають власну
намагніченість і внутрішнє магнітне
поле у багато разів перевищує зовнішнє
поле,
.
Для феромагнетиків, що мають власну
намагніченість і внутрішнє магнітне
поле у багато разів перевищує зовнішнє
поле,
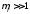 .
.
Для монохромного поля та
неоднорідного лінійного ізотропного
середовища магнітна проникність у
загальному випадку є функцією узагальнених
криволінійних координат.
Тоді маємо:
 . (3.6)
. (3.6)
Якщо середовище нелінійне, тобто μ=μ(Н), маємо:
 .
(3.6а)
.
(3.6а)
Для монохромного поля, однорідного лінійного анізотропного середовища:
 (3.7)
(3.7)
де сукупність чисел
 має назвутензор:
має назвутензор:

У спрощеній формі:
 (3.8)
(3.8)
З’ясуємо визначення магнітного поля, яке створює постійний електричний струм. В основі розв‘язання прямої задачі магнітного поля постійного струму покладено закон Біо – Савара, відкритий експериментально у 1820 р.:
 ,
(3.9)
,
(3.9)
де
 називають «елементом струму», що є
вектором за яким визначають модуль та
напрямок елементу
називають «елементом струму», що є
вектором за яким визначають модуль та
напрямок елементу .
.
Закон Біо-Савара
свідчить про те, що
напруженість магнітного поля,
яку створює елемент постійного струму
 ,прямо пропорційна
значенню цієї величини,
обернено пропорційна
квадрату відстані до точки спостереження
та залежить від напрямку
на неї (рис. 3.2).
,прямо пропорційна
значенню цієї величини,
обернено пропорційна
квадрату відстані до точки спостереження
та залежить від напрямку
на неї (рис. 3.2).

Рисунок
3.2. До визначення напрямку вектора
 :а
–
на площині; б
–
умовно в просторі
:а
–
на площині; б
–
умовно в просторі
Визначимо модуль
 :
:
 , (3.10)
, (3.10)
де
 ,
, – кут між напрямком
– кут між напрямком та одиничним вектором
та одиничним вектором .
.
Загальне поле за принципом суперпозиції визначають за результатом інтегрування за всіма елементами струму.
Тоді рівняння для напруженості магнітного поля набуде вигляду:
 . (3.11)
. (3.11)
З’ясуємо приклад застосування
закону Біо-Савара для нескінченно
довгого тонкого провідника
 зі струмом
зі струмом
 .
На відстані
.
На відстані
 від провідника є точка спостереженняD, через
яку проходять силові лінії магнітного
поля (рис 3.3).
від провідника є точка спостереженняD, через
яку проходять силові лінії магнітного
поля (рис 3.3).

Рисунок 3.3. До визначення напруженості магнітного поля
Інтеграл (3.11) має нескінченні межі інтегрування. Для того, щоб конкретизувати межі інтегрування, використаємо співвідношення із трикутників АВС, ВСD відповідно:
 , (3.12)
, (3.12)
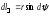 ≈
≈ . (3.13)
. (3.13)
Після заміни
 (3.11) на rd
(3.13) із урахуванням (3.12) та заміни меж
інтегрування, маємо
(3.11) на rd
(3.13) із урахуванням (3.12) та заміни меж
інтегрування, маємо
 . (3.14)
. (3.14)
З трикутника АЕD
(із врахуванням, що внаслідок нескінченно
малого значення
 AD=BD)
маємо:
AD=BD)
маємо:
 .
.
Підставимо цю формулу в рівняння (3.14) та отримаємо:
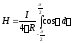 .
(3.15)
.
(3.15)
Після інтегрування (3.15), для напруженості магнітного поля маємо:
 , (3.16)
, (3.16)
Визначимо ,
як вектор:
,
як вектор:
 ,
(3.16а)
,
(3.16а)
де
 –
це вектор перпендикулярний до площини
з провідником із струмом та вектором
–
це вектор перпендикулярний до площини
з провідником із струмом та вектором
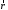 .
.
Таким чином встановлено, що
значення напруженості магнітного поля,
яку створює нескінченно довгий провідник
зі струмом
 ,
визначають за формулою (3.16), напрямок
вектора
,
визначають за формулою (3.16), напрямок
вектора визначають за дотичною до концентричних
кіл навколо провідника зі струмом.
визначають за дотичною до концентричних
кіл навколо провідника зі струмом.
Застосування закону Біо-Савара для аналізу провідника фіксованої довжини з визначеним діаметром вимагає складного інтегрування, тому потрібен інший підхід до розрахунку магнітного поля.
Такий підхід ґрунтується на законі повного струму (круговий закон Ампера).
