9.2.2. Вектор зорієнтовано паралельно площині падіння

Ілюстрацію процесу похилого падіння електромагнітної хвилі типу T за орієнтацією вектора паралельно площині падіння наведено на рис. 9.9.

Рисунок 9.9. Складники поля за умови, якщо вектор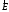паралельний площині падіння

Нагадаємо – площина падіння є площиною з вектором Пойнтинга та нормаллю до межі середовищ. В цій ситуації вектори тахвилі, що падає, мають такі складники:

, (9.25)

. (9.26)

Щоб записати синтезовані складники, необхідно здійснити ті ж операції, що і в попередньому пункті.

Уздовж осі поширюєтьсярухома хвиля, а уздовж осі – сформовананерухома хвиля.

В цьому випадку вектор на підставі граничних умов () на межі поділу має не нульове значення, його напрям після відбиття не змінюється (рис. 9.9). Тому у формулі дляза віссюповинна бути функція, адже; за часом функція може бути будь-яка, наприклад також:

. (9.27)

Складники електричного поля разом зформують рухому хвилю уздовж осі, вони є у «фазі» (), тобто знову використовуємо функцію:

, (9.28)

де .

Складник електричного поля разом з векторомутворюють уздовж осінерухому хвилю – вони є в квадратурі. Для забезпечення відповідного позитивного напряму вздовж осіу формуліпередує знак мінус:

, (9.29)

де .

Далі за визначеними вище правилами формуємо структуру поля: уздовж осі z (рис 9.10а), – осі x (рис 9.10б) та загальну – (рис 9.10в). Для зазначених складників ,,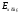знаки вздовж осейприйнято +. Додатково перевіряємо, щоб лінії поля вектора«спирались» на межу розподілу (рис 9.10в).

Рисунок 9.10. Структура поля за умови, що 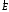паралельний площині падіння:а– вздовж осі;б– вздовж осі;в– результуюча

Формулюємо висновок: оскільки в результаті силові лінії напруженості магнітного поля мають складники тато з хвилітипу , сформовано поздовжню хвилю типу , або поперечну електричну хвилю – типу_, якщо вектор паралельний площини падіння.

9.3. Висновки

1. Електромагнітні хвилі можна розділити на дві групи. До першої групи належать ті, що мають лише поперечні складники – це пари–та–, апоздовжні відсутні. Така хвиля має назву хвиля типу Т або поперечна електромагнітна (ТЕМ).

2. Однак, у просторі можуть існувати також хвилі іншої групи, тобто хвилі, у складі яких є складники та: якщо, або. Ціпоздовжні хвилі, відповідно, мають назву хвилі типу , абопоперечні електричні (ТЕ) та хвилі типу , абопоперечні магнітні (ТМ).

3. За умов падіння електромагнітної хвилі типу Т на ідеально-провідну поверхню утворюється відбита хвиля й поле спрямовано вздовж ідеально-провідної поверхні.

4. Отриманий вектор має два складника:

– уздовж осі (характеризує режим нерухомої хвилі);

– уздовж осі (характеризує режим рухомої хвилі).

5. У напівобмеженому просторі електромагнітна хвиля характеризується трьома швидкостями: фронту , фазита груповій(зауважимо, що ). . У вільному просторі.

6. За умов падіння електромагнітної хвилі на ідеально-провідну поверхню доцільно ввести поняття характеристичного опору , який визначають через хвильовий імпеданста кут падіння.

7. Структури полів електричних та магнітних векторів різні за умов різної орієнтації вектора хвилі що падає типуТ:

– якщо вектор зорієнтованоперпендикулярно площині падіння – в результаті сформовано хвиля типу Н (ТЕ);

– якщо вектор зорієнтованопаралельно площині падіння – в результаті сформовано хвиля типу Е (ТН).

8. Конструкція, складена із майже ідеальних провідних стінок, є основою хвилеводів.