9.2. Структура електромагнітного поля над ідеально- провідною поверхнею

Поняття «структура поля» визначає сукупність у просторі векторів тасформованої хвилі. Необхідно з’ясувати структуру поля електромагнітної хвилі для двох ситуацій:

– вектор хвилі, що падає, перпендикулярний площині падіння;

– вектор хвилі, що падає, паралельний площині падіння.

9.2.1. Вектор зорієнтовано перпендикулярно площині падіння

Ілюстрацію процесу похилого падіння електромагнітної хвилі типу T за орієнтацією вектора перпендикулярно площині падіння наведено на рис. 9.6.

Рисунок 9.6. Складники поля за умови, якщо вектор перпендикулярний площині падіння

Взаємна орієнтація векторів хвилі, що падає є:

, (9.9)

. (9.10)

На підставі граничних умов, з урахуванням того, що на поверхні ідеального провідника маємо:

, (9.11)

. (9.11а)

Знак «мінус» в (9.11а) означає, що напрям відбитого вектора змінюється на протилежний.

Відповідно до напряму вектора Пойнтинга запишемо.

. (9.12)

Отримане в результаті значення , визначимо, додаванням миттєвих значень відповідних проекцій хвилі, що падає та відбитої хвилі. Нехай у точцімаємо:

, (9.13)

. (9.13а)

Тоді, в точках тавідповідно:

, (9.14)

. (9.15)

Напруженість у довільній точці визначимо додаванням (9.14) та (9.15). Нагадаємо:. Тоді:

. (9.16)

Із урахуванням, що , маємо:

. (9.16а)

Звернемось до співмножника, що не залежить від часу – він визначає амплітуду:

. (9.17)

Таким чином, амплітуда поля залежить від координати . На осііснують точки, де, що мають назвувузли, та пучності – , тобто вздовж осісформована нерухома хвиля (рис. 9.7).

Рисунок 9.7. Ілюстрація напруженості поля у формі нерухомої хвилі

Вузли напруженості поля є за умов , де , тобто

. (9.18)

Довжина нерухомої хвилі – див. формулу 9.3.

Для визначення складників вектора 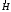можна двома способами:

– виконати усі операції, як із вектором ;

– використати співвідношення між тачерез хвильовий імпеданс.

Скористаємось останнім; з урахованням, що середовище – вільний простір, для якого хвильовий імпеданс – активний : .

Визначимо співвідношення між складниками та.

, (9.19)

де ,так званий, характеристичний опір. За аналогією для відбитої хвилі:

. (9.19а)

З (9.19) та (9.19а), якщо вважати, що – дійсна додатна величина (за умов вільного простору), випливає, що поперечні складники електричного та магнітного полів хвилі, що падає, та відбитої, однакові, тобто змінюються за тим самим законом.

Тоді:

. (9.20)

Визначимо на підставі граничних умов для тангенціальних складників векторана межі розподілу з ідеальним провідником. Як видно з рис. 9.6 тангенціальний складник після відбиття не змінюється, тобто:

,

. (9.21)

У співвідношеннях між тадля будь-якої точки поля вздовж осідля конкретного значення координати маємо додатковий зсув за фазою.

Запишемо співвідношення (9.16а), (9.20), (9.21) з урахуванням додаткового зсуву за фазою таким чином:

; (9.22)

; (9.23)

. (9.24)

Формуємо структуру поля в момент . Для цього виконуємо таке:

1) приймаємо за основу формули складових поля уздовж осей та(9.22...9.24);

2) умовно визначаємо знаки співмножників уздовж осей таз урахуванням знаків в формулах (9.22...9.24) аргументу:

3) починаємо укладення структури поля з осі :(рис. 9.8а);

4) наводимо вздовж осі(рис. 9.8б);

5) перемножуємо складники:;;та наводимо зорієнтовані криві на рис. 9.8в;

6) перша перевірка – лінії вектора замкнені, друга перевірка – лінії вектора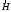спрямовані вздовж межі – є дотичними;

7) наводимо вектори так само: вони є в площині, що перпендикулярна площині аркуша (рис. 9.8в).

Формулюємо висновок: оскільки в результаті силові лінії напруженості магнітного поля мають складники тато з хвилітипу , сформовано поздовжню хвилю типу , або поперечну електричну хвилю – типу_, якщо вектор перпендикулярний площини падіння.

Рисунок 9.8. Структура поля за умови, що перпендикулярний площині падіння:

а– складники вздовж осі;б– складники вздовж осі;в– результивне