
П.Г.Фрик - Турбулентность модели и подходы, часть 1
.pdf
21
1.2 Устойчивостьтечений
Вопрос об устойчивости того или иного состояния (реш ения, режима) возникает в самых разных задачах. Достаточно вспомнить простейш ий пример об устойчивости ш арика, лежащ его на различных поверхностях (рис.1.7). В первом случае положение ш арика абсолютно устойчиво, то есть при любом конечном воздействии ш арик по окончании действия возму-
ùаю щ ей силы возвращ ается в исходноесостояние. Во втором случае положение ш арика абсолю тно неустойчиво - любое, сколь угодно малое возму-
ùение, безвозвратно уводит его из начального положения. Третий случай иллю стрирует пример состояния, устойчивого по отнош ению к малым возмущ ениям, но наруш аю щ е- гося, если возмущ ения превышаю т критическую вели- чину.
Íас интересует вопрос
об устойчивости стационарных течений. Для конкретности будем говорить о те- чении П уазейля. Возмущ е-
ния в реальных течениях сущ ествую т всегда. И х источником служат ш ероховатости стенок, входные участки (бесконечных труб нет), просто флуктуации характеристик самой жидкости и т.д. Н ужно ответить на вопрос о том, какое возмущ ение является самым опасным и где та граница, при превышении которой это возмущ ение приведет к разруш ению сущ ествую щ его течения.
И так, имеем течение несжимаемой жидкости, для которой запиш ем уравнения Н авье-Стокса в безразмерной форме(1.14)
¶v |
|
r r |
|
1 |
r |
|
|
+ |
(vÑ )v |
= - Ñ P + |
|
Dv, |
|
¶t |
R |
|||||
r |
= 0. |
|
|
|||
div v |
|
|
|
|||
Стационарное реш ение задачи (имеем в виду течениеП уазейля, хотя до определенного этапа все рассуждения не зависят от конкретного вида реш ения) обозначим как v0 , P0 . Это реш ение, в свою очередь, удовлетворя-
етуравнениям
r |
|
r |
|
|
1 |
r |
|
|
|
(v0 |
Ñ )v0 |
= - Ñ P0 |
+ |
|
Dv0 |
, |
(1.15) |
||
R |
|||||||||
|
r |
= 0. |
|
|
|
||||
|
|
|
|
|
|
||||
div v0 |
|
|
|
|
|
||||
22
Ïоляскорости и давления представим в видесумм стационарных ре-
øений и возмущ ений
v(x, y, z, t) = v0 (z) + v (x, y, z, t), |
(1.16) |
||
P(x, y, z, t) = P0 (z) + |
P¢(x, y, z, t). |
||
|
|||
Отметим, что в отличие от исследуемого стационарного реш ения, слагаемые со ш трихами описываю т возмущ ения, которые могут зависеть от времени и от всех координат. Введенные разложения подставляю тся в исходные уравнения
¶v |
|
r r |
|
r r r r |
|
r r |
|
1 |
r |
|
1 |
r |
|
|||
|
+ |
(v0 Ñ )v0 |
+ |
(v0 |
Ñ )v ¢+ |
(v ¢Ñ )v0 |
+ |
(v ¢Ñ )v ¢ = - Ñ P0 |
- Ñ P¢+ |
|
Dv0 |
+ |
|
Dv ¢ |
(1.17) |
|
¶t |
R |
R |
||||||||||||||
r |
r |
|
|
|
|
|
|
|
|
|
|
|||||
div v0 |
+ div v ¢= 0 |
|
|
|
|
|
|
|
|
|
|
|
||||
и, после вычитания из них уравнений для стационарных реш ений (1.15), получаем
¶v |
|
r |
r |
r r |
|
r r |
1 |
r |
|
|
|
+ |
(v0 |
Ñ )v ¢+ |
(v ¢Ñ )v0 |
+ |
(v ¢Ñ )v ¢ = - Ñ P¢+ |
|
Dv ¢, |
(1.18) |
|
¶t |
R |
|||||||||
r |
|
|
|
|
|
|||||
div v |
¢= 0. |
|
|
|
|
|
|
|||
Н аибольш ие трудности в реш ении этих уравнений представляет нелинейное по искомым возмущ ениям слагаемое (v Ñ )v . Следую щ ий, принципиальный ш аг состоит в том, что это слагаемое отбрасывается. Тем самым мы ограничиваем себя рамками линейной теории устойчивости, рассматриваю щ ей эволю цию малыхвозмущ ений. Это значит, что
| v | << | v0 | .
Линейная теория работает только вблизи порога возникновения неустойчивости. П о прохождению порога, возмущ ения нарастаю т и линейные уравнения перестаю т работать. Тем неменее, поставленная задача при этом может считаться выполненной, так как требовалось указать именно сам порог и наиболееопасныевозмущ ения, которые начинаю т нарастать в первую очередь.
Отказавш ись от написания ш трихов, мы придем к системеуравнений, которую необходимо дополнить граничными условиями для возмущ ений. Н апример, можно предположить, что на границах возмущ ения равны нулю .
23
¶v |
|
r |
r |
|
r r |
|
1 |
r |
||
|
|
+ |
(v0 |
Ñ )v |
+ |
(vÑ )v0 |
= - Ñ P + |
|
Dv, |
|
¶t |
R |
|||||||||
r |
= 0, |
|
|
|
(1.19) |
|||||
div v |
|
|
|
|
||||||
r |
|
|
= 0. |
|
|
|
|
|
||
v |
|
à |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
Далее делаю т ещ е ряд сущ ественных упрощ ений. П ервое состоит в том, что рассматриваютсятолько плоские возмущ ения. Этот ш аг оправдывается теоремой Скваера, которая утверждает, что самыми опасными являю тсяименно плоские возмущ ения. Такое предположение означает, что
r |
|
|
|
¶ |
|
|
|
|
|
|
|
v = (vx |
,0,vz ) è |
|
= 0 . |
|
|
|
|
|
|
||
¶y |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
С учетом того, что |
|
|
|
|
|
|
|||||
r |
¶ |
|
|
|
r |
¶ |
|
¶ |
|
||
(v0Ñ )= v0 |
|
|
|
è |
(vÑ )= vx |
|
+ |
vz |
|
, |
|
¶x |
|
¶x |
¶z |
||||||||
уравнения движения для оставш ихсядвух компонент запиш утся в ви-
äå
|
¶vx |
|
+ v |
|
¶v x |
|
+ v |
|
|
¶v0 |
= - |
¶P |
+ |
1 |
Dv |
|
, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
¶t |
|
0 ¶x |
z ¶z |
¶x R |
x |
|
|||||||||||||||||||
|
|
¶vz |
+ v |
|
|
¶vz |
= - |
¶P |
+ |
1 |
Dv |
|
, |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
¶t |
|
0 |
|
|
¶x |
|
¶z R |
|
z |
|
|
|
|
|
|
||||||||||
¶vx |
+ |
¶vz |
|
= 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
¶z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Следую щ ий ш агсостоит в том, что вводится функция тока ψ , связанная с
компонентами вектора скорости: vx |
= - |
¶ψ |
vz |
= |
¶ψ |
. Введениефункции тока |
¶z |
|
|||||
|
|
|
|
¶x |
||
позволяет уменьш ить число переменных. П латой за это является повышение порядка дифференциальных уравнений, которые принимаю т вид:
− ∂ ∂ψ ∂t ∂z ∂ ∂ψ
∂t ∂x
−v0
+v0
∂2ψ
∂x∂z ∂2ψ
∂x 2
+ ∂ψ ∂v0 = − ∂P − 1 ∂ψ ,
|
∂x ∂z |
|
|
∂x |
R ∂z |
|||
= − |
|
∂P |
+ |
1 |
|
∂ψ |
|
, |
|
|
R |
|
∂x |
||||
|
|
∂z |
|
|
||||
−∂2ψ + ∂2ψ ≡ 0. ∂x∂z ∂z∂x
Ïоследнее уравнение (это уравнение непрерывности) выполняется тождественно. Это не удивительно, так как функция тока вводится именно для
24
несжимаемой жидкости. Следую щ ий ш аг также является общ епринятым - для того, чтобы избавиться от давления и получить одно уравнение для функции тока, необходимо второе уравнение продифференцировать по координате x и вычесть изнего первое, продифференцированное по координате z . Результирую щ ееуравнение есть
¶ |
æ¶2ψ |
|
|
¶2ψ |
ö |
|
|
¶ ¶2ψ |
|
|
¶2ψ |
|
¶v |
0 |
|
¶2ψ |
|
¶v |
0 |
|
¶ψ |
|
¶2 v |
0 |
|
¶2ψ |
|
¶v |
0 |
|
|
¶ ¶2ψ |
|
||||||||||||||||||||
|
ç |
|
|
|
|
|
|
+ |
|
|
|
|
÷ |
+ v |
0 |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
- |
|
|
|
- |
|
|
|
|
+ |
|
|
|
+ v |
0 |
|
|
|
|
= |
|||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
||||||||||||||||
¶t |
ç |
¶z |
|
|
¶x |
÷ |
|
¶x ¶z |
|
|
|
¶x¶z ¶z |
¶x¶z ¶z |
¶x ¶z |
|
¶x¶z ¶x |
¶x ¶x |
|
|||||||||||||||||||||||||||||||||||
è |
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
¶2 P |
|
|
|
|
¶2 P |
|
|
1 |
|
æ¶2ψ |
|
|
|
¶2ψ |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
+ |
|
|
|
|
|
+ |
|
|
|
|
Dç |
|
|
|
|
+ |
|
|
|
|
|
÷. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
¶x¶z ¶x¶z R |
ç |
¶x |
|
|
|
|
¶z |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
è |
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Сокращ ая подобные члены и учитывая, что ¶v0  ¶x = 0 , приходим к уравнению
¶x = 0 , приходим к уравнению
¶ |
Dψ + v |
|
¶ |
Dψ - v |
|
² ¶ψ |
= |
1 |
DDψ |
, |
(1.20) |
|
¶t |
0 |
¶x |
0 |
|
¶x |
R |
||||||
|
|
|
|
|
|
|
||||||
которое дополняетсяграничными условиями для функции тока:
ïðè z = ±1: ¶ψ = ¶ψ = 0
¶x ¶z
Н апомним, что функция тока введена для возмущ ений поля скорости, возникаю щ их на фонестационарного течения v0 . Ш трихами обозначено диф-
ференцирование по вертикальной координате z .
П олученное уравнение (1.20) можно реш ать численно, задавая различные начальные возмущ ения и наблюдая за их эволю цией при различ- ных числах Рейнольдса. Этот путь не снимает, однако, вопроса о выборе вида возмущ ений. Следуя обычному для теории устойчивости способу, будем рассматривать нормальныевозмущ ения, то есть возмущ ения вида
ψ (x, z,t ) = ϕ (z)ei(ω t − kx ) . |
(1.21) |
П ри это фактически мы провели |
|
разделение переменных, вклю чив |
|
зависимость от вертикальной ко- |
|
ординаты |
z только в амплитуду |
|
возмущ ений ϕ . Зависимость от |
|
продольной координаты и време- |
|
ни принята в виде гармонических |
|
волн, распространяю щ ихся вдоль |
Ðèñ. 1.8. |
îñè x (ω - частота, k - волновое |
|

25
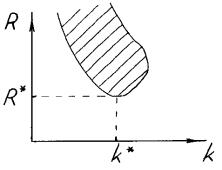
число). Частота является величиной комплексной: ω = a + ib , что позволяет переписать выражение для нормальных возмущ ений в виде
ψ (x, z,t )ϕ (z)ei(ω t − kx ) = ϕ (z)e− bt ei(at − kx ) .
Характер эволю ции колебаний во времени определяется мнимой ча- стью частоты: если b > 0 , то возмущ ения убываютсо временем, аесли b < 0 , то возмущ ения нарастаю т (см. рис.1.8). И менно знак величины b и интересен с точки зрения вопроса об устойчивости течения. Требуется узнать, при каком значении числа Рейнольдса появляетсяреш ение с отрицательным b и какоеволновое число k соответствует этому реш ению .
Возмущ ения в нормальной форме подставляются теперь в уравнение для функции тока. Соответствую щ ие производные определяю тся формулами:
¶ψ |
= iωψ , |
¶ψ |
= - ikψ , |
¶ψ |
= ϕ ¢åi(ωt − kx) , |
|
|
|
|||
¶t |
¶x |
¶z |
|||
|
|
|
|
|
|
∂2ψ |
|
∂2ψ |
|
|
2 |
|
i(ω t − kx ) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
ϕ )e |
|
|
|
|
|
|
|
|
|
|
|
|
|
Dψ = ∂x 2 + |
|
|
|
|
|
|
|
, |
|
|
|
|
|
||||||||
|
|
|
|
|
∂z 2 = (ϕ - k |
|
|
|
|
|
|
||||||||||||||
DDψ = ϕ |
IV |
- |
2 |
′ |
k |
2 |
′ |
k |
2 |
ϕ )e |
i(ω t − kx ) |
= |
(ϕ |
IV |
- |
2 |
′ |
k |
4 |
ϕ )e |
i(ω t − kx ) |
. |
|||
|
k |
ϕ - |
|
(ϕ - |
|
|
|
2k |
ϕ + |
|
|
||||||||||||||
П осле подстановки получаем
é |
′ |
|
2 |
|
|
|
′ |
2 |
|
|
² |
|
1 |
|
|
IV |
|
|
|
2 |
′ |
|
|
4 |
ù i(ω t − kx ) |
||
êiω (ϕ - |
k |
|
ϕ )- ikv0 (ϕ |
- |
k |
ϕ )+ |
ikv0 |
ϕ = |
|
|
(ϕ |
|
- |
2k |
|
ϕ |
+ |
k |
|
ϕ )úe |
|||||||
|
R |
|
|
|
|||||||||||||||||||||||
ë |
|
|
|
|
|
|
|
|
|
² |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
û |
||
|
|
|
|
|
|
′ |
2 |
|
|
|
|
|
IV |
|
|
2 |
|
|
′ |
|
4 |
|
|
|
|||
|
|
(iω - |
ikv0 )(ϕ |
|
- k |
ϕ )+ ikv0 ϕ = |
|
|
(ϕ |
|
- |
2k |
ϕ |
+ |
k |
|
ϕ ), |
||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
а после деления на ik и добавления граничных условий приходим к окон- чательной форме уравнения, называемого уравнением Орра-Зоммерфельда (1937г.):
æ |
|
|
|
ω ö |
|
|
|
2 |
² |
i IV |
2 |
|
4 |
|
||
çv |
0 - |
|
|
′ |
|
k ϕ )- v0 ϕ = |
|
(ϕ - |
|
′ |
|
ϕ ), |
||||
|
|
|
|
|
|
|||||||||||
|
÷(ϕ - |
|
kR |
2k ϕ + k |
|
|||||||||||
è |
|
|
|
k ø |
|
¢ |
|
|
|
|
|
|
(1.22) |
|||
ϕ |
|
|
|
= 0 ϕ |
|
= 0. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
z =±1 |
|
|
|
|
z =±1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задача остается чрезвычайно сложной и впервые для плоского слоя была реш ена только в 1945 г. Линем. П оучительна история реш ения этого уравнения. П ервые подходы были связаны с попытками реш ать уравнение Орра-Зоммерфельда с отброш енной правой частью . Соответствую щ ее
26
уравнение называют уравнением Релея. Отметим, что отбрасывая члены с четвертой производной ϕ IV , мы лиш аемся возможности использовать все граничные условия и можем требовать обращ ения в нуль только нормальной компоненты скорости (этому соответствует условие ∂ψ 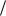 ∂x = 0 è ϕ = 0 ). Отбрасывание правой части мотивировалось тем, что она описывает действие вязкости, а вязкость, казалось, должна играть стабилизирую щ ую роль. Результат реш ения уравнения Релея состоял в том, что оно оказывалось абсолю тно устойчивым.
∂x = 0 è ϕ = 0 ). Отбрасывание правой части мотивировалось тем, что она описывает действие вязкости, а вязкость, казалось, должна играть стабилизирую щ ую роль. Результат реш ения уравнения Релея состоял в том, что оно оказывалось абсолю тно устойчивым.
Линь показал, что фазовая скорость возмущ ений vô = ω / k меньш емаксимальной скоро-
сти потока в центре слоя. Точки, в которых фазовая скорость возмущ ений совпадает со скоростью основного течения, являю тся критиче- скими и именно вблизи этих точек начинается нарастание возмущ ений. Основной результат исследования уравнения Орра-Зоммерфельда качественно иллю стрируется рисунком 1.9, на котором представлена так называемая нейтральная кривая, нарисованная на плоскости
k − R . Область неустойчивости заш трихована. Критические параметры отмечены на рисункезвездочками. Н аименьш ее значение числа Рейнольдса, при котором начинаетсярост возмущ ений R* = 5700 . Соответствую щ ееему
критическое значение волнового числа k * ≈ 1. Это означает, что наиболее опасными возмущ ениями являю тся возмущ ения с длиной волны, превы-
øаю щ ей толщ ину слоя приблизительно в 2π ðàç.
Èнтересна ещ е одна особенность нейтральной кривой. П ри некоторых значениях волнового числа в область неустойчивости можно попасть и двигаясь от больш их чисел Рейнольдса к малым. Это означает, что вязкостьможетиграть и дестабилизирую щ ую роль.
1.3Свободная конвекция несжимаемой жидкости
Ïод свободной конвекцией понимаю т движения жидкости, возникаю щ ие за счет сил Архимеда при наличии неоднородности плотности жидкости в поле массовых сил. В основном будем рассматривать термогравитационную конвекцию, т.е. случай, когда неоднородности жидкости
связаны с ее неравномерным нагревом и течение возникает в поле силы тяжести. П ри этом будем иметь в виду жидкости, плотностькоторых падаетсростом температуры, т.е. ∂ρ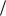 ∂T < 0 (напомним, что аномальное поведе-
∂T < 0 (напомним, что аномальное поведе-
27
ние дает вода в интервале от 0 до 4î С). Считаем, что неоднородность температуры являетсяединственным источником движения и что
Dρ << ρ ,
т.е. рассматривается слабая конвекция. В уравнении движения появляетсяслагаемое, описываю щ еедействие силы тяжести
|
é¶v |
r rù |
r |
r |
|
ρ |
ê |
|
+ (vÑ )v ú |
= - Ñ P + ηDv |
+ ρg |
|
|||||
|
ë¶t |
û |
|
|
|
и нужно учесть изменения плотности. П оследняя в общ ем случае есть функция температуры и давления ρ = ρ(T , P), а приращ ение плотности есть
æ¶ρ ö |
|
æ¶ρ ö |
||||
dρ = ç |
|
÷ |
dT + |
ç |
|
÷ dP . |
|
|
|||||
è¶T øP |
|
è¶P øT |
||||
Далееделается важное ограничение, состоящ еев том, что рассматривается несжимаемая жидкость, означаю щ ее что вторым слагаемым в этом равенстве можно пренебречь. Таким образом, полагается, что плотностьзависит только от температуры: ρ = ρ(T ), а приращ ение плотности есть
|
1 |
æ¶ρ ö |
||
dρ = |
|
ç |
|
÷ρ0 dT = - βρ0 dT . |
ρ0 |
|
|||
|
è¶T ø |
|||
Здесь |
β - коэффициент объемного расш ирения. Температуру жидко- |
||
сти представим в виде |
|
|
|
|
T = T0 + T , |
(1.23) |
|
ãäå T0 - средняя температура, а |
T - вариации температуры, малые в том |
||
смысле, что |
вызываемые ими |
вариации |
плотности остаются малыми |
( Dρ << ρ ). П лотность представляется, соответственно, в виде ρ = ρ0 + ρ (T ) , ãäå ρ0 - плотностьжидкости при температуре T0 . И зсказанного вышеследует, что
ρ = - ρ0 βT |
|
èëè |
|
ρ = ρ0 (1 - βT ). |
(1.24) |
П ринятое ограничение слабой конвекции |
предполагает, что βT << 1 . |
Вспомним, что для воды β = 2 ×10− 4 , и следовательно приближение годится

28
практически для любых возможных разностей температуры. Для газов β »1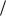 273 , что сущ ественно больш е, но также позволяет пользоваться принятыми ограничениями при достаточно больш их разностях температуры.
273 , что сущ ественно больш е, но также позволяет пользоваться принятыми ограничениями при достаточно больш их разностях температуры.
И зотермической жидкости с температурой T = T0 и соответствую щ ей этой температуре плотностью ρ = ρ0 отвечает гидростатическое давление P0 , подчиняю щ ееся уравнению
ÑP0 = ρ0 g .
Ïоле давления, устанавливаю щ ееся при конвективном движении, представим в видесуммы
P = P0 + P .
П одставляя в уравнения движения всевведенныеразложения, получаем
(ρ + ρ¢)é¶v 0 êë¶t
|
r |
|
r |
= - Ñ P |
|||
+ (vÑ )v |
ù |
||||||
|
|
|
|
ú |
|
|
0 |
|
¶ρ |
|
|
û |
|
r |
|
|
+ |
|
|
|
+ |
||
|
|
|
ρ0 |
div v |
|||
|
¶t |
|
|||||
|
|
|
|
|
|
|
|
r
- Ñ P¢+ ηDv +
r
div ρ¢v = 0 .
rr
ρ0 g + ρ¢g ,
Теперь нужно вычесть из первого уравнения уравнение гидростатики и сделать самое важное допущ ение. Оно состоит в том, что добавкой к плотности ρ , возникаю щ ей за счет изменения температуры, пренебрегаю т всю - ду, заисклю чением члена, описываю щ его силу Архимеда. Тогда
é¶v |
r rù |
|
r |
r |
||
ρ0 ê |
|
+ (vÑ )v |
ú |
= - Ñ P¢+ η |
v |
- βT ¢g . |
|
||||||
ë¶t |
|
û |
|
|
|
|
Систему необходимо дополнить уравнением для температуры. Если пренебречь нагревом жидкости за счет вязкой диссипации, то закон переноса удельной энергии записывается в виде
é¶S |
r |
ù |
|
||
ρT ê |
|
|
+ (vÑ )S ú |
= κDT , |
|
|
¶t |
||||
ë |
|
û |
|
||
ãäå κ - коэффициент теплопроводности, а энтропия S связана с температурой и давлением
S = S0 + |
æ |
¶S ö |
T ¢+ |
æ¶S ö |
P¢. |
|||
ç |
|
÷ |
ç |
|
÷ |
|||
|
|
|||||||
|
è¶T øP |
|
è¶P øT |
|
||||
И спользуясоотнош ение

29
æ |
¶S ö |
= |
ñp |
|
ç |
|
÷ |
|
|
|
T0 |
|||
è¶T øP |
|
|||
и считая третье слагаемое пренебрежимо малым (это логично сделать, так как зависимостью плотности от давления уже пренебрегли), приходим к соотнош ению
S = S0 |
+ |
c p |
¢ |
|
|||
T0 |
T . |
||
|
|
|
П одставляя в уравнение для энтропии и ограничиваясь членами, линейными по T , получаем
¶T |
r |
κ |
|
|
+ (vÑ )T ¢= |
|
DT ¢. |
¶t |
ρc p |
Далее, откажемся от написания ш трихов (незабывая при этом, что температура отсчитывается от среднего значения, а давление - от гидростатиче- ского давления) и запиш ем результат - систему уравнений для термогравитационной конвекции несжимаемой жидкости в приближении Буссинеска
|
¶v |
|
|
r |
r |
|
Ñ P |
r |
|
r |
|
|
|
|
+ |
(vÑ )v |
= - |
|
|
+ νDv |
+ |
gβTez |
, |
||
|
¶t |
ρ0 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
¶T |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
+ |
(vÑ )T = χDT , |
|
|
|
(1.25) |
||||
|
¶t |
|
|
|
|
|||||||
|
|
r |
= 0. |
|
|
|
|
|
|
|
||
div v |
|
|
|
|
|
|
|
|||||
Ì û ó÷ëè, ÷òî g = - gez |
è |
ввели |
коэффициент температуропроводности |
|||||||||
χ = κ / ρc p . Систему необходимо дополнить граничными условиями. Для скорости можно принять, например, условия прилипания ( v |Ã = 0 ), а для температуры - либо задать ее распределение на границе (T | Ã = f1 (Ã) ), либо теплопоток через границу
¶T
¶n Ã
= f2 ( Ã) .
Обсудим возможные способы представления уравнений свободной конвекции в безразмерной форме. Особенностью конвективных задач является отсутствие заданной характерной скорости - скорость есть результат приложенной (заданной) разности температуры. Возможный набор единиц измерения есть: расстояния - характерный размер L , температуры - характерная разность температур θ , скорости - величина ν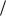 L , времени - L2
L , времени - L2 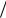 ν è
ν è
давления - ρ0ν 2 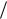 L2 . П ереходя к безразмерным величинам, получаем систему уравнений
L2 . П ереходя к безразмерным величинам, получаем систему уравнений

30
¶v |
|
|
r r |
|
|
|
r |
|
r |
|
|
|
+ |
(vÑ )v |
= - Ñ P + |
Dv |
+ |
GTez |
, |
||||
¶t |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
¶T |
|
|
r |
|
1 |
|
|
|
|
|
|
|
|
+ |
(vÑ )T = |
|
DT , |
|
|
|
(1.26) |
||
¶t |
|
σ |
|
|
|
||||||
|
r |
= 0. |
|
|
|
|
|
|
|||
div v |
|
|
|
|
|
|
|
||||
В уравнения входят два безразмерных комплекса: число Грассхофа
G =
gβϑL3
ν 2
и число П рандтля
σ = ν .
χ
Число Грассхофа характеризует отнош ение архимедовых сил к вязким и свидетельствуето сильной зависимости конвективных механизмов от размера (в число Грассхофа размер входит в кубе). В отличие от числа Грассхофа, число П рандтля есть физический параметр жидкости, не зависящ ий от конкретной задачи, и характеризую щ ий отнош ение коэффициентов кинематической вязкости и температуропроводности. П риведем несколько типичных примеров значений числа П рандтля. Для газов число П рандтля порядка единицы, у воды σ » 7 , у ртути σ »10− 2 , у глицерина - σ »103 . В жидкостях с малым числом П рандтля теплопередача эффективней конвекции и наоборот, при высоких П рандтлях температура «вморожена» в жидкостьи перенос тепла за счет конвекции становится более эффективен, чем теплопередача.
Н аряду с двумя введенными безразмерными параметрами, в конвективных задачах часто используется число Релея, являю щ ееся произведением чисел П рандтля и Грассхофа
Ra = σG = gβϑL3 .
νχ
Если за единицу скорости взять величину χ 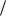 L , оставив всеостальныеединицы измерения прежними, то мы придем к системе уравнений, содержа- щ ей число Релея
L , оставив всеостальныеединицы измерения прежними, то мы придем к системе уравнений, содержа- щ ей число Релея
|
¶v |
|
r r |
|
r |
|
r |
|
|
|
|
|
+ |
(vÑ )v |
= - Ñ P + |
Dv |
+ |
RaTez |
, |
|
¶t |
||||||||
|
|
|
|
|
|
|
|
||
|
|
¶T |
r |
|
|
|
|
|
|
σ |
|
|
+ (vÑ )T = DT , |
|
|
|
(1.27) |
||
|
¶t |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
= 0. |
|
|
|
|
|
div v |
|
|
|
|
|
||||
