П.Г.Фрик - Турбулентность модели и подходы, часть 1

91

Рекомендуемая литература ко второй главе:

1.БержеП ., П омо И ., Видаль Л. П орядок в хаосе. М осква: М ир. 1991. 366с.

2.Ш устер Г. Детерминированный хаос. М осква: М ир. 1988. 240с.

3.Странные аттракторы. Сборник статей. Серия «М атематика. Н о- воев зарубежной науке», выпуск 22. М осква: М ир. 1981. 254с.

92

3 ПОЛУЭМ П И РИ Ч ЕСК И Е М ОДЕЛИ

3.1 Развитая турбулентность

3.1.1Вводныезамечания

Âданной главе мы начинаем рассматривать подходы к описанию развитой турбулентности, то есть течений, возникаю щ их при значительном превышении критических значений управляю щ их параметров (числа Рейнольдса, если речь идетоб изотермическом течении в отсутствии дополнительных силовых полей). Такие течения характеризую тся наполненными спектрами Ф урье, причем нетолько временными, но и пространственными.

Íапомним ещ е раз, что именно в этом и есть основное отличие турбулентности от хаоса в динамических системах невысокого порядка: в турбулентном потоке хаос и пространственный, и временной, а хаотическое поведениемаломодовых систем (соответствую щ их например конвективным тече- ниям при невысокой надкритичности) представляет собой хаотическую во времени эволю цию мод с относительно простой пространственной структурой.

Ïриступая к рассмотрению развитых турбулентных течений, следует сделать ряд важных замечаний. П ервое из них касается уравнений движения жидкости. В первой главе мы получили уравнения Н авье-Стокса, как основныеуравнения, с помощ ью которых мы описываем в дальнейш ем все течения жидкости. Снова подчеркнем, что мы действительно продолжаем считать, что эти уравнения описываю т течения жидкости и в турбулентном режиме, даже при экстремально больш их значениях безразмерных параметров (более того, мы будем рассматривать только случай несжимаемой жидкости). Уверенность в том, что это возможно, держится на результатах многочисленных успеш ных попыток использования этих уравнений для турбулентных течений. Сама возможность приложения уравнений Н авьеСтокса к турбулентности совсем не очевидна (и продолжает подвергаться критике), так как при их выводе было сделано достаточно сильное предположение о том, что тензор вязких напряжений включает в себя только линейные комбинации первых производных поля скорости. В ламинарных и слабо надкритических течениях это предположение кажется разумным и прекрасно работает, но в сильно нелинейных режимах нельзя исклю чить, что тензор вязких напряжений будетиметь болеесложную зависимость от структуры поля скорости. Оправданием использованию уравнений движения в принятой формеможетслужить только сопоставление результатов их реш ения с экспериментальными данными.

95

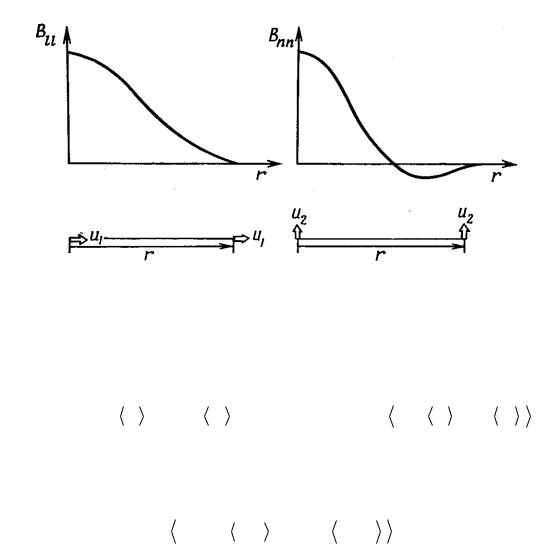
С точки зрения описания турбулентных полей, необходимы статисти- ческие характеристики связи между значениями величины f (r ,t) в различ- ных точках пространства. Это требует введения совместной плотности ве-

Ðèñ.3.1.

роятности P( f (r1 ), f (r2 )) и (или) соответствую щ их двухточечных моментов. Важнейш им среди двухточечных моментов является момент второго порядка, называемый корреляционной функцией

Если речь идет о векторном поле(например, скорости), то появляется корреляционный тензор

Для однородной турбулентности (3.1) и (3.2) зависят только от взаимного расположения двух точек, то есть, если r2 = r1 + r , òî

Важным частным случаем является однородная и изотропная турбулентность, в которой совместная плотностьвероятности (а, следовательно, и двухточечныемоменты) не зависяти от направления вектора r . Тогда

96

Чащ е всего использую т корреляционные функции Bll (r) è Bnn (r) , õà-

рактеризую щ ие корреляцию продольных и поперечных составляю щ их пульсаций скорости. Здесь индексом l обозначена составляю щ ая скорости вдоль линии, соединяю щ ей точки r1 è r2 , а индексом n составляю щ ая, нормальная этой линии. Характерный вид этих функций иллю стрирует рисунок 3.1.

Выш е, в параграфе 2.4.3, указывалось на связь корреляционной функции со спектрами (теорема Хинчина) в случае временного сигнала. Аналогичное соотнош ение связывает и пространственные спектры с двухточечными корреляционными функциями. П режде чем написать это соотнош ение, остановимся несколько подробнее на вопросе о пространственных спектрах турбулентности.

3.1.3П ространственныеспектры

Ïредположим, что рассматриваемое случайное (турбулентное) поле занимает ограниченный объем и величина f (x, y, z,t) можетбыть представ-

лена интегралом Ф урье

r = (x, y, z) - радиус-вектор, k = (k x , k y , k z ) - волновой вектор.

Считая рассматриваемую турбулентность стационарной, определим трехмерный энергетический спектр случайного поля:

Угловыескобки означают в этом случае осреднение по времени. Трехмерный спектр связан с корреляционной функцией B(r ) (теорема Хинчина)

В теории турбулентности, говоря о ее спектральных свойствах, обычно имею т в виду энергетический спектр E(k ) , который характеризует энергию

97

всех гармоник сзаданным модулем волнового вектора, независимо от его направления.

E(k) = òF (k )dk , (3.9)

r

|k |

или, в сферической системе координат,

2ππ r

E(k) = òòF (k )k 2 sinϑ dϑ dϕ .

00

Âважном частном случае изотропной турбулентности, когда F (k ) = F (k) , связьстановитсяочень простой:

Отметим, что всеоценки для спектральных законов развитой турбулентности касаютсяобычно именно энергетического спектра E(k ) .

Если в турбулентном потоке измерения проводятся вдоль одной прямой, то по этим измерениям можно построить одномерное фурьепреобразование. Ограничиваясь однородной и изотропной турбулентно-

Квадрат модуля этой величины есть одномерный энергетический спектр

Чтобы получить связь между одномерным и трехмерным спектрами, выразим исходную величину на прямой y = z = 0 через обратное преобразо-

ваниеФ урье. С одной стороны

98

Таким образом,

В следую щ их главах, рассматривая структуру мелкомасш табной турбулентности, мы постоянно будем обращ аться к спектрам, описываемым степенными законами. П окажем, как связаны между собой введенныеспектры турбулентности при степенной зависимости энергии от масш таба (волнового числа). П усть имеется однородное изотропное поле скалярной величины, энергетический спектр которой следует степенному закону

E(k) ~ k α .

Тогда трехмерный спектр

α − 2

F (k) ~ k α − 2 = (k x 2 + k y 2 + k z 2 ) 2 ,

а одномерный

α − 2

F1 (kx ) ~ ò(k x 2 + k y 2 + k z 2 ) 2 dk y dk z =

закону, а степень убывания трехмерного спектра меньш е на двойку (т.е. трехмерный спектр значительно круче).

100

В уравнение Рейнольдса для средних полей входит одноточечный корреляционный тензор пульсаций скорости, называемый тензором напряжений Рейнольдса

Этот тензор нельзя выразить через осредненные характеристики турбулентных полей. Следовательно, число неизвестных превышает число имею щ ихся уравнений и система (3.19)-(3.20) являетсяне замкнутой.

3.2.2Ц епочка уравнений Ф ридмана-Келлера и проблема замыкания

Âуравнении Рейнольдса появиласьновая неизвестная величина - тензор напряжений Рейнольдса (3.21), для которого также можно получить эволю ционное уравнение. Так как

∂tτij = ∂t ui u j = ui ∂t u j + u j ∂t ui ,

то сначала требуется получить уравнение для пульсаций скорости, для чего из уравнения (3.17) необходимо вычесть уравнение (3.19). П олучим (немые индексы j заменены на k )