
Московский государственный университет имени М.В. Ломоносова, физический факультет.
Реактивное движение
курсовая работа по курсу
компьютерные методы физики студента 214 группы
Пяткина Юрия Константиновича.
Преподаватель –
Шленов Святослав Александрович.
Москва, 2003.
В данной курсовой работе рассматривается конкретный случай реактивного движения – старт ракеты с поверхности планеты и набор (или не набор) ею второй космической скорости. Рассмотрение этого процесса производилось с помощью соответствующей программы, моделирующей его. В разделе теория рассмотрен принцип реактивного движения и необходимые формулы. В разделе модель рассмотрены используемые допуски, приближения и численные методы. В разделе анализ результатов представлены результаты, полученные в результате компьютерного моделирования, в том числе необходимые условия для придания фиксированной полезной нагрузке второй космической скорости при старте с различных тел Солнечной системы.
Теория.
Реактивное движение – движение тела переменной массы, где тяга создается в результате отброса части массы, принадлежащей телу.[1]
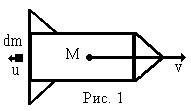 Рассмотрим
конкретный случай реактивного движения
– полет ракеты. Пусть в некоторый момент
времени ракета имеет массу M(t)
и скорость
Рассмотрим
конкретный случай реактивного движения
– полет ракеты. Пусть в некоторый момент
времени ракета имеет массу M(t)
и скорость![]() .
Пусть ракета отбрасывает массу dM' со
скоростью
.
Пусть ракета отбрасывает массу dM' со
скоростью
![]() (см.
рис. 1). Если dM’
– отбрасываемая масса, то dM
– изменение массы ракеты. По закону
сохранения массы
(см.
рис. 1). Если dM’
– отбрасываемая масса, то dM
– изменение массы ракеты. По закону
сохранения массы
dM + dM’ = 0 (1).
Очевидно, что dM
< 0, т.е.
масса самой ракеты уменьшается. В момент
времени t
(до отброса части массы) полный импульс
системы равен
M![]() .
А в момент времени t
+ dt (после
отброса части массы) он
равен
.
А в момент времени t
+ dt (после
отброса части массы) он
равен
![]() .
По закону
сохранения импульса получим
.
По закону
сохранения импульса получим
![]() (2).
(2).
Перемножив скобки
и отбросив член
![]() (в силу того, что он - бесконечно малый
член второго порядка малости) получим
следующее уравнение:
(в силу того, что он - бесконечно малый
член второго порядка малости) получим
следующее уравнение:
![]() (3).
(3).
Учитывая закон сохранения массы (1) получим из (3) уравнение движения:
![]() (4).
(4).
Если скорости
![]() и
и
![]() достаточно малы (т.е. существенно меньше
скорости света), то можно воспользоваться
приближением классической механики
для
достаточно малы (т.е. существенно меньше
скорости света), то можно воспользоваться
приближением классической механики
для
![]() :
:
![]() (5),
(5),
где
![]() - скорость отброшенной массы относительно
ракеты. Если подставить (5) в (4) и
продифференцировать левую часть (4) по
времени, получим уравнение
- скорость отброшенной массы относительно
ракеты. Если подставить (5) в (4) и
продифференцировать левую часть (4) по
времени, получим уравнение
![]() (6),
(6),
описывающее
движение ракеты с нерелятивистскими
скоростями в отсутствие внешних сил.
Введя
![]() (т.е. расход топлива) и
(т.е. расход топлива) и
![]() -
совокупность
внешних сил, действующих на ракету,
– получим итоговое уравнение движения:
-
совокупность
внешних сил, действующих на ракету,
– получим итоговое уравнение движения:
![]() (7).
(7).
Рассмотрим теперь
более конкретный случай: прямолинейное
движение ракеты с постоянной скоростью
отброса газов относительно нее
![]() ,
причем
,
причем
![]() направлена
так,
чтобы
ракета разгонялась. Предположим также,
что на ракету не действуют внешние силы.
Тогда уравнение движения принимает
вид:
направлена
так,
чтобы
ракета разгонялась. Предположим также,
что на ракету не действуют внешние силы.
Тогда уравнение движения принимает
вид:
![]() (8),
(8),
знак “-“ в правой части уравнения обусловлен тем, что при разгоне ракеты v и u’ противоположно направлены. Пусть v0 – скорость ракеты перед началом ускорения, а М0 – начальная масса ракеты. Если переписать уравнение (8) в виде
![]() (9),
(9),
то, проинтегрировав (9), получим формулу, называемую формулой Циолковского:
![]() (10).
(10).
Формула Циолковского может быть преобразована для определения конечной скорости ракеты:
![]() (11).
(11).
Кроме того, для рассмотрения данной задачи необходимо ввести две физические характеристики места старта ракеты: ускорение свободного падения и вторая космическая скорость.
Ускорение свободного падения – ускорение, которое приобретает тело в поле силы тяжести данного небесного тела. Пусть небесное тело (для определенности – планета) обладает массой Mp и радиусом Rp. Согласно закону всемирного тяготения между планетой и телом массы m, находящимся от центра масс планеты на расстоянии x, возникает сила притяжения
![]() (12),
(12),
где G
= 6.672![]() 10-11
Н
10-11
Н![]() м2/кг2
– гравитационная постоянная. Согласно
второму закону Ньютона действующая на
тело массы m
сила
м2/кг2
– гравитационная постоянная. Согласно
второму закону Ньютона действующая на
тело массы m
сила
![]() (13).
(13).
Приравнивая правые части (12) и (13) и сокращая их на m, получим выражение для g:
![]() (14).
(14).
Если h – высота тела над поверхностью планеты, то x=R+h. Таким образом, из (14) получим зависимость g от высоты h:
![]() (15).
(15).
Вторая космическая скорость – скорость, которую необходимо придать телу, чтобы оно могло покинуть планету и удалиться от нее на бесконечно большое расстояние, т.е. скорость, при которой кинетическая энергия ракеты превысит потенциальную энергию ракеты, обеспечиваемую полем силы тяжести. Соответствующее равенство выражается формулой:
![]() (16).
(16).
Сокращая правую и левую части (16) на m и учитывая выражение для g (15), получим формулу для второй космической скорости на высоте h:
![]() (17).
(17).
