Московский государственный университет имени М. В. Ломоносова физический факультет

Колебания маятника с переменной длиной

Курсовая работа по курсу “Компьютерные методы физики” Студента *** группы ***

Преподаватель: ***

Москва, 2004 г.

Задание

Выполнить компьютерное моделирование колебаний маятника с изменяющейся по гармоническому закону длиной. Рассмотреть предельные случаи и общий случай. Продемонстрировать графики траектории и фазового портрета для каждого из рассматриваемых случаев.

Введение.

Рассматривается модель математического маятника. Нить нерастяжима и невесома.

Ускорение свободного падения постоянно и равно g=9,8. На маятник не действуют другие тела, кроме Земли.

Теория.

Рассмотрим основные закономерности собственных колебаний математического маятника с переменной длиной. Пусть в начальный момент длина маятника L=30, координата x=0 и скорость v=0 (все уравнения написаны в системе СИ).

Пусть, далее, частота изменения длины маятника равна ₁ радиан в секунду. Длину в конкретный момент времени обозначим как l₁. Тогда длина маятника будет изменяться по закону:

l₁=L*(2+cos(₁*t+)),

где t-время в секундах,

-начальная фаза изменения длины в радианах.

Обозначим мгновенную частоту колебаний маятника за ₂. Ее можно вычислить, пользуясь формулой Томпсона:

,

откуда

При постоянной длине маятника колебания маятника будут происходить по закону:

,

где X-амплитуда колебаний,

-декремент затухания.

Добавим в это уравнение член, соответствующий изменению длины маятника, который можно легко получить из геометрических соображений:

Получим:

Эти колебания не являются периодическими, однако условно периодом таких колебаний считается T=2π/₂.

При увеличении трения период колебания увеличивается. При большом трении движение вообще перестает быть колебательным, принимая вид экспоненциальной функции.

[рис. 1]

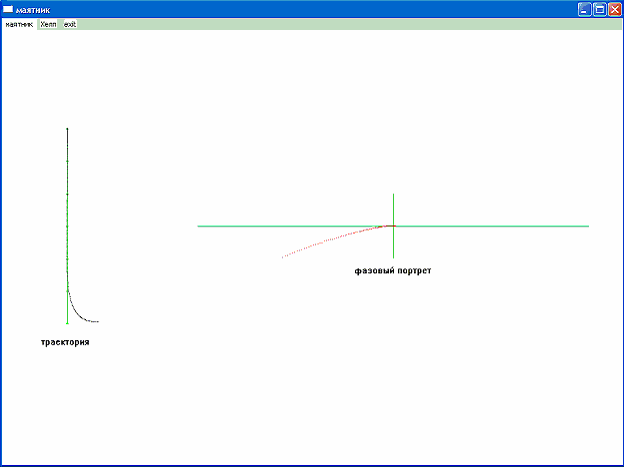
Численные методы.

Представим колебания данного маятника в виде задачи Коши:

,

где ,

Выберем на отрезке [,X] некоторую сетку {x_n, } значений аргумента так, чтобы. Разлагая решение u(x) по Тейлору на интервале сетки и обозначая , получим

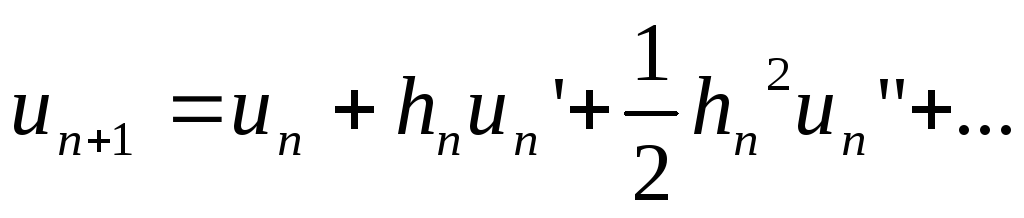, (1)

где

Ограничась первым членом разложения, получим схему ломаных:

(2)

При такой замене можно найти только приближенные значения функции в узлах. Будем обозначать эти значения через в отличие от точных значений . Для численного расчета по схеме ломаных достаточно задать начальное значение . Затем по формуле (2) последовательно вычисляем величины .

Полагаем непрерывной и ограниченной вместе со своими производными:

,

откуда

.

Обозначим ошибку на n-ном шаге .

Вычитая из (1) (01) получим

(3)

Погрешность на произвольном шаге

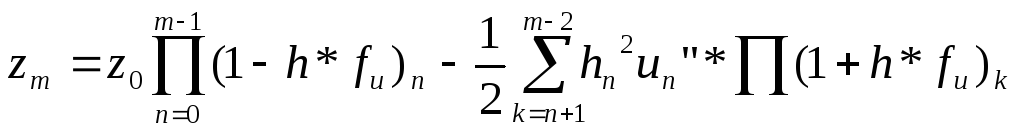
При малых шагах сетки

,

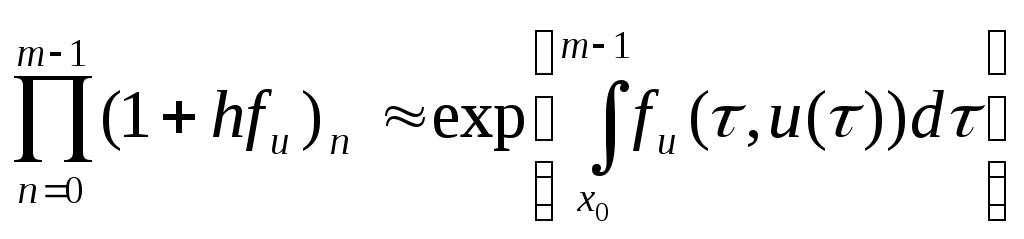причем в качестве верхнего предела можно взять , т.к. ошибка при этом остается в пределах общей точности преобразований.

Аналогично преобразуя второй член, получим

,

где h(x) – непрерывная функция, дающая

в каждом узле x_n величину шага h_n.

Чтобы найти положение маятника в любой момент времени, применим метод Эйлера [2] для нахождения решения

где d – шаг сетки. Метод Эйлера основан на замене производной разностным отношением по приближенной формуле

Δx/Δt= f(t,x),

где

Δx= x(t + d)-x(t), Δt=(t +d) – t.

Приближенные значения y_k в точках x_k=x₀ + kh вычисляются по формуле

x_k+1=x_k + hf(t,x) (k=0,1,2,3,…,n)

Применим данный метод для вычисления положения маятника. Пусть в начальный момент времени t₀=0. Пусть при t₀ =0 маятник находился на расстоянии X от положения равновесия: х₀ = X. Тогда через интервал времени d маятник будет находиться в точке

Положив шаг равным 0.01, мы получим достаточную степень точности для данных условий (X=10, =0,05).

Формулы, использованные в этом разделе, взяты из [2], с. 244.

Результаты.

Рассмотрим случай, когда трение среды, в которой колеблется маятник равно нулю и его длина не изменяется. Тогда видно, что маятник будет совершать обыкновенные гармонические колебания.

[рис. 1]

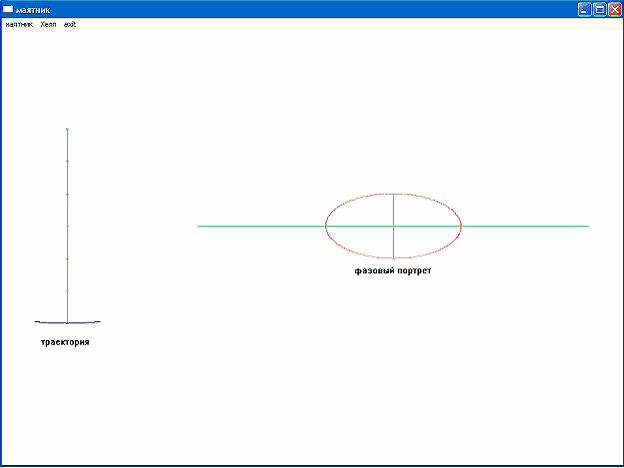
Пусть теперь длина маятника начнет изменяться, а затухание остается равным 0. Тогда координата у будет зависеть не только от ₂, но и от ₁:

[рис. 2]

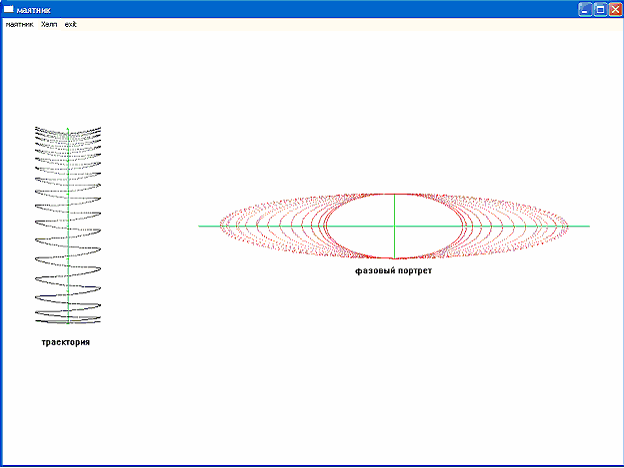
(Частота изменения длины ₁=0,1)

Теперь рассмотрим наиболее общий случай: присутствует трение и изменяется длина и, соответственно, частота колебаний маятника. Амплитуда колебаний будет ограничена экспонентой, характеризующей затухание:

[рис3]

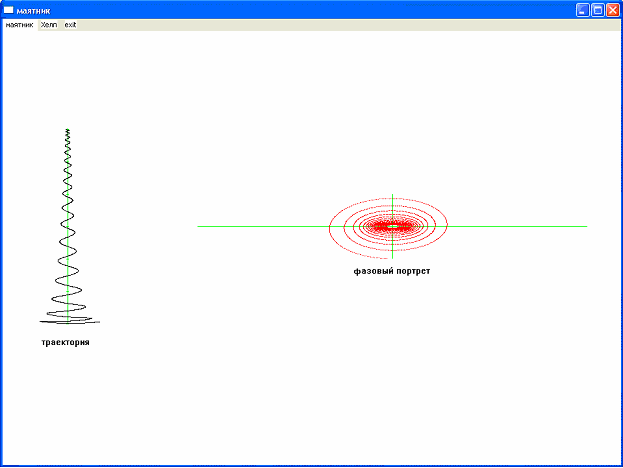
(=0,1; ₁=0,1)

Оставим условия предыдущего опыта, но увеличим частоту изменения длины маятника:

[рис 4]

(=0,1; ₁=0,5)

Как видно из рисунков, результаты вполне совпадают с ожидаемыми, что подтверждает правильность сделанных расчетов.

Литература.

1. Матвеев А.Н. Механика и теория относительности. М.: Высш. шк. 1986.

2. Калиткин Н.Н. Численные методы: учебное пособие для студентов. М.: Наука, 1978.