II курс - курсовые / Движение в центральном поле / test / centr_pole

13

Московский государственный университет имени М.В. Ломоносова Физический факультет

Движение в центральном поле

Курсовая работа по курсу “компьютерные методы в физике ”

Студента 214 группы Недялкова А

Преподаватель: доцент C.A.Шленов

Москва-2003.

Цель работы: Смоделировать движение тела в центральном поле с потенциалом

U=. (1)

Проверить закон сохранения полной энергии, а также второй закон Кеплера. Смоделировать движение при  отличных от нуля ().

Теоретическое введение.

Поле, в котором потенциальная энергия зависит только от расстояния r до определенной неподвижной точки, называют центральным^[1].

Сила

, (2)

действующая на частицу, по абсолютной величине зависит при этом тоже только от и направлена в каждой точке вдоль радиус-вектора.

При движении в центральном поле сохраняется момент количества движения системы относительно центра поля. Для одной частицы это есть

. (3)

Поскольку векторы и взаимно перпендикулярны, постоянство означает, что при движении частицы ее радиус-вектор все время остается в одной плоскости – плоскости, перпендикулярной . Таким образом, траектория движения частицы в центральном поле лежит целиком в одной плоскости.

Введя полярные координаты r и , напишем закон сохранения момента

. (4)

Для плоского движения одной частицы центральном поле этот закон допускает простую геометрическую интерпретацию. Выражение представляет собой площадь сектора, образованного двумя бесконечноблизкими радиус-векторами и элементом дуги траектории (рис 1).

Рис 1. Геометрическая интерпретация закона сохранения момента количества движения.

Обозначив ее как , напишем момент частицы в виде

, (5)

где производную называют секториальной скоростью. Поэтому сохранение момента означает постоянство секториальной скорости – за равные промежутки времени радиус-вектор движущейся точки описывает равные площади (второй закон Кеплера)^[1].

Полное решение задачи о движении частицы в центральном поле проще всего получить, исходя из законов сохранения энергии и момента. Выражая через M из (4) и подставляя в выражение для энергии, получим^[1]:

. (6)

Отсюда

(7)

или, разделяя переменные и интегрируя:

(8)

Далее, написав (4) в виде

(9)

подставив сюда из (7) и интегрируя, находим:

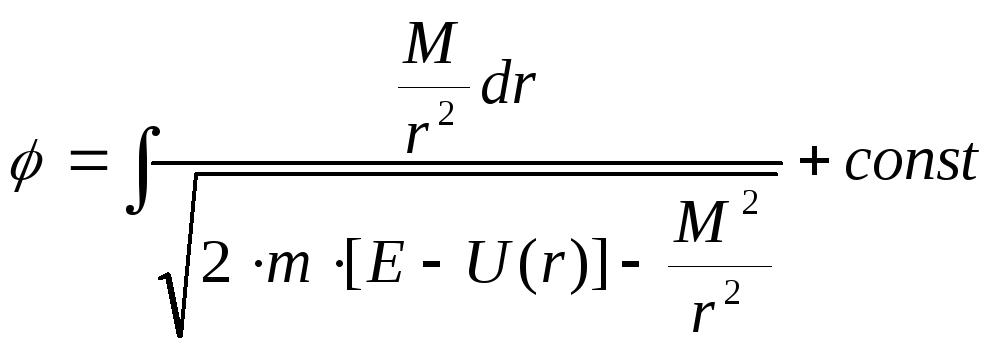(10)

Формулы (8), (10) решают поставленную задачу в общем виде. Вторая из них – уравнение траектории^[1].

Если область допустимого изменения r ограничена лишь одним условием , то движение инфинитно. Если область изменения имеет две границы r_min и r_max (E<0)_, то движение является финитным и траектория целиком лежит внутри кольца, ограниченного окружностями r=r_min и r=r_max (рис 2). Это, однако, не означает, что траектория непременно является замкнутой кривой. За время, в течение которого r изменяется от r_min до r_max , затем до r_min , радиус вектор повернется на угол , равный

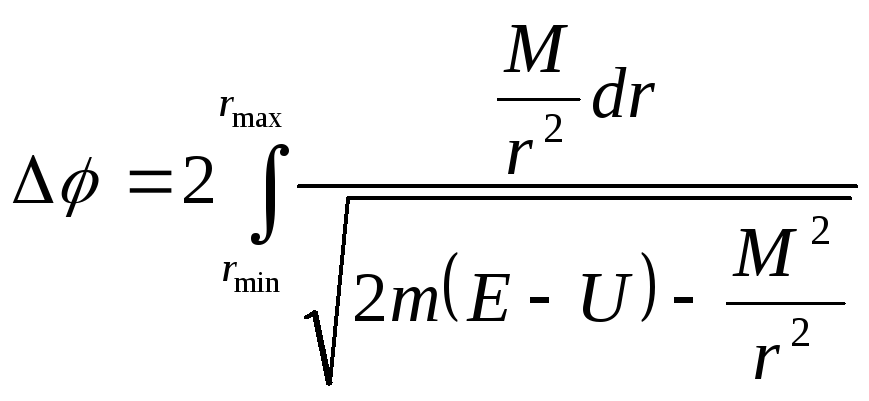. (11)

Если , где m,n целые числа, тогда через n повторений этого периода времени радиус-вектор точки, сделав m полных оборотов, совпадет со своим первоначальным значением, т.е. траектория замкнется. Однако такие случаи исключительны. Поэтому при U=, траектория финитного движения не замкнута (рис 2). Она бесчисленное число раз проходит через минимальное и максимальное расстояние и за бесконечное время заполняет все кольцо между двумя граничными окружностями.

Важнейшим случаем центральных полей являются поля, в которых потенциальная энергия обратно пропорциональна r и соответственно силы обратно пропорциональны r². Сюда относятся ньютоновские поля тяготения и кулоновские электростатические поля. Первые, как известно, имеют характер притяжения, а вторые могут быть как полями притяжения, так и отталкивания.

Рассмотрим поле притяжения, с потенциалом

(12)

и положительной постоянной А. Форму траектории можно получить с помощью формулы (10). Подставляя в нее (12) и производя элементарное интегрирование, получим:

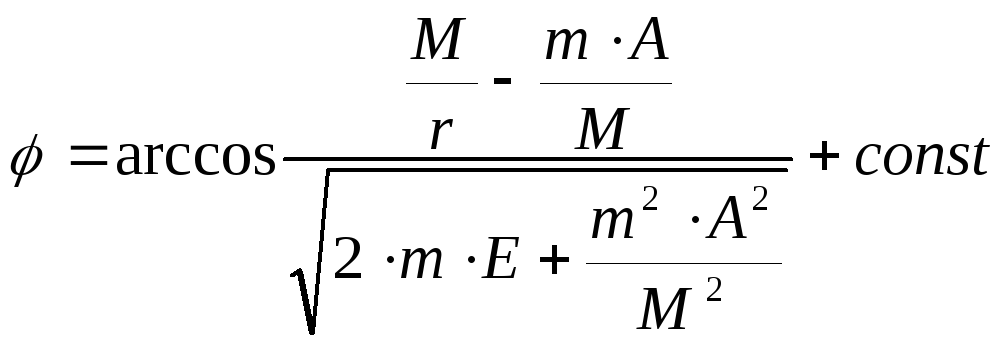. (13)

Выбирая начало отсчета угла так, чтобы const=0, и вводя обозначения

,, (14)

перепишем формулу траектории в виде

. (15)

Это есть уравнение кривой второго порядка, в фокусе которой находится начало координат; p и e – параметр и эксцентриситет орбиты.

Из (15) видно, что при E<0 эксцентриситет e<1, орбита является эллипсом и движение финитно. При e=0 эллипс обращается в окружность. При E₀  0 движение инфинитно. Если E₀ > 0, то эксцентриситет e > 1, т.е. траектория является гиперболой, огибающей центр поля (фокус). В случае же E₀ > 0 эксцентриситет e = 1, т.е. частица движется по параболе^[1].

Численное решение.

Без ограничения общности введем декартовы координаты x и y так, что бы центром поля была точка (0,0). Запишем согласно (1) и (2) второй закон Ньютона для частицы и начальные условия:

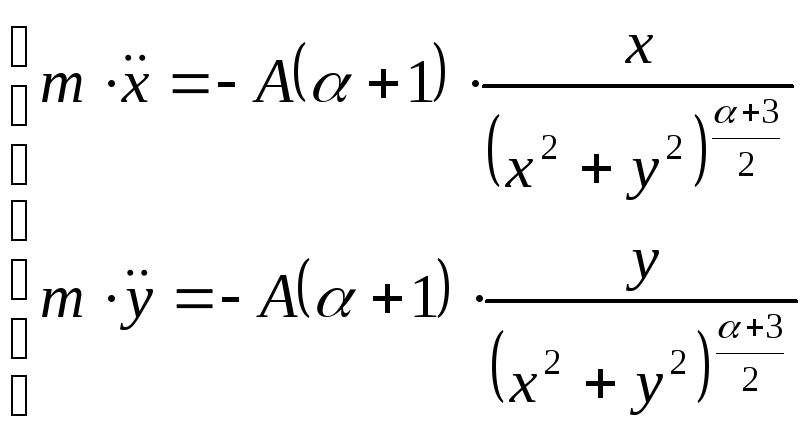, (16)

. (17)

Произведем обезразмеривание величин, вводя новые переменные

. (18)

Получим

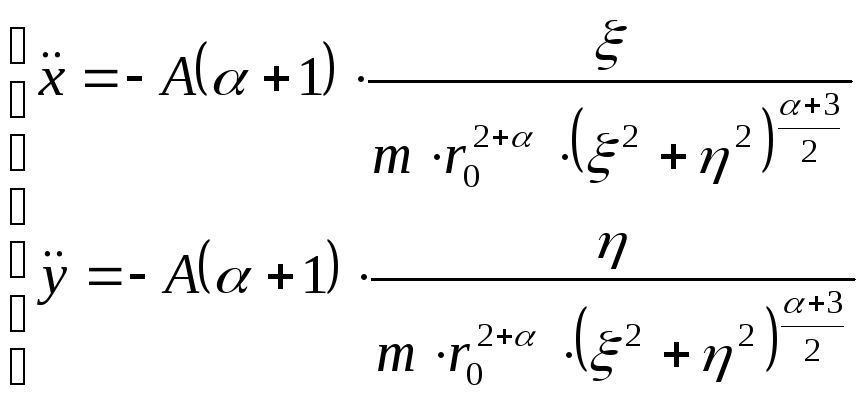. (19)

Учитывая, что

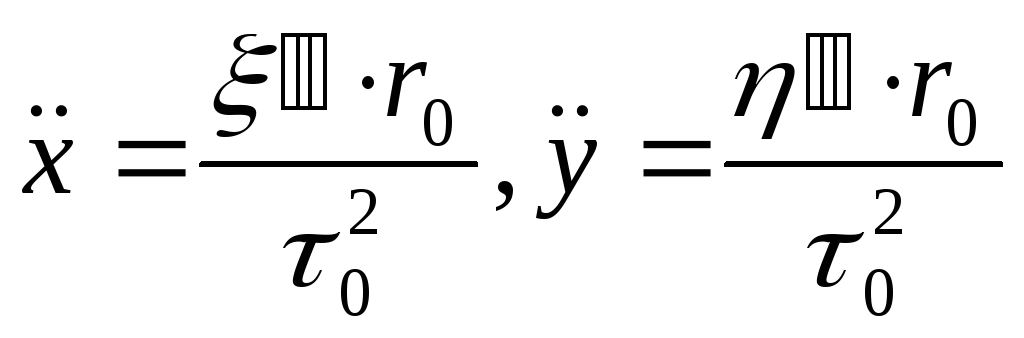, (20)

находим

, (21)

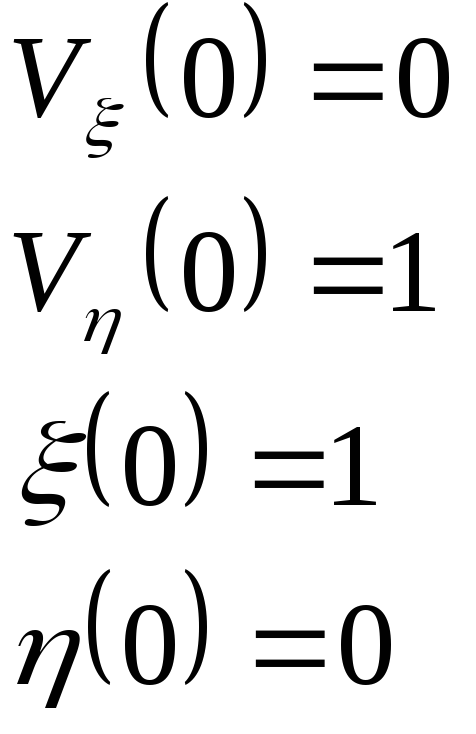, (22)

где . (23)

Для численного решения системы обыкновенных дифференциальных уравнений (21) , удовлетворяющей начальным условиям (22) применим метод Рунге-Кутта четвертого порядка. В обобщенном виде система уравнений, совместно с начальными условиями могут быть записаны в векторной форме:

, (24)

где - вектор-столбец искомых решений, – вектор-столбец всей правой части системы^[3]. Численное решение на (n+1) шаге интегрирования (в момент времени ) выражается через решение на n шаге в виде:

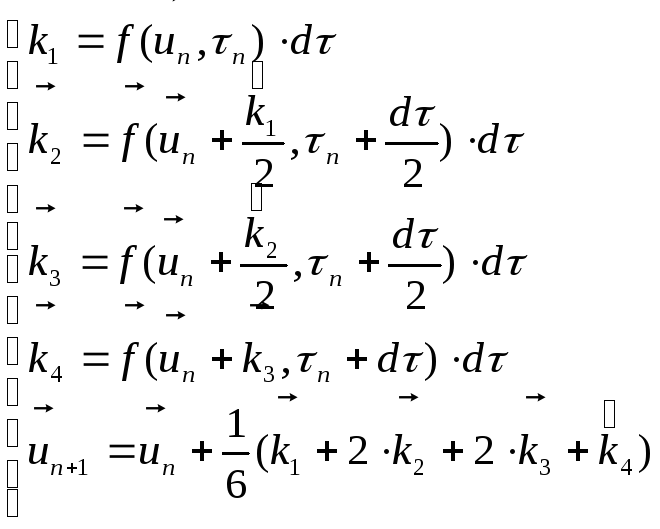. (25)

Обсуждение результатов.

Если E_полн <0, то движение финитно. На рисунках 2,3,4 показаны траектории соответствующие полям с различными значениями при равных отрицательных полных энергиях частиц. При траектория целиком лежит внутри кольца и не является замкнутой. За время, в течение которого r изменяется от до , затем до , радиус вектор повернется на некоторый угол (рис 2). При начальных условиях (22) радиус вектор повернется по часовой стрелке в случае (рис 2) и против часовой стрелки при (рис 3). При траекторией является эллипс (рис 4).

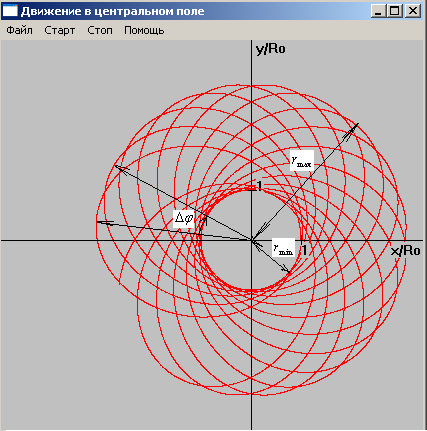
Рис 2. Траектория движения при W=0.7, (E_полн<0).

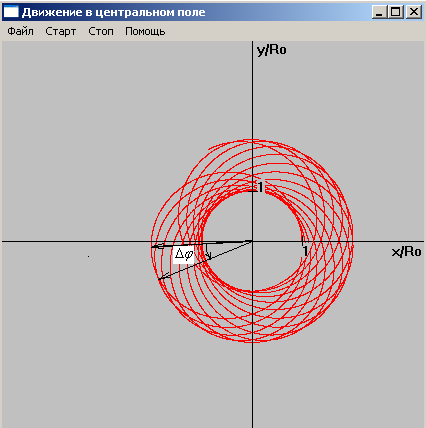
Рис 3. Траектория движения при W=0.7, (E_полн<0).

Рис 4. Траектория движения при W=0.7, (E_полн<0). Закрашенные сектора иллюстрируют второй закон Кеплера.

Если , то движение инфинитно. При Е_полн=0, движение происходит по параболе (рис 5). Для случаев, когда E=0, траектория показана на рисунках 6,7.

При траектория - гипербола (рис 8). Для случаев, когда E_полн>0, траектория показана на рисунках 9,10.

На рисунках 11,12,13 представлены графики зависимости энергии от времени при различных значениях полной энергии. На них видно выполнение закона сохранения полной энергии. При более детальном изучении, установлено, что полная энергия меняется примерно на 10^-9 % за период (в случае движения по эллипсу). Это связано с погрешностью численного метода и ошибкой округления.

На рисунках 4,5,6 демонстрируется выполнение второго закона Кеплера. За равные промежутки времени радиус-вектор движущейся точки описывает равные площади.

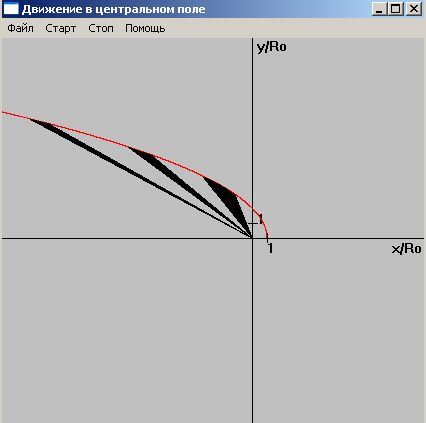
Pиc 5. Траектория движения при W =0.5, (E_полн=0). Закрашенные сектора иллюстрируют второй закон Кеплера.

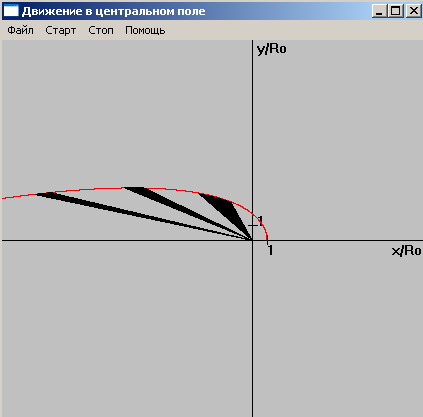
Рис 6. Траектория движения при W=0.5, (E_полн=0). Закрашенные сектора иллюстрируют второй закон Кеплера.

Рис 7. Траектория движения при W=0.5, (E_полн=0).

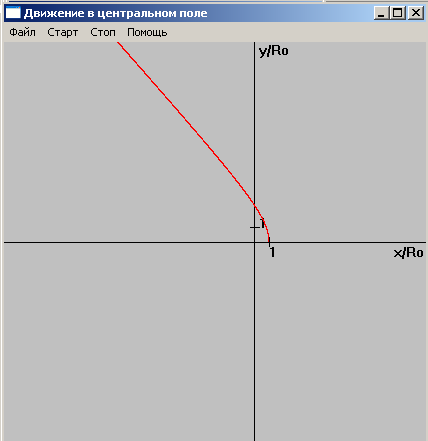
Рис 8. Траектория движения при W=0.4, (E_полн>0).

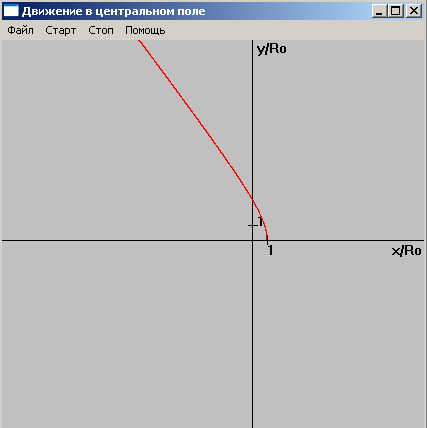
Рис 9. Траектория движения при W=0.4, (E_полн>0).

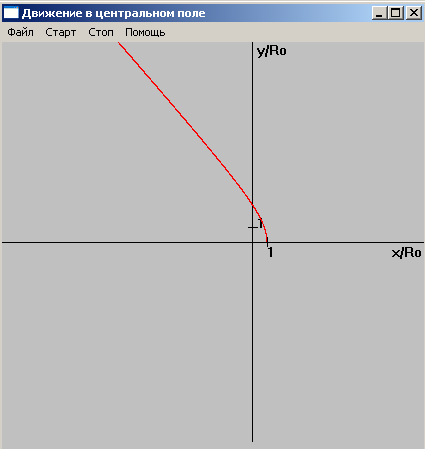
Рис 10. Траектория движения при W=0.4, (E_полн>0).

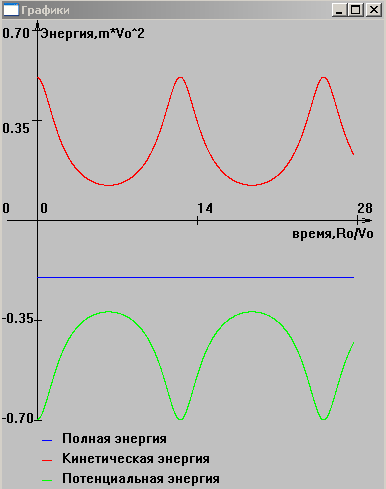
Рис 11. Изменение энергии со временем при W=0.7, (E_полн<0).

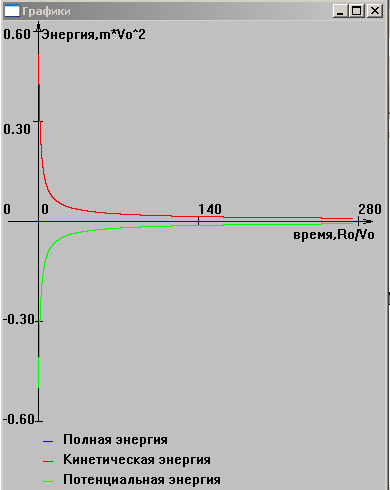
Рис 12. Изменение энергии со временем при W =0.5, (E_полн=0).

Рис 13. Изменение энергии со временем при W=0.4, (E_полн>0).

Литература.

[1] Л.Д. Ландау, Е.М. Лившиц. Теоретическая физика. Механика. Москва, Наука, 1973.

[2] И.И. Ольховский. Курс теоретической механики для физиков. Москва, Издательство московского университета, 1978.

[3] В.И. Приклонский. Численные методы. Москва, Физический факультет МГУ, 1999.