Файловый архив студентов. Файловый архив студентов.
1304 вуза, 5163 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Национальный технический университет Украины «Киевский политехнический институт»
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Bulashenko_C4

.pdf
Скачиваний:
27
Добавлен:
12.05.2015
Размер:
4.03 Mб
Скачать
☆

 

 

 

 

 

 

 

 

Початкові умови в колі ну-

 

 

 

 

 

 

 

 

льові, тобто uC (0 ) uC (0

)

0 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

 

 

 

Розв'язок

диференціального

 

 

 

C

 

E

рівняння (1.11) має вигляд

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

uC (t) uC.ВИМ

uC.B (0 )

Е

еpt ,

 

Рисунок 7.11

 

 

 

 

 

 

 

де uC.ВИМ E – вимушена складова, тобто напруга на конденсаторі після завершення перехідного процесу. Характеристичне

рівняння одержимо методом вхідного опору Z ( p)

0

R

1

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

pC

Звідки p

 

1

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

RC

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Довільну інтегрування знайдемо, використовуючи почат-

кові умови. При t=0+

u

C

(0 ) 0

u

 

 

(0 ) u

C.B

(0

)

Aе0 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C.В И М

 

 

 

 

Звідки A=–E.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Отже,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

t

 

 

 

 

 

t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u

C

(t)

E Ee RC

E(1 e RC ).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Перехідний струм

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

duC

 

 

E

 

 

t

 

 

 

 

 

 

 

 

 

 

 

i(t)

 

C

 

e RC .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

R

 

 

 

 

 

 

 

 

 

 

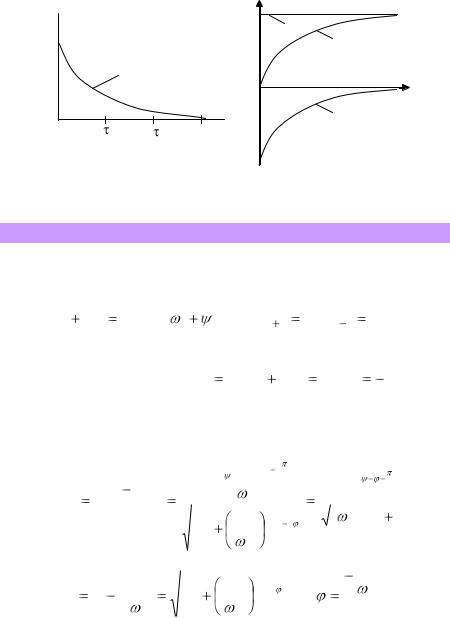
Графіки перехідного струму та напруги на конденсаторі подані на рис. 7.12.

121

uC

i

E

uC.ВИМ

E/R

 

uC(t)

 

 

i(t)

 

 

 

 

t

 

 

uC.В

2

t

 

а)

 

б)

Рисунок 7.12

7.7.5 Включення RС-кола під змінну напругу

Диференціальне рівняння та початкові умови кола аналогічні рівнянню (7.11)

RC

duC

uC

U m sin( t ), uC (0 ) uC (0 ) 0.

dt

 

 

 

Аналогічно попередньому випадку визначається та корень хара-

ктеристичного рівняння Z ( p) 0; R

1

0; p

1

.

 

 

 

pC

 

RC

Вимушена складова напруги на конденсаторі uC.ВИМ, тобто та напруга, яка встановиться після завершення перехідного процесу, розраховується спочатку в комплексній формі

 

 

 

 

U m e j

1

 

e j

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

j (

 

)

 

 

 

( jxС )

 

 

 

 

 

U m e

2

 

C

 

 

U m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U C m .ВИМ

 

Z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

, де

 

 

 

 

 

1

 

2

 

 

 

 

 

( CR)2

1

 

 

 

 

 

R 2

 

 

 

e j

 

 

 

 

 

 

 

 

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

1

 

 

1

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C

 

Z R j

 

R2

e j , tg

 

,

 

 

 

 

 

C

 

 

C

 

 

 

R

а потім записується його миттєве значення

122

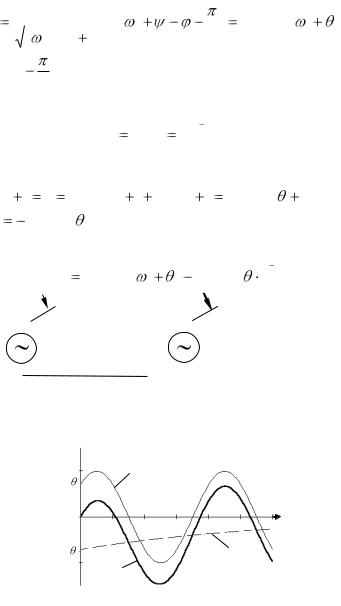
uCпп

 

U m

 

 

sin( t

 

) UCm sin( t ) ,

 

 

 

 

2

( CR)2

1

 

 

 

 

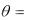
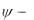
де 2 .

Вільна складова напруги на конденсаторі має такий вигляд:

 

 

 

 

t

 

 

Ae pt

 

 

 

u

C.В

Ae RC .

 

 

 

 

 

Довільна інтегрування визначається при використанні початкових умов. При t=0+

uC (0

)

 

 

0

 

uC.ВИМ (0 )

uC.B (0 )

uC m sin

Aе0 .

Звідси A

uC msin .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Таким чином,

перехідна напруга на конденсаторі має вигляд

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(рис. 7.13, а):

u

C

(t)

U

Cm

sin( t

) U

Cm

sin e RC .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

E

 

 

R

 

 

 

 

C

 

 

 

E

 

 

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а)

 

 

 

 

 

 

 

 

 

 

 

 

б)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 7.13

 

 

 

 

 

 

 

 

 

 

 

 

 

uC

uC.ВИМ

UC msin

t

-UC msin

uC.В

 

 

uC(t)

Рисунок 7.14

123

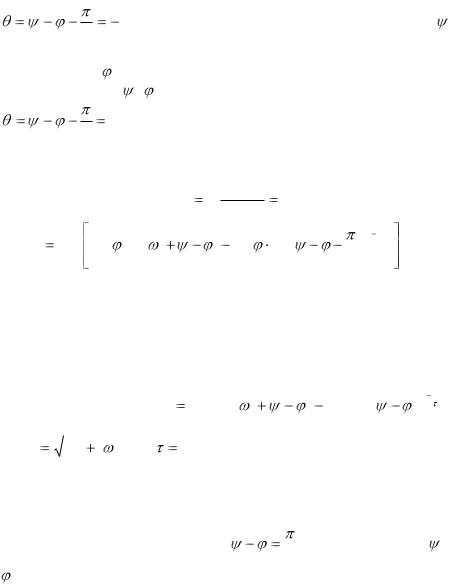
На рис. 7.14 видно, що напруга на конденсаторі uС(t) під час перехідного режиму може перевищити амплітуду ДР напруги на конденсаторі в усталеному режимі Ucm, але не більше ніж в 2 рази. Найбільше перевищення може бути у випадку, коли кут

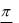або коли початкова фаза напруги мережі

2 2

(обумовлена моментом включення рубильника) дорівнює куту зрушення фаз між напругою й струмом при режимі, що встановився, тобто = . Можливий також випадок, коли кут

0, тоді вільна складова напруги буде дорівнює

2

нулю, і в колі відразу настане режим, що встановився. Перехідний струм у колі дорівнює

i(t) C duC (t) dt

 

Um

 

 

 

 

t

 

 

 

 

 

 

 

 

cos sin( t

) sin sin(

 

)e RC .

 

R

2

 

 

 

 

 

 

Отриманий вираз для струму пояснює виникнення більших поштовхів струму при включенні ненавантаженої лінії електропередачі, що має схему заміщення, подану на рис. 7.13, б.

При включенні RL-кола під синусоїдальну напругу, рівняння та графік перехідного струму будуть мати вигляд, аналогічний рівнянню та графіку напруги на конденсаторі, розгляну-

 

 

 

 

 

 

 

 

U m

 

 

U m

 

 

t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

тому

вище,

тобто i

L

(t)

 

sin( t

)

sin(

)e ,

 

 

 

 

 

 

 

 

 

 

Z

 

Z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

L

 

 

де Z

 

R2

( L)2 ,

 

 

. При цьому,

як і в розглянутому

 

 

 

R

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

вище випадку, струм i(t) під час перехідного режиму може перевищити амплітуду струму im, що встановився, після завершення перехідного режиму, але не більше ніж у 2 рази. Найбільше пе-

ревищення може бути, коли кут

 

. Аналогічно, при –

2

=0 вільна складова струму дорівнює нулю, і в колі відразу наступає, що встановився режим.

124

7.7.6 Розряд конденсатора у RLС-колі

Диференціальне рівняння кола (рис. 7.15) має вигляд

Ri L

di

u

 

0 , оскільки i C

duC

, то

dt

C

dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d 2u

C

 

 

 

du

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

LC

 

 

 

RC

 

 

C

 

uC

0 .

 

 

 

 

 

 

 

 

 

 

 

 

 

dt2

 

 

dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Початкові умови

uC (0 ) uC (0 ) U0 ,

 

 

 

 

 

 

 

 

 

i(0

 

) i(0 )

 

0 , i(0– )=i(0+ )=0.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

 

Характеристичне

рівняння

складемо

 

 

 

 

 

 

 

 

 

методом вхідного опору

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

С

 

 

L

 

 

 

 

Z ( p)

 

 

0, R

pL

1

 

0.

U0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

pC

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 6.9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 7.15

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Корені характеристичного рівняння

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

 

 

R

2

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p1,2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2L

 

 

2L

 

LC

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

можуть бути трьох видів залежно від величини підкореневого виразу.

А. Аперіодичний розряд конденсатора відбувається при

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

1

>0, тобто при R>Rкр,

де Rкр= 2

 

L

 

– критичний

 

 

 

 

 

 

 

 

 

 

 

2L

 

LC

 

 

 

 

 

 

 

 

 

 

 

 

C

 

опір. При цьому корені p1

та p2

різні

 

 

 

 

 

 

 

 

 

 

u

C

(t) u

C.ВИМ

 

u

C.В

0 A e p1t

 

A e p2t

,

 

 

 

 

 

 

 

 

1

 

2

 

 

 

 

 

 

 

i(t) C

duC

 

C( p Ae p1t p

A e p2t ) .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

 

 

1

2

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Враховуючи початкові умови, знайдемо довільні інтегру-

вання A1

та A2. При

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

t 0

uC (0 ) U 0

 

A1

A2, i(0 ) 0 p1 A1

p2 A2 .

Звідси знаходимо константи

125

 

 

 

 

 

 

 

 

 

 

 

A

 

 

 

 

 

p2U0

,

A

 

 

 

 

p1U0

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

p2

p1

2

 

 

 

 

 

p2

 

p1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Таким чином,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u

 

(t)

 

 

U 0

 

 

 

( p

e p1t

p e p2t ),

i(t)

Cp1 p2U0

(e p1t

e p2t ),

C

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p2

p1

2

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

p2

 

 

p1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u

 

(t)

 

L

di

 

 

 

U0

 

( p e p1t

p

e p2t ).

 

 

 

 

 

 

 

 

 

 

L

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

p2

p1

1

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

За цими рівняннями побудуємо графіки, що зображені на

рис. 7.16

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

uL

 

 

 

 

 

 

 

 

 

 

 

 

uC

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U e p1t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U 0 p2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e p1t

 

 

 

 

 

 

 

 

 

 

 

L( p2

p1 )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p2

p1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

uL(t)

 

 

 

 

 

 

 

 

t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

uC(t)

 

 

 

 

 

 

 

 

 

 

t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i(t)

 

 

 

 

 

e p2t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

0

 

 

 

 

 

 

 

 

 

 

 

U0 p1

 

e p2t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

L( p2

 

p1 )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p2

p1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

б)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а)

 

 

 

 

 

 

 

б)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 7.16

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Слід звернути увагу,

що крива u L (t)

перетинає вісь абсцис

у точці,

 

коли

 

 

струм i(t) досягає максимуму.

 

При

цьому

uL (t) L

di(t)

 

0.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Б. Коливальний розряд конденсатора відбувається при

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

 

 

1

, тобто при R

 

Rкр

2

 

L

 

 

. При цьому корені хара-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2L

 

 

 

LC

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

ктеристичного рівняння – комплексно-спряжені

126

 

 

R

 

1

 

 

R

2

 

p1,2

 

j

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2L

LC

2L

 

 

 

 

 

 

R

 

 

 

 

 

 

 

 

 

 

,

 

2

 

2 ,

2

 

 

 

 

0

 

0

 

 

2L

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

j , де

LC1 .

 

 

Перехідна напруга на конденсаторі

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

uC (t)

 

 

uC.ВИМ

 

 

 

 

uC.В

 

0

 

 

Asin(

 

t

 

 

 

) ),

 

а струм

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i(t) C

 

duC

 

 

 

 

 

 

AC

 

 

 

 

 

sin(

 

 

t

)

 

 

cos(

t

 

) .

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Використовуючи початкові умови, визначимо A і

 

 

. При t =0+

 

 

 

 

 

 

 

 

 

 

 

 

 

 

uC (0

)

 

 

 

 

U 0

 

 

 

 

Asin

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i(0

)

 

 

 

AC[

 

 

 

sin

 

 

 

 

 

cos

 

]

 

0.

 

 

 

 

 

 

 

 

Розв’язуючи спільно отриману систему рівняннь, знайдемо

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

sin

 

 

 

 

 

 

 

 

U0

 

;

 

 

 

cos

 

 

 

 

 

 

 

 

 

U0

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A

 

 

 

 

 

 

 

 

 

 

 

 

A

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

U02

 

2

 

U02

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

sin

 

 

 

 

 

 

 

 

 

cos

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A2

 

2

 

 

A2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A

 

U

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

 

 

 

0

,

 

tg

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Таким чином,

u

 

(t)

 

 

U

 

 

 

 

 

0

 

e

 

t sin(

t

 

 

) ,

 

 

 

 

 

 

 

 

 

 

 

 

C

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i(t) C

duC

(t)

CU

 

 

e

 

t

0

 

 

 

 

 

 

sin(

 

 

t

)

 

 

 

cos(

t

)

 

 

dt

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

CU

 

e

 

t

0

 

sin(

 

t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

)

 

e t

sin(

 

t

 

 

 

),

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

L

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

де

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

; tg

 

 

 

 

 

 

 

 

 

 

 

 

 

 

tg(

 

 

 

 

),

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

LC

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u

 

L

di

 

0

 

 

 

 

 

sin(

 

t

 

 

 

)

 

 

 

 

 

 

 

cos(

t

 

 

)

 

 

U0

0

e

t

sin(

t ).

L

dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

127

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

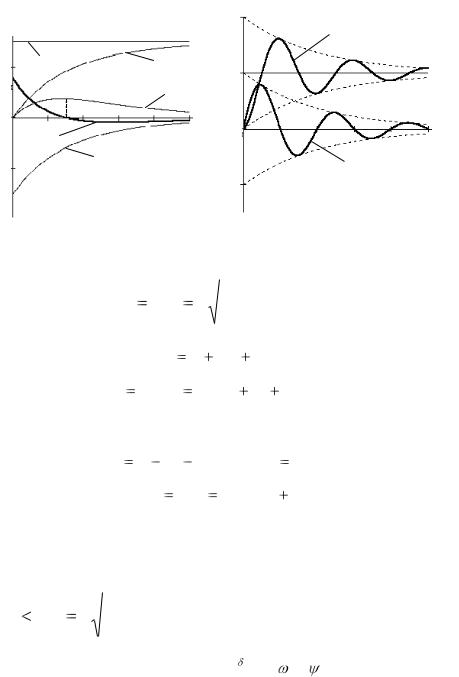
i(t) uC(t)

На рис. 7.17 подані графіки

 

uC(t)

загасаючих коливань i(t), uС(t),

 

побудовані за отриманими вище

 

 

 

 

 

 

рівняннями. Швидкість загасан-

 

 

t

ня таких коливань характеризу-

 

T

 

ють відношенням двох наступ-

 

 

 

 

них амплітуд, яке носить спеціа-

 

 

 

 

 

 

 

 

 

льна назва – декремент коли-

 

i(t)

вань

Рисунок 7.17

 

 

 

 

 

 

 

uC (t)

 

UCт e t sin(

t

)

e

T

.

 

uC (t T )

UCт e (t T ) sin

(t

T )

 

 

 

 

 

Часто використовують і іншу величину, що називають логари-

фмічним декрементом коливань

 

 

 

 

ln

uC (t)

T

 

 

 

 

 

 

 

 

 

uC (t T )

 

 

 

 

 

 

В. Граничний випадок аперіодичного розряду відбува-

 

 

2

 

 

 

 

 

 

 

 

 

 

ється при

R

1

, тобто при R

Rкр

2

 

L

 

та кратними

 

 

 

2L

 

LC

C

 

 

 

 

 

 

 

 

 

 

коренями характеристичного рівняння. У цьому випадку визна-

чають вільну складову напруги на конденсаторі за рівнянням uC . В =(A1 +A2 t)ep t .

При цьому струм

i(t) C

duC

C( A pA pA t)e pt .

 

 

dt

2

1

2

 

 

 

 

При t=0+

uc(0)=U0 =(A1 +0)e0 , i(0)=0=C(A2 +pa1 +0) e0 .

Звідси

А1 =U0 ; A2 =– pa1 =– pu0 ;

uС (t )=(U0 –pu0 t )ep t =U0 (1 –pt )ep t ;

i(t) 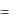Cp 2U 0te pt 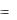UL0 te pt ; 128

u

 

(t) L

di

U

 

(1 pt)e pt .

L

dt

0

 

 

 

 

 

 

 

 

 

 

Графіки цих величин за формою не відрізняються від наведених на рис. 7.17.

7.7.7 Включення RLС-кола під постійну напругу

Диференціальне рівняння кола має вигляд

Ri L

di

uC

E, i C

duC

dt

dt

 

 

 

 

d 2u

C

 

du

 

LC

 

 

RC

C

uC

dt

2

 

dt

 

 

 

 

Початкові умови uС(0+)=0,

i(0+)=0.

 

Примушені складові uС.ВИМ=E,

iВИМ=0.

Характеристичне рівняння Z ( p) 0, R pL

, тобто

E.

10.

pC

Корені цього рівняння, як і у попередньому випадку, можуть бути трьох видів: різні, кратні та комплексно-спряжені. Відповідно

до

цього розглянемо три режими:

 

 

 

 

 

 

 

1. Аперіодичний процес відбувається при

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

R

Rкр

 

2

 

L

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(коли корені різні). При цьому

 

 

 

 

 

 

 

u

 

(t) u

 

 

u

 

 

 

 

E

 

 

E

( p

e p1t p e p2t ) ,

 

C

C.ВИМ

C.В

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p1 p2

2

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i(t) C

duC

 

 

E

 

(e p1t

e p2t ) ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

L( p1

p2 )

 

 

 

 

 

 

 

 

 

 

u

 

 

(t)

L

di

 

 

E

( p e p1t

p

e p2t ) .

 

 

 

 

 

 

 

L

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

p1 p2

1

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

На рис. 7.18, а подані графіки, побудовані за цими рівняннями.

129

uL i

 

 

 

 

 

 

uC, i

 

uC(t)

 

 

 

 

 

 

 

 

 

 

 

 

uC

uC.ВИМ

 

uC(t)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

E

 

 

 

 

 

 

i(t)

 

 

 

 

 

 

 

 

 

uL(t)

 

 

 

 

t

 

 

 

 

 

 

t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

uC.В

 

 

 

 

 

 

 

 

 

 

 

i(t)

 

а)

 

 

 

 

 

 

 

 

 

 

 

б)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рисунок 7.18

 

 

Б. Граничний випадок аперіодичного процесу (критичний)

 

 

 

 

 

 

 

 

 

відбувається при R Rкр

2

 

 

L

 

(коли корені кратні).

 

 

C

 

 

 

 

 

 

 

 

 

 

 

При цьому

 

 

 

 

 

 

 

 

 

 

 

 

 

u

C

(t)

E ( A A t)e pt ,

 

 

 

 

 

1

2

 

 

i(t) C

duC

 

C( A p A A pt)e pt .

 

 

 

 

 

 

dt

 

1

 

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

Використовуючи початкові умови uС(0+)=0, i(0+)=0, визначаємо A1 та A2 аналогічно пункту 1.9

 

uC (t)

 

E

(E Ept)e pt , i(t)

CEp 2te pt ,

 

 

 

 

 

 

u

 

(t)

L

di

LCEp2 (1

pt) .

 

 

 

 

 

 

L

dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Графіки цих рівнянь аналогічні графікам, що зображені на

рис. 7.18, а.

 

 

 

 

 

 

 

 

 

 

 

 

В. Загасаючі коливання відбуваються при

 

 

 

 

 

 

R R

2

 

L

(коли корені комплексно-спряжені).

 

 

 

кр

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

При цьому

 

 

 

 

 

 

 

uС (t )=uC . В И М +uC . В =E+Ae– t sin(

t+ ),

 

 

 

 

 

 

 

 

 

 

 

130

 
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности