Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Konspekt lek. MA-1

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

2.01 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

Лекція 2. Числові функції

Властивості парних і непарних функцій.

1.Зміна знаку перед функцією не змінює її парності (непарності).

2.Сума парних (непарних) функцій є парною (непарною) функцією.

3.Добуток будь-якої кількості парних функцій є парною функцією.

4.Добуток парної функції на непарну є непарною функцією.

Періодичність функції

Означення 2.3 (періодичної функції). Функцію f називають пе-

ріодичною, якщо існує число T 0, таке, що:

1)для кожного x з області означення x T теж належить області означення;

2)виконано рівність

f (x T) f(x).

Число T називають періодом функції f .

Якщо існує найменший додатний період функції, то його назива-

ють основним періодом.
Якщо T — основний період функції f ,		то графік такої функції
«повторюється» з періодичністю T.
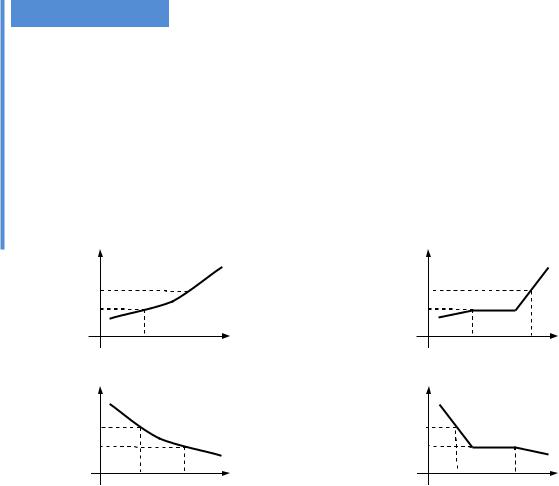
Приміром, функція дробова	частина	y	y	{x}
числа		1	y	{x}
		1

y {x} x [x ]
періодична з основним періодом 1,	а функ-	1 O	1	2 3 x
ція-стала			1
ція-стала		Рис. 2.9. Графік періодичної
f (x) c const, D(f ) .		функції y {x}

періодична, але основного періоду не має.

Властивості періодичних функцій.

1.Якщо T — період функції f , то її періодами також будуть числа mT, m .

2.Якщо функція y f(x), x D(f ), періодична з періодом T, то фун-

кція y f ( x) — періодична з періодом .

22	Розділ 1. Границя функції. Неперервність

Монотонність функції

Означення 2.4 (монотонних функцій). Функцію y f (x), x D,

називають зростаючою (спадною) на множині X D(f ), якщо більшому значенню аргументу з цієї множини відповідає більше (менше) значення функції і позначають f (f ), тобто

x1,x2 X : x1 x2 f (x1) f (x2) (f (x1) f(x2)).

Функцію y f(x), x D(f ), називають неспадною (незростаючою) на множині X D(f ), якщо більшому значенню аргументу з цієї множини відповідає не менше (не більше) значення функції, тобто

	x1,x2 X : x1 x2 f (x1) f (x2)				(f (x1) f(x2)).
y	y1 y2				y	y1	y2
y2	y1 y2				y2	y1	y2
y2					y2
y1					y1
O	x1	x2	x		O		x1	x2 x
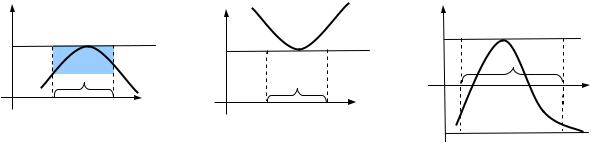
Рис. 2.10. Графік зростаючої функції				Рис. 2.11. Графік неспадної функції
y	y1 y2				y
y1	y1 y2				y		y1 y2
y1					y		y1 y2
					1
y2					y2
O	x1	x2	x		O	x1	x2	x
Рис. 2.12. Графік спадної функції				Рис. 2.13. Графік незростаючої функції

Зростаючі, спадні, неспадні і незростаючі функції називають мо-

нотонними; зростаючі і спадні — строго монотонними.

Стала функцію y c є незростаючою і неспадною водночас. Запишімо означення монотонних послідовностей. Послідовність {xn } :

1)	зростає (позначають {xn } ), якщо
	x1 x2 x3 ... xn xn 1		...		n xn	xn 1;
2)	не спадає, якщо
	x1 x2 x3 ... xn	xn 1	...	n : xn		xn 1;
3)	спадає (позначають {xn } ), якщо

	x1 x2 x3 ... xn	xn 1	...	n : xn		xn 1;
4)	не зростає, якщо
	x1 x2 x3 ... xn	xn 1	...	n : xn		xn 1.

		Лекція 2. Числові функції					23
Монотонність послідовності {an } можна встановити вивчаючи знак
різниці an 1 an або, для послідовностей {bn }							з додатними членами,
порівнюючи відношення		bn 1	з 1.
порівнюючи відношення		bn	з 1.
		bn
	an 1 an			bn 1		Послідовність
	an 1 an				bn	Послідовність
	0			1		зростаюча

	0			1		спадна

	0			1		неспадна

	0			1		незростаюча

Обмеженість функції

(обмеженої функції).

Означення 2.5

Функцію

називають обмеженою

зверху

(знизу) на множині

X D(f )

якщо існує таке число M (m ), що для будь-яких

значень аргументу x X виконано умову

f (x) M (m f (x)).

Функцію f

називають обмеженою на множині X D(f ), якщо існує

таке число C 0, що для будь-яких значень аргументу x X вико-

нано умову

f(x)

Приміром, функція y x2

є обмеженою знизу на своїй природній об-

ласті означення і необмеженою зверху; функція y 2 x2

обмежена

зверху і необмежена знизу на ; функція y sin x є обмеженою на .

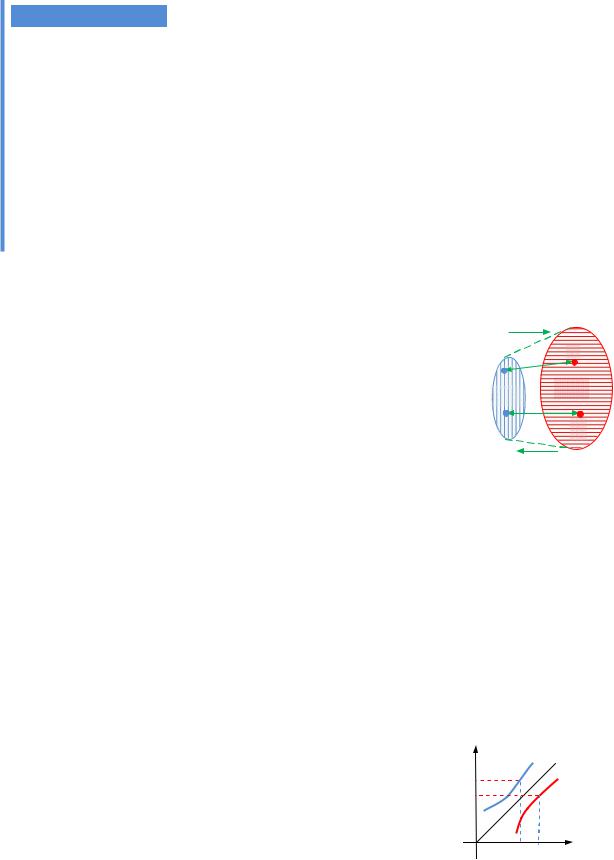
Геометрично обмеженість функції числом C означає, що її графік

розташований у смузі завширшки 2C.

f(x) M

m f (x)

f (x)

O a

b x

Рис. 2.14. Графік функції,

Рис. 2.15. Графік функції,

обмеженої зверху на

обмеженої знизу на

Рис. 2.16. Графік функції,

множині X

обмеженої на множині X

24	Розділ 1. Границя функції. Неперервність

Означення 2.6 (найменшого і найбільшого значень функції).

Точну верхню межу M значень неперервної на відрізку [a;b] функції називають найбільшим значенням функції на цьому відрізку і позначають

max f(x)	sup f(x) M.
[a;b]	x [a;b]

Точну нижню межу m значень неперервної на відрізку [a;b] функції f називають найменшим значенням функції на цьому відрізку і по-

значають
min f (x)	inf f (x) m.
[a;b]	x [a;b]

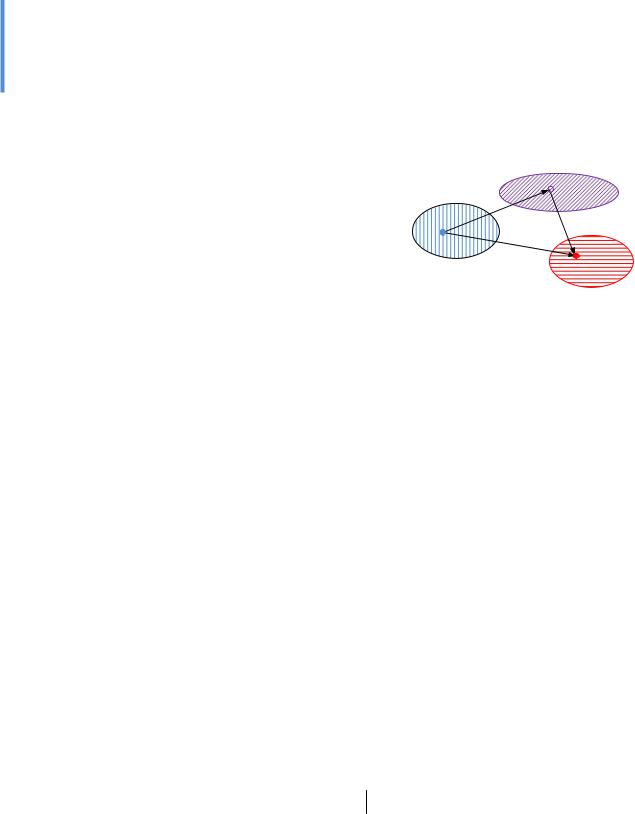
2.4. Обернена функція

Розгляньмо числову функцію

y f(x), x D(f ),

яка взаємно однозначно відображує множину D(f )

на множину E(f ).

Оскільки взаємно однозначна функція кожному елементу y E(f ) ставить у відповідність єдиний елемент x D(f ), то на множині E(f ) означено функцію

f
	y1
x1	E(f )
D(f )

x2 y2

f 1

Рис. 2.17. Взаємно обернені функції

f 1,

зобластю означення E(f ) і множиною значень D(f ), обернену до фун-

кції f . У цьому разі пишуть x (y) або x f 1(y). Отже, y f 1(x) : f (y) x.

Якщо функція обернена до функції f ,		то функція f буде оберне-
ною до функції . Про функції f	та кажуть, що вони взаємно обернені.
Функція y f (x) має обернену тоді й лише тоді, коли функція f
задає взаємно однозначну відповідність між множинами D та E.
Функцію y f (x) і обернену до неї функ-			y	y f(x) y x
цію x (y) зображує та сама крива. Графіки			y0
взаємно обернених функцій	y f (x)	та	x0	y f 1(x)

y (x) симетричні щодо прямої y x.			O	x0 y0 x
Функцію, до якої існує обернена функція,
			Рис. 2.18. Графіки взаємно
називають оборотною.			обернених функцій

	Лекція 2. Числові функції	25
	(достатня умова оборотності).	Якщо функція
Теорема 2.1	(достатня умова оборотності).	Якщо функція

y f (x) зростає (спадає) на множині X, то існує обернена до неї фу-

нкція x f 1(y), яка також зростає (спадає).

2.5. Складена функція

Нехай на множині D означено числову функцію u g(x) із множиною значень E

і на множині E задано функцію y f (u) із множиною значень F. Тоді функція g відображує елементи x D в елементи

u E, а функція f	відображує елементи
u E в елементи y	F :
g	f

D(f )

D(g) g(x) E g

D		f
x		f
x	f g	F
		F
		f(g(x))
		f(g(x))

Рис. 2.19. Схема відображень

для складеної функції y f (g(x))

x u y.

Кожному значенню x D зіставлено (з допомогою проміжної змінної u E) одне, цілком певне, значення y F.

У цьому разі y називають складеною функцією аргументу x і пишуть y f (g(x)), x D.

Складену функцію y f (g(x)) можна записати як ланцюжок рівностей:

yf (u), u g(x).

2.6.Елементарні функції

Тригонометричні функції

Нагадаймо, що тригонометричними функціями називають:

1)синус y sin x,D(f ) ;

2)косинус y cos x,D(f ) ;


	x			;
3) тангенс y tg x, D(f ) \ x			k,k
		2

4) котангенс y ctg x, D(f ) \ x x k,k .

26	Розділ 1. Границя функції. Неперервність

Обернені тригонометричні функції

Оберненими тригонометричними функціями називають:

1)арксинус y arcsin x,D(f ) [ 1;1];

2)арккосинус y arccos x,D(f ) [ 1;1];

3)арктангенс y arctg x,D(f ) ;

4)арккотангенс y arcctg x,D(f ) .

Гіперболічні функції

Гіперболічними функціями називають: 1) гіперболічний синус

	y sh x	ex e x	, D(f ) ;
2)		2
	гіперболічний косинус

	y ch x	ex e x	, D(f ) ;
3)		2
	гіперболічний тангенс

yth x chsh xx , D(f ) ;

4)гіперболічний котангенс

	y cth x ch x	, D(f ) \ {0}.
	sh x	y
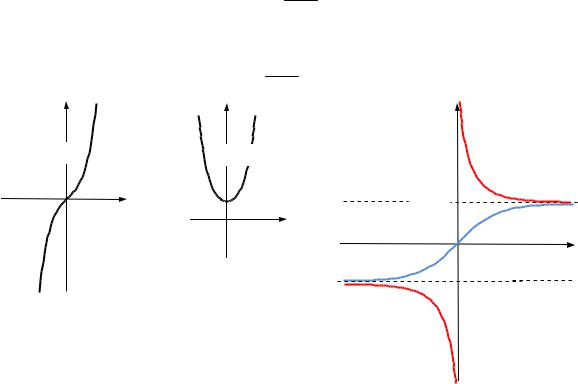
y	y	y
y sh x	y ch x	y cth x
		y cth x
O x	1	1
O x	1	y th x
	O x	O

	Рис. 2.21. Графік	1
Рис. 2.20. Графік	гіперболічного
Рис. 2.20. Графік	косинуса	y cth x
гіперболічного синуса

Рис. 2.22. Графіки гіперболічних тангенса і котангенса

Лекція 2. Числові функції

Співвідношення для гіперболічних функцій схожі на співвідно-

шення для тригонометричних функцій: 1) ch2 x sh2 x 1;

sh(x y) sh x ch y ch x sh y,


2)	y) ch x ch y sh x sh y;
ch(x	y) ch x ch y sh x sh y;


sh 2x 2 sh x ch x,


3)		2		2
	ch	2	x sh	2	x.
ch 2x	ch		x sh		x.

Основні елементарні функції

Основними елементарними функціями називають:

1)сталу функцію f (x) C, D(f ) ;

2)степеневу функцію y x , , D(f ) (0; );

3)показникову функцію y ax ,a 0,a 1, D(f ) ;

4)логарифмічну функцію y loga x,a 0,a 1, D(f ) (0; );

5)тригонометричні функції;

6)обернені тригонометричні функції.

Всі функції, одержані скінченною кількістю арифметичних дій над основними елементарними функціями, а також їхні суперпозиції,

утворюють клас елементарних функцій.

28	Розділ 1. Границя функції. Неперервність

ЛЕКЦІЯ 3. ГРАНИЦЯ ФУНКЦІЇ

3.1. Границя функції в точці

Точкою дотикання множини X називають точку x0, будь-який окіл якої містить точки множини X, відмінні від точки x0.

Приміром, точками дотикання інтервалу (a;b) будуть його внутрі-

шні точки і точки a та b. Єдиною точкою дотикання множини натуральних чисел є .

Розгляньмо функцію f (x), x X, і точку x0, яка є точкою дотикан-

ня множини X.

(границі функції мовою околів, за Коші). Точку A

Означення 3.1

називають границею функції f (x), x X,

у точці x0,

якщо для будь-

якого -околу U (A) точки A існує проколений -окіл U (x0 ) \ {x0 } точки

x0, такий, що для всіх

x X U (x0 ) \ {x0 }

відповідні значення функції

f (x) U (A)

і позначають

lim f (x) A.

x x0

Розпишімо окремі випадки сформульованого означення.

1. x0, A — числа. Число A назива-

y f(x)

ють границею функції f (x), x X,

у точ-

(A)

ці x0, якщо для будь-якого 0

існує

таке 0, що з нерівності

U (x0 )

x x0

O x0

x0 x

випливає нерівність

Рис. 3.1. Скінченна границя

f(x) A

функції

f(x) коли x x0

Або

lim f(x) A 0 ( ) 0 x X :

x x0

0 x x0 f(x) A .

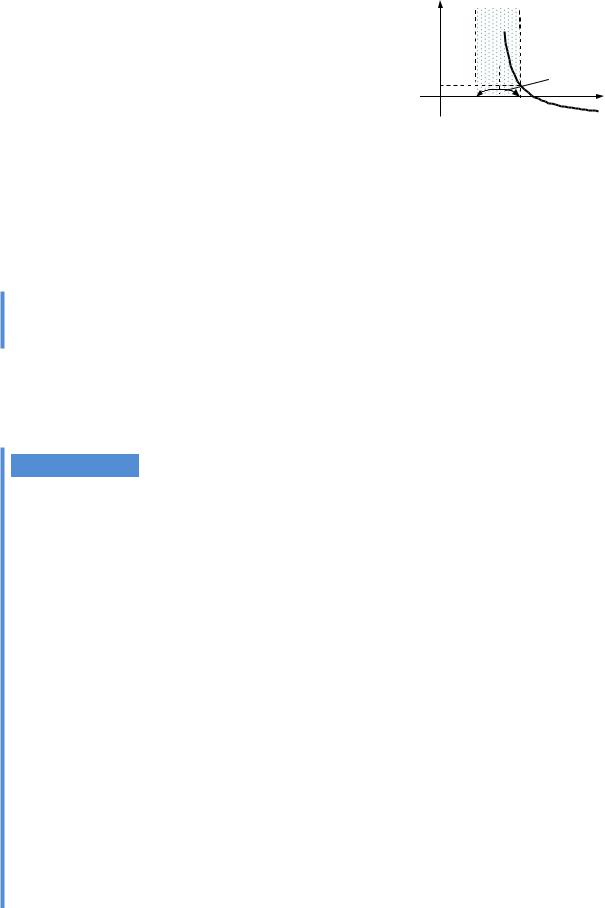
Лекція 3. Границя функції

2. x0 — число, A .

lim f(x) 0 ( ) 0 x X :

x x0

f(x)

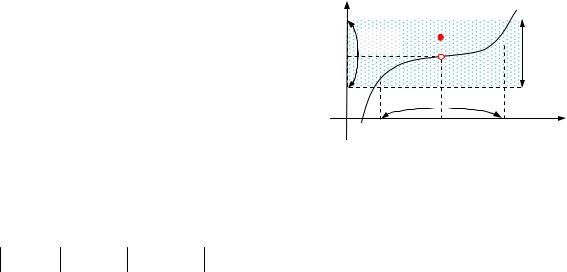
Якщо lim f (x) , то графік функ-

x x0

ції має в точці x0 вертикальну асимптоту x x0.

y f(x)

		U(x0 )
	x0
O	x0	x

Рис. 3.2. Нескінченна границя функції f(x), коли x x0

(за Коші)

3. A f (x0). Якщо функція f (x), x X, означена в точці x0 X ра-

зом з деяким її околом і lim f(x) f(x0), то функцію f (x) називають

x x0

неперервною в точці x0.

Будь-яка елементарна функція неперервна в кожній точці своєї області означення.

Точка x0 може як належати області означення функції f так і не нале-

жати. Оскільки під час знаходження границі точку x0 виключають з ро-

згляду, то існування границі функції в точці є локальною властивістю функції.

Теорема 3.1 (про функції, що мають скінченну границю).

1 (єдиність границі). Якщо функція f має скінченну границю в точці x0, то ця границя єдина.

2 (обмеженість). Якщо f має скінченну границю в точці x0, то існує проколений окіл точки x0, у якому функція f обмежена.

3 (збереження знаку). Якщо функція f має скінченну додатну (від’ємну) границю A в точці x0, то існує проколений окіл точки x0, в

якому функція f додатна (від’ємна).

4 (збереження нерівності). Якщо в деякому проколеному околі точки

x0	правдива нерівність f1(x) f2(x) і існують скінченні границі
lim f1(x), lim f2(x), то
x x0	x x0
	lim f1(x) lim f2(x).
	x x0	x x0

5 (теорема про проміжну функцію, про «двох вартових»). Якщо

lim f1(x)	lim f2(x) A і в деякому проколеному околі точки x0
x x0	x x0
правдиві нерівності f1(x) f (x) f2(x), то		lim f(x) A.
		x x0

30	Розділ 1. Границя функції. Неперервність

3.2. Границя числової послідовності

Розгляньмо важливий випадок скінченної границі A функції f(x) у точці x0 :

lim f(x) A 0 ( ) 0 x X :

x f(x) A .

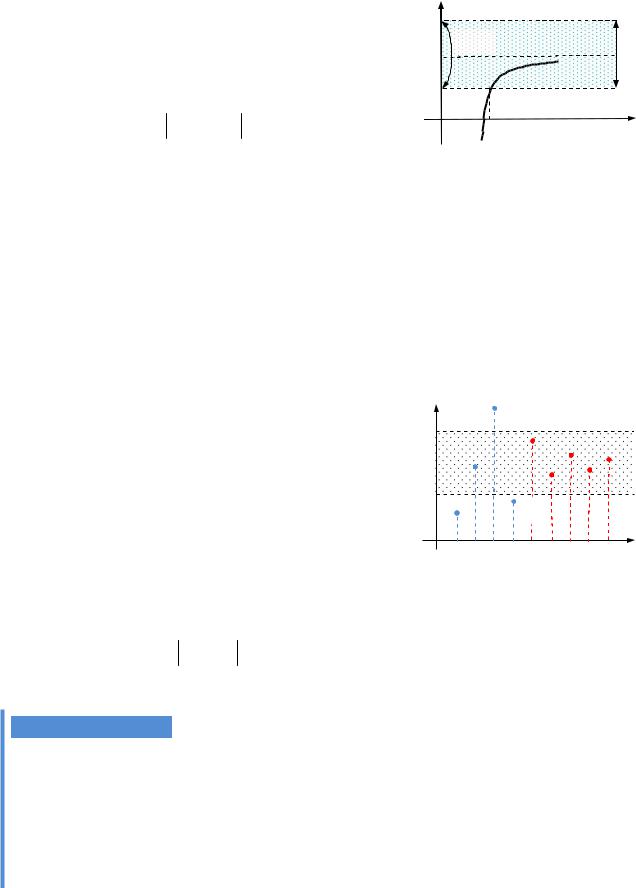
Якщо lim f (x) A, то графік функції

має горизонтальну асимптоту y A.

A	U (A)	2

		y f(x)

Рис. 3.3. Скінченна границя функції f(x) коли x

Оскільки єдиною точкою дотикання множини натуральних чиселє , то границю послідовності можна розглядати, коли n .

			(границі послідовності). Точку a		називають гра-
		Означення 3.2	(границі послідовності). Точку a		називають гра-
		ницею послідовності {xn}, якщо для будь-якого додатного числа
	знайдеться номер N N( ) такий, що всі члени послідовності з но-
	мерами n N потраплять в -окіл точки a і пишуть
			lim xn a або xn a, коли n .
			n
		Числову послідовність, що має скін-		xn
		Числову послідовність, що має скін-		xn
ченну границю a, називають збіжною до				a
числа a і розбіжною, якщо вона не має				a
числа a і розбіжною, якщо вона не має				a
скінченної границі.				a
		Послідовність {xn } збігається до чи-		a
сла a, якщо поза межами будь-якої симе-
тричної горизонтальної смуги завширш-				O 1 2 3	4 5 6 7 8 9 n
ки 2 міститься лише скінченна кіль-					N
кість точок послідовності.				Рис. 3.4. Геометричний зміст
		lim xn a 0 N :		збіжної послідовності
		n

n N xn a .

Границя послідовності не залежить від відкидання скінченної кількості членів послідовності або їх змінювання.

Означення 3.3 (границі функції мовою послідовностей, за

Гейне). Точку A називають границею функції f (x), x X,				у то-
чці x0	,	якщо для будь-якої послідовності точок {xn},	збіжної до
x0 (xn	x0 )	відповідна послідовність значень функції {f	(xn )}	збіга-

ється до точки A, тобто
lim xn x0	lim f(xn ) A.
n	n

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.08.201958.88 Кб2kol2 вопросы 1-10.doc
#
29.04.20194.18 Mб19kolomijchuk_shema.doc
#
17.03.20165.82 Mб48KOMPAS_METODA13_2.pdf
#
17.03.201621.24 Mб91KOMPAS_ЗАВДАННЯ2013_8.pdf
#
17.03.20164.55 Mб49konspect_lectsiy-ln_lm.pdf
#
12.05.20152.01 Mб15Konspekt lek. MA-1.pdf
#
17.03.20163.92 Mб456konspekt_lekcii_ek_pp_um_uk_novii_dlya_stud_2.docx
#
17.03.20163.26 Mб45konspekt_lektsy_Ch1.doc
#
19.09.20193.12 Mб74Konspekt_modelirovanie2.doc
#
18.09.2019547.84 Кб1Konspekt_Skor_Fil.doc
#
12.05.201521.5 Кб10Kontrollarbeit # 3.docx