Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Konspekt lek. MA-1

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

2.01 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1110 11 > Следующая >>>


Лекція 15. Інтегрування раціональних функцій										91
		P (x)		a xn a		xn 1	... a	0
R(x)		n		n	n 1			0	.
R(x)									.
	Qm (x)		bmxm bm 1xm 1				... b0

Якщо степінь многочлена в чисельнику менше за степінь многочлена у знаменнику (n m), то дріб називають правильним. Якщо степінь многочлена у знаменнику не перевищує степеня многочлена у знаменнику (n m), то дріб називають неправильним.

Будь-який неправильний раціональний дріб можна зобразити як суму многочлена (цілої частини) і правильного раціонального дробу:

Pn (x)

Rn m (x)

P(x)

Qm (x)

Pn (x)

де Rn m(x)

— ціла частина дробу

;P(x) — остача від ділення

Qm (x)

Pn (x) на Qm(x).

15.2. Інтегрування елементарних раціональних дробів

Елементарним дробом називають правильний раціональний дріб одного з чотирьох типів:

1) x A a ;

2) (x a)n (n 2);

Mx N 3) x2 px q ;

Mx N

4) (x 2 px q)n (n 2).

Тут A,a, p,q, M, N — дійсні числа, а квадратний тричлен не має дійсних коренів, тобто p2 4q 0.

Елементарні дроби 1-го та 2-го типів інтегрують безпосередньо з допомогою основних правил інтегрального числення:

Adx

d(x a)

A ln

x a

92	Розділ 3. Інтегральне числення функцій однієї змінної

2.	Adx	A (x a) nd(x a)	A		C.
	n			n 1
	(x a)		(1 n)(x a)

Інтеграл від елементарного дробу 3-го типу зводиться до табличних інтегралів вилученням у чисельнику диференціала знаменника. А саме,

(Mx N )dx

d(x2 px q) (2x p)dx

Mx N

(2x p) N

x2 px q

d x

d(x

x px

2x p

ln(x

px q)

arctg

4q p

2 4q

4. Інтеграл

Mx N

px q)

заміною

t x p2

зводиться до інтеграла

In (t2 a2 )n ,

який можна знайти за рекурентною формулою

	1						t
	1						t
In

			2	(2n 3)In 1		2	2	n 1	,n 2, 3,...
	2(n	1)a	2		(t	2	2	n 1
	2(n	1)a			(t		a	)

Приміром, знаючи табличний інтеграл

I1			dt		1	arctg	t	C,
	t	2	a	2	a
						a

за рекурентною формулою знаходимо, що

arctg

) 2a

Лекція 15. Інтегрування раціональних функцій

15.3. Інтегрування раціональних дробів

Розкладання раціонального дробу на суму елементарних дробів

Теорема 15.1 (про розклад на суму елементарних дробів).

Правильний дріб

Pn (x)

(n m)

зі знаменником

Q (x)

(x) a

(x a ) 1 (x a

) 2 ...(x a

) k

(x2 p x q

) 1 ...(x

2 p x q

) l ,

,i 1,k, j

, p2j

4qj

0, j 1,l,

можна єдиним чином розкласти на суму елементарних дробів:

P (x)

...

Qm(x)

x a1

a1)2

(x a1) 1

...

k 2

...

(x ak )2

(x ak ) k

M x N

M1 x N1

...

2 p x q

(x2

p x q

) 1

x N

Ml x Nl

...

2 p x

(x2 p x q

) l

У цьому розкладі

A11,..., A1 1 ,..., Ak1,...,Ak k ,

M11, N11,..., M1 1 , N1 1 ,..., Ml1, Nl1,...,Ml l , Nl l

— деякі дійсні сталі, невизначені коефіцієнти, частина яких може дорівнювати нулеві. Їхня загальна кількість дорівнює степеню многочлена у знаменнику, тобто m.

Приміром,

x	A	Bx C	.
(x 2)(x2 2x 4)	x 2
		x2 2x 4

Невизначений інтеграл від будь-якої раціональної функції завжди виражається через скінченну кількість елементарних функцій.

94	Розділ 3. Інтегральне числення функцій однієї змінної

Метод невизначених коефіцієнтів

1. Спосіб прирівнювання коефіцієнтів.

Щоб знайти невизначені коефіцієнти розкладу, праву частину рівності зводять до спільного знаменника і прирівнюють коефіцієнти при однакових степенях x у чисельниках лівої та правої частин. Тобто одержують систему лінійних рівнянь, із яких і знаходять невизначені коефіцієнти.

Приміром, знайдімо коефіцієнти розкладу:

x	A	Bx C	,
(x 2)(x2 2x 4)	x 2	x2 2x 4

Праву частину цього розкладу зведімо до спільного знаменника:.

x		A(x2 2x 4) (Bx C )(x 2)
(x 2)(x2		x3	8
	2x 4)

x (A B)x2 (2A C 2B)x 4A 2C.

Прирівнюючи коефіцієнти при однакових степенях x, одержуємо систему лінійних алгебричних рівнянь:

	2
	2
x		0 A B
x		0 A B
	1			1		1		1
	1			1		1		1
x		1 2A C 2B	A		,B		,C		.
x		1 2A C 2B	A		,B		,C		.
	0			6		6		3
x	0	0 4A 2C		6		6		3
x		0 4A 2C

2. Спосіб домноження (викреслювання). Нехай

	Pn(x)			Pn (x)		,	(a) 0.
Qm(x)				(x a) (x)

Кратному дійсному кореню x a відповідає в розкладі дробу

Pn(x) низка елементарних дробів:

Qm (x)

A	A 1	...	A1	.
(x a)	(x a) 1		x a

Коефіцієнт A знаходять за формулою

A	Pn(x)		Pn(a)	,


	(x a) (x)		(a)
		x a

а решту коефіцієнтів за формулами:

				(k )
				(k )
	1	P (x)
		n
A					,k 1, 1.
k
	k !
		(x a)	(x)		x a
					x a

Лекція 16. Інтегрування тригонометричних виразів

ЛЕКЦІЯ 16. ІНТЕГРУВАННЯ ТРИГОНОМЕТРИЧНИХ ВИРАЗІВ

16.1. Інтеграл вигляду R(sin x, cos x)dx

Загальний підхід

Умовимося через R(u,v,w,...) позначати раціональну функцію щодо u,v,w,..., тобто вираз, який одержано з величин u,v,w,..., а також дійсних чисел з допомогою чотирьох арифметичних дій.

Розгляньмо нетабличний інтеграл вигляду

R(sin x, cosx)dx,

де підінтегральна функція є раціональною функцією від sin x та cos x. Знайти його можна різними методами. Іноді буває досить перетворити підінтегральний вираз, використовуючи відомі тригонометричні формули, застосувати методи підведення множника під знак диференціала, заміни змінної або інтегрування частинами.

Універсальна тригонометрична підстановка

Для обчислення інтегралів вигляду R(sin x, cos x)dx існує загальна

універсальна схема обчислення, яка ґрунтується на універсальній тригонометричній підстановці

t tg x2 , x ( ; ).

Цим підставленням інтеграл R(sin x, cos x)dx перетворюють в інтег-

рал від раціональної функції змінної t, який завжди виражається в елементарних функціях.

Справді, нехай t tg

. Виразімо sin x, cos x

та dx через t :

sin x

cos x

1 t2

x 2 arctg t,

2dt

Тоді

1 t

2dt

R(sin x, cos x)dx

R1(t)dt.

96	Розділ 3. Інтегральне числення функцій однієї змінної

За допомогою універсальної підстановки зручно обчислювати інтеграли вигляду

a cos x b sin x c.

Універсальна підстановка інколи приводить до порівняно громіздких раціональних дробів. Тому буває зручнішим використовувати інші підстановки.

1) якщо підінтегральна функція непарна щодо sin x, тобто

R( sin x, cos x) R(sin x, cos x),

то застосовують підстановку

cos x t, x [0; ];

2) якщо підінтегральна функція непарна щодо cos x, тобто

R(sin x, cos x) R(sin x, cos x),

то застосовують підстановку

		;	;
sin x t, x
	2	2

3) якщо підінтегральна функція парна щодо sin x та cos x, тобто

R( sin x, cos x) R(sin x, cos x),

то застосовують підстановку


		;
tg x t, x		;	.
	2
	2		2

Інтеграли вигляду sinn x cosm xdx

1. Якщо хоча б одне з чисел m або n — непарне, то відокремлюють від непарного степеня один співмножник і виражають із допомогою формули sin2 x cos2 x 1 парний степінь, що залишився. Отже,

1) якщо m 2k 1,k , то підінтегральний вираз перетворюють

так:

sin2k 1 xdx sin x(sin x)2k 2dx (1 cos2 x)k 1d(cos x);

2) якщо n 2k 1,k , то підінтегральний вираз перетворюють

так:

cos2k 1 xdx (1 sin2 x)k 1d(sin x).

2. Якщо ж m та n — парні числа, то степені понижують, переходячи до подвійного аргументу за допомогою формул:

Лекція 16. Інтегрування тригонометричних виразів

cos2 x

1 cos 2x , sin2 x

1 cos 2x ,

sin x cos x

1 sin 2x.

Отже,

cos 2x

sin

x cos

,k,l

16.2. Інтеграли вигляду tgn xdx, ctgnxdx

Для знаходження інтегралів цього типу використовують тригонометричні тотожності:

tg2 x

cos

ctg2 x

а саме:

sin2 x

n 2

x tg

1 ;

cos

n 2

ctg

x ctg

1 .

sin

16.3. Інтеграли від добутку тригонометричних функцій

Інтеграли вигляду

sin mx cosnxdx, cosmx cosnxdx, sin mx sin nxdx (m,n ).

Їх обчислюють розкладанням підінтегральної функції в суму за формулами:

sin mx cosnx 12 (sin(m n)x sin(m n)x), cos mx cosnx 12 (cos(m n)x cos(m n)x), sin mx sin nx 12 (cos(m n)x cos(m n)x).

98	Розділ 3. Інтегральне числення функцій однієї змінної

ЛЕКЦІЯ 17. ІНТЕГРУВАННЯ ІРРАЦІОНАЛЬНИХ ВИРАЗІВ

17.1. Дробово-лінійна підстановка

Інтеграли вигляду

, ...,

R x,

Тут m1, n1, ..., mk , nk , R( )

— раціональна функція. Такі інтеграли

зводять до інтегралів від раціональних функцій заміною

x ts,

де s — найменший спільний знаменник дробів

, ...,

ax b

, ...,

Інтеграли вигляду

R x,

Тут m1, n1, ..., mk , nk . Ці інтеграли зводять до інтегралів від раціо-

нальної функції заміною

ax b ts , cx d

де s — найменший спільний знаменник дробів m1 , ..., mk . n1 nk

Інтеграли від ірраціональних функцій не завжди виражаються через елементарні функції. Приміром, еліптичні інтеграли 1-го та 2-го роду

	dx				,	x2dx				,

(1	2	)(1	2 2	)		2	)(1	2 2
(1	x	)(1	k x	)		(1 x	)(1	k x	)

0 k 1,

не інтегруються в елементарних функціях.

	Лекція 17. Інтегрування ірраціональних виразів					99
17.2. Інтеграли вигляду R(x,					)dx
17.2. Інтеграли вигляду R(x,				ax2 bx c	)dx
1. Інтеграл		Mx N	dx обчислюють вилученням у чисель-


		ax2 bx c
		ax2 bx c

нику диференціала від підкореневого виразу і, при потребі, вилучен-

ням повного квадрату під коренем.

Приміром,

3x 1

d(x2 2x 2) (2x 2)dx

3x 1

3 (2x 2) 4

x2 2x 2

(2x

dx 3

(2x 2)dx

x2 2x 2

d(x2

2x 2)

d(x 1

x2 2x 2

(x 1)2 1

4 ln x 1 (x 1)2 1

x2 2x 2

2. Інтеграл вигляду

зводять до попередньо-

(x ) ax2 bx c

го типу заміною

x 1t .

3.Тригонометричні підстановки. Інтеграли вигляду

R(x, k2 x2 )dx, R(x, 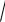x2 k2 )dx

можна зводити до раціональних функцій підстановками:

1)											, для інтеграла R(x,
																	2		2
	x k sin t, t						;									k	2	x	2		)dx;
	x k sin t, t				2		;		2							k		x			)dx;
					2				2


																	2			2
2)						;						для інтеграла R(x,				x	2	k		2		)dx;
2)	x k tg t, t					;				,		для інтеграла R(x,				x		k				)dx;
					2
					2				2

		k
		k													2			2
3)	x									для інтеграла					2			2
								,					R(x,	x		k )dx.
			, t 0;					,					R(x,	x		k )dx.
		cos t		2

Тригонометричні підстановки найефективніші в обчисленні визначених інтегралів, де не потрібно вертатись до старої змінної.

100	Розділ 3. Інтегральне числення функцій однієї змінної

4. Інтеграли 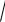x2 a2dx, 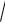a2 x2dx можна також знаходити

інтегруванням частинами.

17.3. Інтегрування диференціального біному

Теорема 17.1 (Чебишова). Інтеграли вигляду

xm(a bxn )pdx (m, n, p ,a,b )

від диференціального біному виражаються через елементарні функції лише у трьох випадках:

1) якщо p , то застосовують підстановку x ts , де s — найменший спільний знаменник дробів m та n;

2) якщо	m 1	,	то застосовують підстановку a bxn
	n

знаменник дробу p s ;

3) якщо m 1 p , то застосовують підстановку ax n n

— знаменник дробу p s .

ts , де s —

b ts , де s

У решті випадків інтеграли від диференціального біному не виражаються через елементарні функції.

Приміром,

3	1 4
3	1 4		x			1 2			1 4 1 3
				dx x			(1	x		)	dx

		x
		x
							m			1 , n		1 , p	1	;
							m			1 , n		1 , p	1	;
					m 1					2		4	3
					m 1	2 1 x1 4 t3;t (1 x1 4)1 3;
					n			1 x 3 4dx 3t2dt
								1 x 3 4dx 3t2dt
								4

x1 4(1 x1 4 )1 3x 3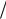4dx (t3 1)t 12t2dt 12 (t6 t3)dt

	t	7	t	4		12 3
		7		4
							4 7 3	4 4
					C		(1 x ) 3 (1 x )		C.

12	7		4			7
	7		4			7

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1110 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.08.201958.88 Кб2kol2 вопросы 1-10.doc
#
29.04.20194.18 Mб16kolomijchuk_shema.doc
#
17.03.20165.82 Mб47KOMPAS_METODA13_2.pdf
#
17.03.201621.24 Mб88KOMPAS_ЗАВДАННЯ2013_8.pdf
#
17.03.20164.55 Mб39konspect_lectsiy-ln_lm.pdf
#
12.05.20152.01 Mб13Konspekt lek. MA-1.pdf
#
17.03.20163.92 Mб446konspekt_lekcii_ek_pp_um_uk_novii_dlya_stud_2.docx
#
17.03.20163.26 Mб39konspekt_lektsy_Ch1.doc
#
19.09.20193.12 Mб59Konspekt_modelirovanie2.doc
#
18.09.2019547.84 Кб1Konspekt_Skor_Fil.doc
#
12.05.201521.5 Кб10Kontrollarbeit # 3.docx