
ТЕМА 5. Кінетостат. аналіз мех
..pdf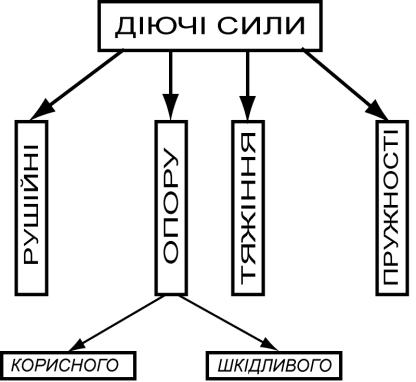
ТЕМА 5. КІНЕТОСТАТИЧНИЙ АНАЛІЗ МЕХАНІЗМІВ
5.1. Задачі
Визначення реакцій (тисків) у кінематичних парах механізму
з урахуванням сил інерції, а також зрівноважувальної сили або
зрівноважувального моменту, які прикладені до початкової ланки.
При цьому аналізі відомі:
кінематична схема механізму (КСМ);
масові характеристики ланок (маси, моменти інерції, положення центрів мас);
зовнішні сили, що діють на ланки механізму;
закон руху початкової ланки.
5.2. Сили, що діють на ланки механізму
Розглянемо блок-схему, наведену на рис. 5.1.
Рис. 5.1. Сили, що діють на ланки механізму
57
5.2.1. Рушійні сили – це сили, робота яких за цикл усталеного руху додатна.
dA F ds cos[ |
F |
, |
ds |
]. |
(5.1) |
Рушійні сили задаються у вигляді |
діаграм, наприклад |
||||
(рис. 5.2): |
|
||||
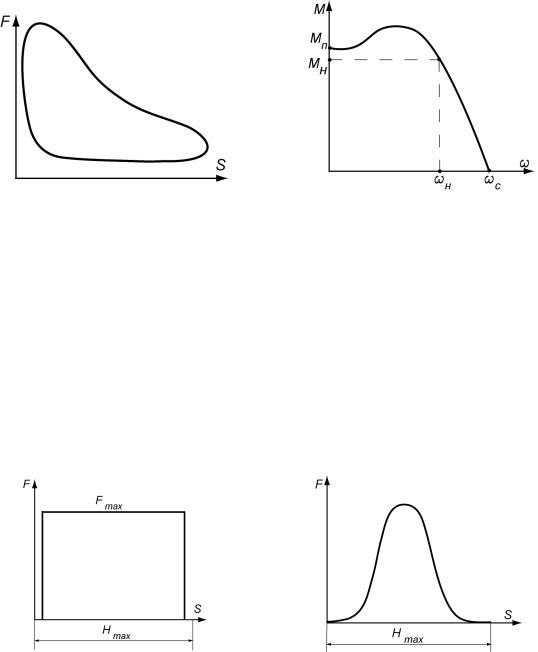
а. б.
Рис. 5.2:
а. – індикаторна діаграма для ДВЗ; б. – механічна характеристика асинхронного двигуна
5.2.2. Сили опору – це сили, робота яких за цикл усталеного руху від'ємна.
5.2.2.1. Сили корисного опору – це сили, для подолання яких призначено механізм.
Сили корисного опору задаються у вигляді діаграм, наприклад, (рис. 5.3):
а. б.
Рис. 5.3:
а. – сила різання в металообробних верстатах; б. – сила тиску в пресах
58
5.2.2.2. Сили шкідливого опору – це сили, для подолання яких необхідно витратити роботу понад тої роботи, що йде на виконання технологічного процесу. Наприклад, сили тертя в кінематичних парах механізму.
5.2.3. Сили тяжіння
G m g, |
(5.2) |
де m - маса, кг; g - прискорення вільного падіння, м/с2.
Робота сил тяжіння за цикл усталеного руху дорівнює нулю.
5.2.4. Сили пружності
Fпруж c x, |
(5.3) |
де c - коефіцієнт жорсткості, Н/м; x - переміщення, м.
Робота сил пружності за цикл усталеного руху дорівнює
нулю.
5.3. Принцип кінетостатики
Принцип кінетостатики полягає в тому, що в число зовнішніх сил, що діють на ланки механізму, запроваджують сили інерції, які є фіктивними для самої ланки, але реальними для її зв'язків.
Принцип кінетостатики ґрунтується на відомому положенні Д'Аламбера, згідно з яким система сил, до якої уведені сили інерції, вважається рівноважною, і для неї придатні рівняння статики.
Отже, при включенні в число сил, що діють на ланку, сили інерції, ланка умовно вважається у стані спокою, тому можна застосовувати рівняння статики. Цей принцип є методологічним.
5.4.Урахування сил інерції
5.4.1.Плоскопаралельний рух ланки
Згадаємо спочатку поняття маси і моменту інерції. Маса – це міра інертності тіла при поступальному русі. Момент інерції – це аналог маси при обертальному русі. Зв'язок між масою і моментом інерції:
IS m S2 , |
(5.4) |
де m - маса, кг; S - радіус інерції, м.
59
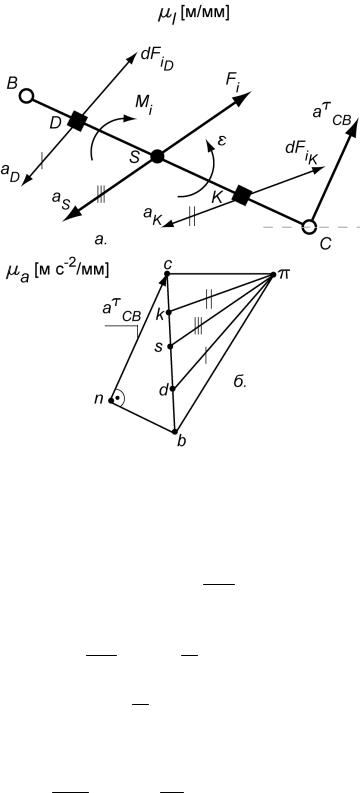
Розглянемо ланку ВС, яка здійснює плоскопаралельний рух (рис. 5.4,а) та її план прискорень (рис. 5.4,б).
Рис. 5.4. Урахування сили інерції при плоскопаралельному русі ланки:
а. – ланка, що здійснює плоскопаралельний рух; б. – план прискорень ланки
Елементарна сила інерції dFіi для матеріальної точки визначається за формулою:
dFі dmi ai , |
(5.5) |
i |
|
де dmi - елементарна маса; ai - прискорення матеріальної точки. Виділяємо на ланці ВС (рис. 5.4, а) матеріальну точку D, тоді
для неї:
dFiD dmD aD dmD d a .
60

Аналогічно для матеріальної точки К:
dFiK dmK aK dmK k a .
Але ланка – це система матеріальних точок, отже, для ланки маємо головний вектор сил інерції, Н:
|
|
|
|
|
Fi m aS m s a , |
(5.6) |
|||
де m - маса ланки, кг; aS s a - прискорення центра мас ланки, м/с2.
Ураховується також головний момент сил інерції, Нм:
Mi IS |
, |
(5.7) |
де IS - момент інерції, кгм2; - кутове прискорення ланки, с-2.
|
aCB |
|
nc a |
, |
(5.8) |
lCB |
CB l |
де aCB - тангенціальне прискорення, м/с2; lCB - довжина ланки, м.
Для спрощення розрахунків головний вектор Fi і головний
момент Mi сил |
інерції |
замінюються результуючою силою Fi , |
|||||||||||
плече якої h дорівнює (рис. 5.5): |
|
|
|
|
|
|
|||||||
h |
Mi |
|
|
IS |
|
або в масштабі: z |
i |
|
hi |
. |
(5.9) |
||
|
|
|
|
||||||||||
i |
F |
|
m a |
S |
|
|
|
l |
|||||
|
i |
|
|
|
|
|
|
|
|||||
Рис. 5.5. Прикладання результуючої сили інерції
61
Із центра мас ланки S проводимо коло радіусом zi ,
результуюча сила Fi прикладається по дотичній до цього кола,
паралельно та протилежно ( s), і утворює момент проти
(рис. 5.5).
5.4.2. Поступальний рух ланки
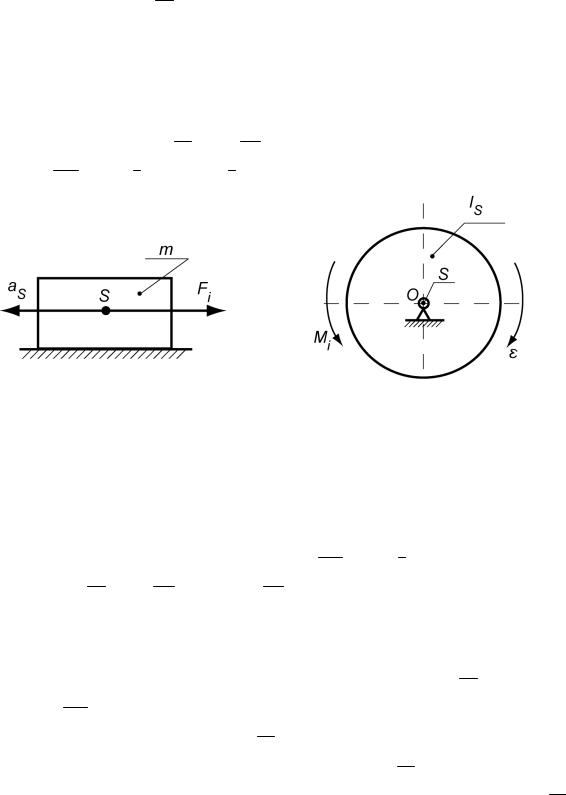
При поступальному русі ланки враховується тільки головний вектор сил інерції Fi m aS m s a , а головний момент сил інерції Mi IS 0, т. щ. 0 (рис. 5.6).
Рис. 5.6. Урахування сил |
Рис. 5.7. Урахування сил інерції |
інерції при поступальному |
при обертальному русі навколо |
русі ланки |
центральної осі |
5.4.3. Обертальний рух ланки навколо центральної осі
При обертальному русі навколо центральної осі враховується тільки головний момент сил інерції Mi IS , а головний вектор сил інерції Fi m aS 0, т. щ. aS 0 (рис. 5.7).
5.4.4. Обертальний рух відносно довільної осі
До ланки ОА прикладені головний вектор Fi і головний момент Mi сил інерції (рис. 5.8).
Переносимо вектор Fi у довільну точку K, одразу
прикладаючи протилежно йому той же вектор Fi .
Визначаємо плече h (це перпендикуляр із т. K на вектор Fi ):
h |
Mi |
|
IS |
|
m aS |
||
|
Fi |
||
62
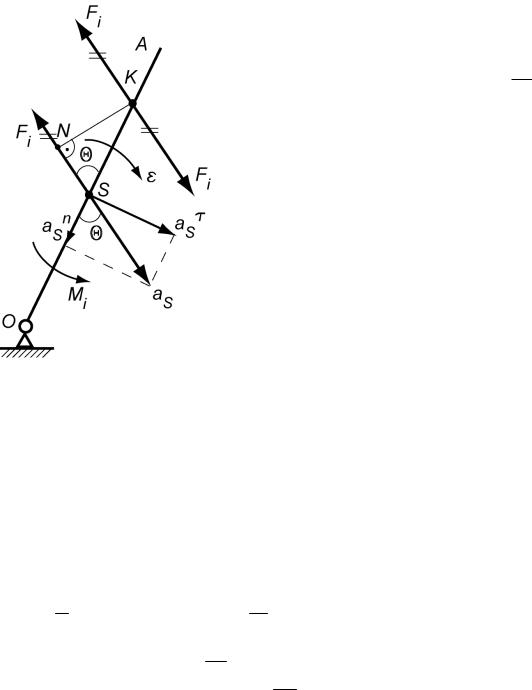
Рис. 5.8. Урахування сил інерції при обертальному русі відносно довільної осі
Визначаємо відстань SK, розглядаючи трикутник KSN:
lSK |
|
|
h |
|
|
|
|
IS |
|
|
|
||||||
sin |
|
m aS |
sin |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
aS |
|
|
|
|
||
|
|
m S2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
a |
|
|
|
m 2 |
|
|
|
2 |
||||||
|
|
I |
S |
|
|
|
|
|
|||||||||
|
|
|
S |
|
|
|
S |
|
|
|
S |
||||||
m aS lOS |
|
mlOS |
lOS |
||||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Отже, |
lSK |
|
|
S |
, |
|
|
|
|||||||
|
|
lOS |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
де S - радіус інерції, м.
aS
lOS
IS |
|
|
m aS |
||
|
.
(5.10)
Точка K називається центром хитання ланки.
5.5. Умови статичної визначуваності кінематичного ланцюга
(КЛ)
5.5.1. Кінематичний ланцюг із нижчими парами
Нехай до ланки ВС із нижчими парами прикладені головний
вектор F і головний момент M усіх сил, ураховуючи й сили інерції
(рис. 5.9).
Невідомими є: Fli - реакція в шарнірі В (невідома
за величиною та напрямком); Fki - реакція у поступальній парі (невідома за величиною та точкою прикладання).
Позначимо: n – число рухомих ланок КЛ; 3n – число рівнянь, які можна скласти; p5 – число кінематичних пар (КП) 5-го класу; 2p5 - число невідомих реакцій.
Перевіряємо умову статичної визначуваності для ланки: замість умови 3n 2p5 маємо 3 1 2 2 або 3 4.
63

|
Висновок: |
|
|
|
|
|
У кінематичному ланцюгу |
||||
|
з нижчими |
парами |
ланка |
||
|
з прикладеними |
до |
неї силами |
||
|
є статично |
невизначеною |
|||
|
системою. |
|
|
|
|
|
Отже, |
і |
механізм |
||
|
із нижчими парами є статично |
||||
|
невизначеною системою. |
|
|||
|
Перевіряємо |
|
умову |
||
|
статичної |
визначуваності |
для |
||
|
групи Ассура: |
|
|
|
|
Рис. 5.9. Ланка з нижчими парами |
W 3n 2p5 |
0 |
|
(5.11) |
|
або 3n 2p5 - умова статичної визначуваності групи Ассура.
Висновок: для визначення реакцій у кінематичних парах механізму його треба розділити на групи Ассура і для цих груп обчислювати невідомі реакції.
5.5.2. Кінематичний ланцюг із вищими парами
Нехай до ланки ВС із вищою парою С прикладені головний
вектор F і головний момент M усіх сил, ураховуючи й сили інерції
(рис. 5.10).
Невідомими є: Fli - реакція в шарнірі В (невідома за
величиною та напрямком); Fki - реакція в поступальній парі (невідома за величиною), точка прикладання її відома.
Умова |
|
|
статичної |
визначуваності |
плоского КЛ |
||
із вищими парами: |
|
||
W 3n 2p5 |
p4 0 або |
||
3n 2p5 |
p4 , |
(5.12) |
|
отже, 3 1 2 1 1 1, 3=3. |
|||
Умова |
|
справедлива |
|
тільки для |
плоскої |
системи |
|
Рис. 5.10. Ланка з вищою парою сил.
64

5.5.3. Умова статичної визначуваності просторового кінематичного ланцюга (КЛ)
Для просторового КЛ справедлива умова:
W 6n 5p5 4p4 3p3 2p2 p1 0 або
6n 5p5 4 p4 3p3 |
2p2 p1 . |
(5.13) |
|
5.6. Силовий розрахунок груп Ассура |
|
||
Силовий розрахунок |
проведемо |
на прикладі вже |
відомого |
з КАМ шарнірно-важільного |
механізму |
завантажника, наведеного |
|
на рис. 4.4. Силовий розрахунок проводимо для одного заданого робочого положення механізму (рис. 5.11).
Механізм є статично невизначеною системою, тому розділяємо його на групи Ассура 4-5 (рис. 5.11, в), 2-3 (рис. 5.11, д) і початкову ланку (рис. 5.11, ж).
Розрахунок здійснюється за формулою будови механізму, починаючи з останньої приєднаної групи Ассура:
I 0,1 II2 2,3 II2 4,5 .
5.6.1.Група 4-5 (рис. 5.11, в)
1.Визначаємо сили, що діють на групу 4-5:
сили тяжіння, Н:
G5 m5 g; |
G4 m4 g , |
де m4 ,m5 - маси ланок 4 і 5, |
кг (за завданням); g 10м/с2 - |
прискорення вільного падіння. Сили тяжіння прикладені в центрах мас S4 ,S5 .
сила корисного опору FКО , Н, визначається для даного положення механізму за заданим графіком FКО FКО S , вона прикладена в т. С повзуна (напрямок за завданням або проти
вектора швидкості повзуна pc5 ).
сили інерції ланок, Н:
повзуна С:
|
|
|
|
m5 s5 a m5 c5 a , |
|
Fi m5 aS |
5 |
(5.14) |
|||
5 |
|
|
|
|
|
65

де aS5 =aC5 , т. щ. точки S5 і C5 збігаються. Прикладена в т. С
повзуна проти вектора прискорення c5 .
шатуна СВ:
Fi4 m4 aS4 m4 s4 a - головний вектор сил інерції;
|
|
M i4 IS4 4 |
|
- головний момент сил інерції, Нм; |
|
|
||||||||||||||||||||||||||||||||||||
де IS4 |
- |
|
момент |
|
|
інерції, |
кгм2 |
(за |
|
завданням); |
|
|
|
|
|
- |
кутове |
|||||||||||||||||||||||||
|
|
|
|
|
|
4 |
||||||||||||||||||||||||||||||||||||
прискорення ланки, с-2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aC |
B |
n |
3 |
c |
4 |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
4 |
4 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
(5.15) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BC l |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lCB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Плече результуючої сили інерції, м: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
h |
4 |
|
Mi |
4 |
або в масштабі |
l |
, мм: |
z |
4 |
|
h |
4 |
. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
F |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
i4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Із центра мас ланки СВ |
проводимо |
|
коло |
радіусом |
z4 . |
|||||||||||||||||||||||||||||||||||||
Результуюча сила |
|
|
|
|
|
прикладена |
|
по дотичній |
|
до цього |
кола |
|||||||||||||||||||||||||||||||
|
|
Fi |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
та |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
s4 |
та |
утворює |
момент |
|||||||||||||||
паралельно |
протилежно |
вектору |
|
|
||||||||||||||||||||||||||||||||||||||
проти |
|
|
|
(напрям |
|
кутового |
прискорення |
|
|
|
|
|
|
|
знайдений |
|||||||||||||||||||||||||||
|
4 |
|
|
|
4 |
|
|
|
||||||||||||||||||||||||||||||||||
за методикою п. 4.5.4.4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Для даної групи невідомими є: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
реакція |
|
|
|
у шарнірі В (за величиною та напрямком); |
|||||||||||||||||||||||||||||||||||||
|
F 23 4 |
|
||||||||||||||||||||||||||||||||||||||||
|
реакція |
|
|
|
у |
|
поступальній |
|
парі |
|
“повзун - стояк” |
|||||||||||||||||||||||||||||||
|
|
F05 |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
(за величиною |
та |
напрямком, |
|
але |
|
відомо, |
що |
вона |
||||||||||||||||||||||||||||||||
|
|
перпендикулярна до осі руху повзуна С); |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
внутрішня реакція F45 F54 в шарнірі С.
1.Розкладаємо реакцію F 23 4 на нормальну та тангенціальну складові:
|
|
|
F |
Fn |
|
F |
|
, |
(5.16) |
|
|
|
|
23 4 |
23 4 |
23 4 |
|
|
|||
|
|
|
|
|
||||||
де |
Fn |
паралельна ланці СВ; |
F |
|
- перпендикулярна до ланки |
|||||
|
23 4 |
|
|
|
|
23 4 |
|
|
|
|
СВ.
66
