
OT_METOD_KP_ONOEOT
.pdf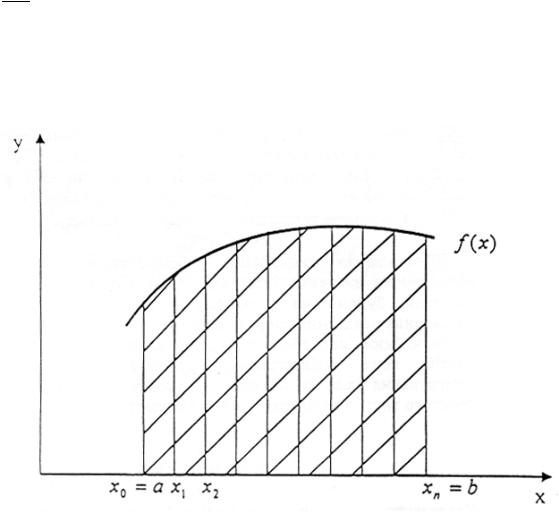
При умові, що a, b - скінчені й підінтегральна функція є неперервною функцією від x на всьому інтервалі [a, b]. З геометричних уявлень визначений інтеграл - це площа фігури, яка окреслена кривою
. віссю X й прямими х=a та x=b (рис. 7.1). Обчислити цю площу можна так: розіб'ємо інтервал інтегрування [а,b] на n стрічок з малим кроком
, на кожному інтервалі довжиною h замінюємо функцію
відрізком прямої (рис.2) й визначаємо площу елементарної стрічки як площу трапеції . При цьому похибка кожної обчисленої елементарної площі визначається заштрихованою не врахованою площею (рис. 7.2)
Рисунок 7.1 - Визначення елементарних стрічок площі підінтегральної функції
80
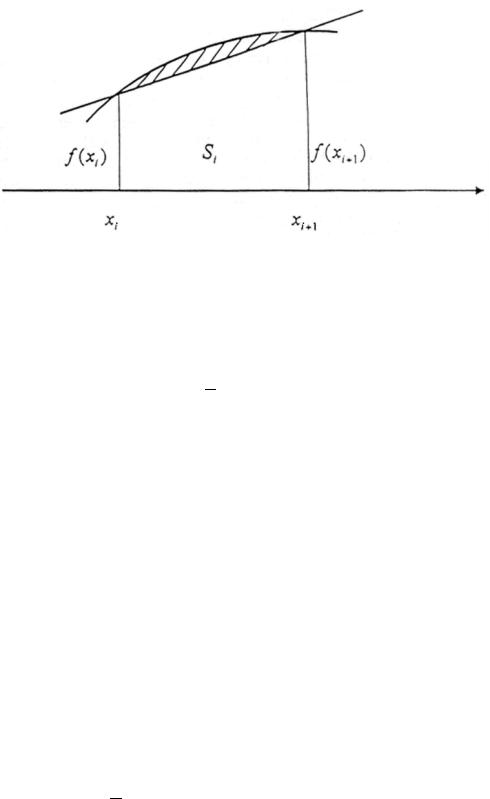
Рисунок 7.2 - Обчислення площі елементарної стрічки
Наближене значення інтеграла є сума усіх елементарних площ , тобто:
2
Після нескладних перетворень маємо квадратурну формулу методу трапецій у вигляді:
|
|
|
|
,де |
|
. тобто |
|
|
|
|
|||
Похибка цієї |
формули може бути |
визначена як |
||||
2 |
|
|
2 |
|||
величина похибки пропорційна квадрату кроку інтегрування.
Похибку обчислення інтегралу можна зменшити за рахунок ускладнення алгоритму метода. Наприклад, замінюючи підінтегральну функцію для двох сусідніх стрічок відрізком параболи, можливо побудувати більш точну квадратурну формулу, формулу Сімпсона, яка має вигляд:
|
/ |
/ |
3 |
4 |
2 |
де n - обов'язково парна кількість стрічок.
Похибка формули Сімпсона визначається виразом ,тобто пропорційна вже четвертій степені кроку інтегрування.
81
Із наведених формул зрозуміло, то точність обчислення значень інтегралів буде тим вища, чим меншим буде крок розбивання інтервалу інтегрування [a, b]. Ця обставина використовується для забезпечення потрібної точності реалізації квадратурних формул, при цьому задаються абсолютною похибкою ε, обчислення інтегралу.
Використовуючи свободу вибору кроку інтегрування |
|
, будують |
|
наступну процедуру забезпечення точності:
1.Визначають початкову кількість кроків п.
2.За допомогою визначеної квадратурної формули обчислюють
значення інтеграла . |
2 . |
3. Подвоюють кількість кроків |
4.Розраховують нове значення інтеграла для п кроків.
5.Перевіряють умову:
||
Якщо ця умова не виконується, то знову виконують п.3,4,5.
Квадратурні Формули Чебишева і Гауса
Для створення квадратурних формул використовуються і інші способи. Наприклад, Чебишев запропонував при побудові квадратурної формули
вибирати абсциси |
, таким чином, шоб: |
; |
1. коефіцієнти |
були рівні поміж себе, тобто |
2.квадратурна формула має бути точною для всіх поліномів до степені n включно.
Зурахуванням другої умови квадратурна формула є точною для
поліномів виду |
0,1,2,…, |
й зокрема для |
1 , |
0 |
. |
З урахуванням, |
|
|
|||
|
першої умови коефіцієнти |
мають значення: |
|
||
|
|
82 |
|
|
|

2
Значення абсцис , обчислюються із рішення системи алгебраїчних рівнянь, яка будується з урахуванням другої умови.
Створена таким чином квадратурна формула зветься формулою
Чебишева. Є таблиці для значень |
(табл. 7.1) |
|
|
|
|||
|
|
Таблиця 7.1 – Значення абсцис за формулою Чебишева |
|||||
|
|
|
|
|
|
|
|
|
п |
3 |
|
4 |
5 |
|
|
|
|
-0,707107 |
|
-0,794654 |
-0,832498 |
|
|
|
|
0 |
|
-0,187592 |
-0,374541 |
|
|
|
|
0,707107 |
|
0,187592 |
0 |
|
|
|
|
- |
|
0,794654 |
0,374541 |
|
|
|
|
- |
|
- |
0,832498 |
|
|
Якщо створювати квадратурну формулу так, щоб вузли |
й |
||||||
коефіцієнти |
, ,…, |
забезпечили точність квадратурної формули, ,…, |
|
||||
|
|
|
|
|
|
|
|
для всіх поліномів найбільш можливої степені п, то будемо мати так звану квадратичну формулу Гауса.
При побудові формули Гауса додатково треба взяти як значення координати нулів полінома Лежандра
|
2 |
1 |
! |
|
|
|
1 , |
0,1,2,… |
|
|
|
|
|
|
|||||||
1; |
|
; |
1 |
3 |
1 ; |
1 |
5 |
3 |
||
|
|
2 |
2 |
|||||||
а коефіцієнти , знайти як рішення системи алгебраїчних рівнянь, побудованої звичайним шляхом. Створені таблиці значень , та формули Гауса, наприклад табл. 7.2.
83
|
|
|
|
Таблиця 2 – Значення |
, та |
за формулою Гауса |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
3 |
|
|
|
4 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
-0,77459667 |
|
|
-0,86113631 |
-0,90617985 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
-0,33998104 |
-0,53846931 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,77459667 |
|
|
|
0,33998104 |
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
- |
|
|
|
0,86113631 |
0,53846931 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
- |
|
|
|
- |
|
0,90617985 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
5/9=0,55555556 |
|
|
0,34785484 |
0,23692688 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
8/9=0,88888889 |
|
|
0,65214516 |
0,47862868 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
5/9=0,55555556 |
|
|
0,65214516 |
0,568888889 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
- |
|
|
|
0,34785484 |
0,47862868 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
- |
|
|
|
- |
|
0,23692688 |
|
|||
|
|
|
|
|
|
|
|
|
|
||||
Для того, щоб використати формулу Чебишева або Гауса для |
|||||||||||||
обчислення інтегралів |
загального |
|
виду |
, |
треба |
зробити заміну |
|||||||
змінної |
|
|
2 |
|
2 |
|
|
|
|
|
|||
Таким чином: |
|
|
|
|
|
|
|
|
|||||
22 2
Застосовуючи відповідні квадратурні формули для обчислення заданого інтегралу, маємо:
формулу Чебишева:
84

формулу Гауса:
2
де
- значення вузлів, які знаходяться із відповідних таблиць. Забезпечення заданої точності обчислення визначених інтегралів
загального типу може бути здійснено одним з двох способів:
1.необхідна точність обчислення досягається за рахунок вибору більшої кількості вузлів п відповідної квадратурної формули;
2.може бути побудована процедура, аналогічна раніше використаній, коли обчислюваний інтеграл записується у вигляді суми двох, чотирьох, восьми й т.д. інтегралів, наприклад:
де кожний інтеграл обчислюється за допомогою квадратурної формули із фіксованою кількістю вузлів n. Значення початкового інтегралу знаходиться як сума:
|
|
,де |
|
, |
1 |
|
|
|
|||
m - кількість ділянок довжиною h, на яку поділяється інтервал |
|||||
інтегрування |
,m подвоюється до того часу, доки не буде |
|
|||
Кількість |
виконуватись |
||||
умова |I |
I | |
ε (n 2n,ε задана похибка обчислень). |
|
||
Контрольні питання
1. Дайте опис методу обчислення визначених інтегралів за допомогою
метода Трапеції.
85
2.Наведіть розрахункову формулу розрахунку інтеграла методом Трапеції.
3.Дайте опис методу обчислення визначених інтегралів за допомогою метода Сіпсона.
4.Наведіть розрахункову формулу розрахунку інтеграла методом Сіпсона.
5.Дайте опис методу обчислення визначених інтегралів за допомогою метода Гауса.
6.Дайте опис методу обчислення визначених інтегралів за допомогою метода Чебишева.
7.Зробіть порівняльний аналіз методів Трапеції та Сімпсона.
8.Зробіть порівняльний аналіз методів Гауса та Чебишева.
86

Комп’ютерний практикум №8
Розв’язок нелінійних рівнянь
Мета
Опанування методи модульної побудови алгоритмів та їх реалізації за допомогою складних елементів алгоритмічної мови. Засвоїти методи розв’язоку нелінійних рівнянь.
Робоче завдання
Навчитись знаходити корені нелінійних рівнянь за допомогою методів Хорд та Ньютона.
Хід роботи
Написати програму для знаходження коренів рівняння.
Варіанти завдань
№ |
|
Рівняння |
|
|
Інтервал |
Метод |
№ |
|
Рівняння |
|
|
Інтервал |
Метод |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
ln |
|
|
|
|
|
[0.5;1] |
Хорд |
12 |
|
1 |
|
|
|
|
[0.2;0.3] |
Хорд |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
2 |
|
sin |
|
|
|
|
|
[0;1] |
Ньютона |
13 |
|
|
|
[0.5;1] |
Ньютона |
||||
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
|
|
3 |
|
cos |
|
|
|
|
|
[0.5;1] |
Хорд |
14 |
|
|
|
|
|
|
[0;1] |
Хорд |
|
|
|
7 |
|
8 |
|
|
|
|
|
sin |
|
|
|
|
|
|
|
||
4 |
|
|
|
6 |
[3;4] |
Ньютона |
15 |
|
cos |
7 |
|
8 |
|
[0.5;1] |
Ньютона |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|||
5 |
|
sin |
0 |
|
|
[0.5;1] |
Хорд |
16 |
|
|
|
[3;4] |
Хорд |
||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
[0.2;0.3] |
Ньютона |
17 |
|
1 |
|
|
[0.5;1] |
Ньютона |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7 |
2 |
2 |
|
|
[0.2;0.3] |
Хорд |
18 |
|
|
|
0 |
|
|
[0.2;0.3] |
Хорд |
||||
|
cos 1.57 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
||||||
8 |
|
|
|
5 |
[0;1] |
Ньютона |
19 |
|
|
|
[0.2;0.3] |
Ньютона |
|||||||
|
|
|
|
|
|
||||||||||||||
|
|
10 |
16 |
|
|
|
|
2 |
cos 1.57 |
|
|
|
|
||||||
9 |
|
ln |
4 |
|
|
[1.5;2] |
Хорд |
20 |
|
|
[0;1] |
Хорд |
|||||||
|
|
|
|
|
|
|
|
10 |
16 |
|
5 |
|
|
||||||
10 |
|
3 |
6 |
8 |
|
[0;2] |
Ньютона |
21 |
|
|
[1.5;2] |
Ньютона |
|||||||
|
|
|
|
|
|
|
ln |
4 |
8 |
|
|
|
|||||||
11 |
|
|
|
|
|
[0.2;0.3] |
Хорд |
22 |
|
|
[0;2] |
Хорд |
|||||||
2 |
cos 1.57 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
3 |
6 |
|
|
|
||||||||
Стислі теоретичні відомості
Нехай маємо рівняння |
0, в яком функція |
визначена, не має |
розривівтаінших особливостей навідрізку [a, b].
87
Будь-яке значення (х=S), що надає функції нульове значення
0 називається коренем рівняння. Будемо вважати, що функція має ізольовані корені. Це означає, що для кожногокоренярівнянняіснуєдеяказона, вякійнемає інших коренів. Наближені числові методивизначення коренів рівняньздебільшого складаються з двох етапів. На першому етапі відокремлюються корені, тобто
визначаються можливо найбільш вузькі проміжки |
, в кожному з яких |
||||||||||
знаходиться лише один корінь. На другому етапі приблизно, |
знайдені корені |
||||||||||
доводяться до заданої точності. |
|
|
|
||||||||
Для визначення коренів слід керуватися наступною теоремою. |
|||||||||||
Теорема: Якщо неперервна функція |
змінює знак на межах відтинку |
||||||||||
, |
тобто |
|
|
|
|
, то всередині цього відтинку знаходиться |
|||||
щонайменше, |
один корінь |
рівняння. Він буде обов'язково єдиний, якщо похідна |
|||||||||
0 |
|
|
|
|
|||||||
` |
в межах відтинку |
коли, |
|
існує й зберігає незмінним свій знак, тобто якщо |
|||||||
` |
0 |
або |
` |
0 |
а |
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
Відокремлювати корені можна різними способами: аналітично, тобто використовуючи наведену теорему, графічно, тобто побудувавши графік зміни
значень функції |
на заданому інтервалі визначення й таким чином |
||||
знаходячи інтервали |
близько нулів побудованого графіка та ін. Можна |
||||
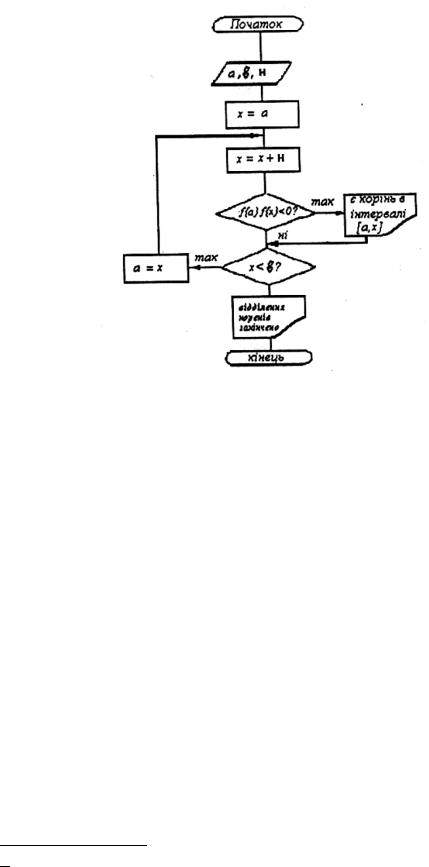
використати комп’ютерні, алгоритми. Приклад такого алгоритму наведений на |
|||||
рис. 8.1. Його ідея полягає в тому, що заданий інтервал визначення |
треба |
||||
послідовно переглянути з довільно вибраним кроком h, кожен раз, визначаючи, |
|||||
знаки функції |
на кінцях відтинків |
|
вочевидь мають |
||
|
. Ті малі відтинки, у яких функція, |
має різні знаки, , |
|||
1 , |
2 |
… |
|||
|
|
|
|
|
|
хоча б один корінь і фіксуються. Після цього корені уточнюються до заданої точності якимось з методів. Доречі, цього можна досягти використавши описаний алгоритм, відповідно зменшуючи крок h тим самим рекурентно звужуючи відтинок, але це не дуже ефективний метод і здебільшого використовуються ітераційні методи а саме: метод хорд або метод дотичних (Ньютона).
88
|
Рисунок 8.1 – Алгоритм відокремлення коренів |
|
||||
Ітераційний |
метод |
полягає у |
тому, що |
рівняння |
початкове |
|
перетворюється на еквівалентне виду |
. Далі, |
прийнявши |
||||
0 |
||||||
наближення |
або |
обчислюється значення |
. Оскільки |
|||
дорівнює х, воно приймається за наступне наближення до кореня й описані дії повторюються. Водночас виконується порівняння попереднього й уточненого значення х, якщо їх різниця по абсолютній величині не перевищує константи точності , задана точність вважається досягнутою, процес обчислень переривається. Цей метод працює досить ефективно, але лише в разі влучного
перетворення початкового рівняння |
у вид |
, |
а тому таке |
|||
перетворення слід робити людині вручну, а0 |
не програмно за |
допомогою |
||||
комп'ютера. Наприклад, якщо |
0 у вид |
, |
то перетворення |
|||
рівняння |
|
|
|
|
буде |
|
|
|
|
|
|||
невдалим, бо ітераційний процес розійдеться. Якщо ж перетворити його у
, то ітераційний процес зійдеться. З цього прикладу
неважко зрозуміти, при наближеному, а не точному значенні х нев’язка рівняння буде залежати головним чином від члену полінома з найвищим степенем, і саме
89
