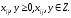Задача про виробництво (складність 3).
Постановка задачі. Завод виготовляє виріб, який складається з 3-ох видів деталей. Для виготовлення кожної деталі можна використовувати кожний з 2-х видів верстатів. Час, необхідний для виготовлення однєї деталі на кожному з верстатів та фонд робочого часу, наведений в таблиці 3.15.
За технологією виробництва (рисунок 3.10) для готового виробу необхідно 2 деталі 1-ого типу, 3 деталі 2-ого типу та 1 деталь 3-ого типу. Вважаємо, що для збору готового виробу з деталей, часу не потрібно.
Необхідно знайти таку кількість деталей, при якій кількість готових виробів, які вготовляються протягом доби, була максимальною.
Таблиця 3.15
|
|
Час виготовлення однієї деталі, в хвилинах |
Фонд робочого часу, в годинах | |||
|
|
|
|
| ||
|
Верстат 1 |
5 |
3 |
6 |
10 | |
|
Верстат 2 |
4 |
5 |
3 |
14 | |
Рисунок
3.10 – Технологія виробництва
Побудова математичної моделі.
Змінні:
–кількість
готових виробів;
-
кількість деталей i-того
типу, яку необхідно виготовляти (
)
наj-ому
верстаті (
).
Цільова функція: максимізувати кількість готових виробів:
Обмеження:
на кількість деталей 1-ого типу:
на кількість деталей 2-ого типу:
на кількість деталей 3-ого типу:
на робочий час 1-ого верстату:
на робочий час 2-ого верстату:
на невід’ємність і цілочисельність:
