
- •Знайти екстремум функції за умови.
- •4. Знайти екстремум функції за умови .
- •Знайти екстремуми функції .
- •Знайти розв’язок задачі Коші
- •Знайти екстремум функції за умови .
- •2. Показати, що поле потенціальне та знайти його потенціал.
- •5. Знайти розв’язок задачі Коші
- •Знайти масу кардіоїди , якщо лінійна густина маси .
- •Знайти потік векторного поля через зовнішню сторону поверхні тіла, обмеженого поверхнями
- •Знайти найбільше та найменше значення функції в області .
- •Знайти потік векторного поля через зовнішню сторону поверхні тіла, обмеженого поверхнями
- •Знайти розв’язок задачі Коші
- •Знайти екстремум функції за умови .
- •Знайти розв’язок задачі Коші .
№ 1
1. Заміна змінних в кратних інтегралах. Подвійний інтеграл в полярній системі координат.
2.
Знайти циркуляцію поля
![]() вздовж замкненого контуру С:
вздовж замкненого контуру С:
![]() ,
який обходиться проти годинникової
стрілки.
,
який обходиться проти годинникової
стрілки.
3.
Знайти
потік векторного поля
![]() через внутрішню сторону частини поверхні
через внутрішню сторону частини поверхні
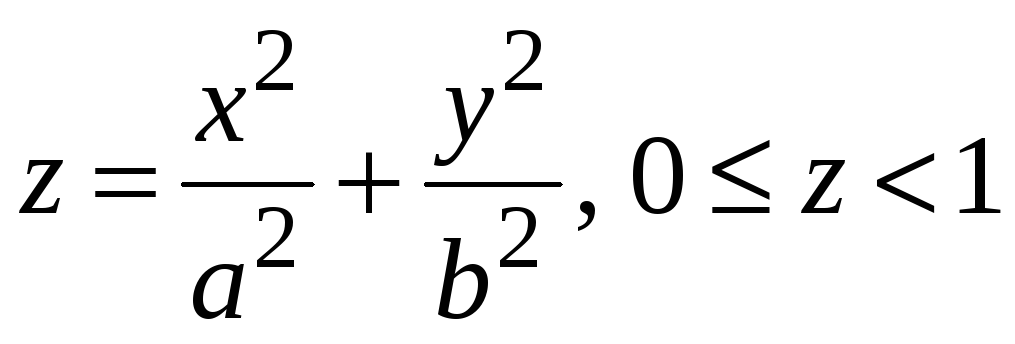 ,
яка розташована в першому октанті.
,
яка розташована в першому октанті.
4.
Знайти
екстремуми функції
![]() .
.
5.
Знайти
розв’язок задачі Коші
![]() .
.
№ 2
1. Диференціювання складеної функції багатьох змінних. Повна похідна функції.
2.
Показати, що поле
![]() потенціальне та знайти його потенціал.
потенціальне та знайти його потенціал.
3.
Знайти
потік векторного поля
![]() через зовнішню сторону поверхні тіла,
обмеженого поверхнями
через зовнішню сторону поверхні тіла,
обмеженого поверхнями
![]()
![]()
![]() .
.
4.
Знайти
екстремум функції
![]() за умови
за умови
![]() .
.
5.
Знайти
розв’язок задачі Коші
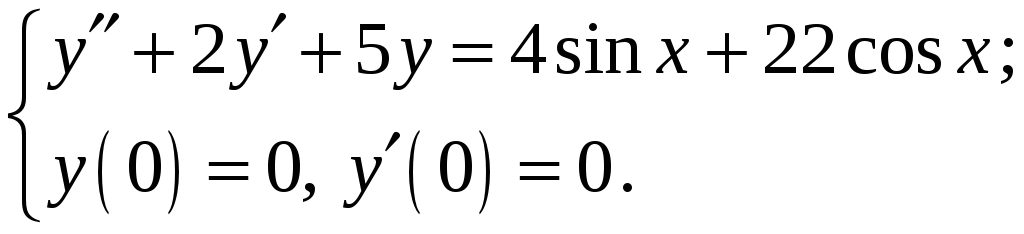
№ 3
1. Деякі типи ДР: диференціальні рівняння першого порядку з відокремленими та відокремлюваними змінними; однорідні ДР першого порядку.
2.
Показати,
що поле
![]() потенціальне та знайти його потенціал.
потенціальне та знайти його потенціал.
3.
Знайти
масу частини поверхні
![]() ,
яка відтинається від неї циліндром
,
яка відтинається від неї циліндром
![]() при заданій поверхневій густині маси
при заданій поверхневій густині маси
![]() .
.
4.
Знайти
найбільше та найменше значення функції
![]() в області
в області
![]()
5.
Знайти
розв’язок задачі Коші
![]()
![]() .
.
№ 4
1. Задача про обчислення маси матеріальної кривої. Криволінійні інтеграли І роду (по довжині дуги). Означення та обчислення, фізичний зміст та властивості. Криволінійні інтеграли І роду (по довжині дуги): означення, умови існування, фізична зміст та обчислення.
2.
Знайти масу кардіоїди
![]() ,
якщо лінійна густина маси
,
якщо лінійна густина маси
![]() .
.
3.
Знайти
потік векторного поля
![]() через зовнішню сторону поверхні тіла,
обмеженого поверхнями
через зовнішню сторону поверхні тіла,
обмеженого поверхнями
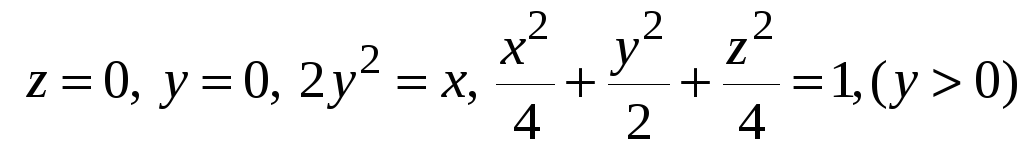 .
.
4.
Знайти
екстремуми функції
![]() .
.
5.
Знайти
криву, для якої довжина відрізка, що
його нормаль відтинає від осі ОХ, дорівнює
![]() .
.
№ 5
-
Означення ФСР ОЛДР n-го порядку. Необхідні та достатні умови існування такої системи.
-
Показати, що поле
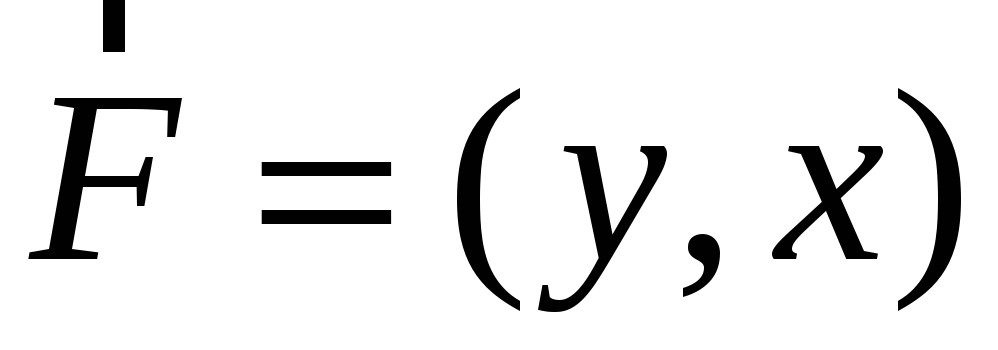 потенціальне та знайти роботу поля при
переміщенні матеріальної точки від
точки А(-1,2) до В(2,3).
потенціальне та знайти роботу поля при
переміщенні матеріальної точки від
точки А(-1,2) до В(2,3). -
Знайти масу частини однорідної поверхні
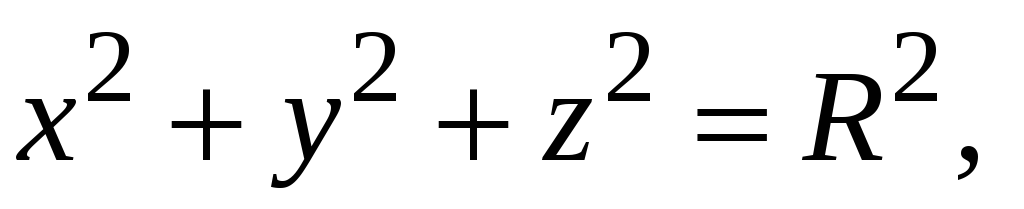 яка
відтинається від неї поверхнями
яка
відтинається від неї поверхнями
 ,
,
 перший
октант.
перший
октант. -
Знайти екстремум функції
 за умови
за умови
 .
.
5.
Знайти
розв’язок задачі Коші

№ 6
-
Задача про роботу змінної сили по переміщенню матеріальної точки вздовж кривої. Криволінійні інтеграли ІІ роду (за координатами). Означення та фізичний зміст, властивості. Криволінійні інтеграли ІІ роду загального виду.
-
Знайти масу однієї арки циклоїди
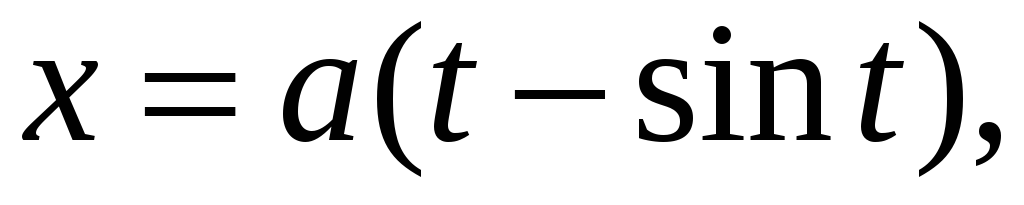
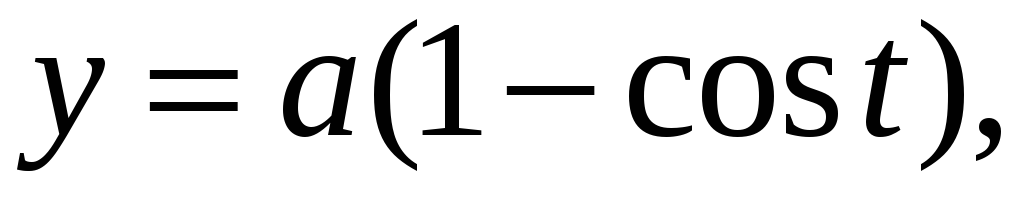
 якщо
лінійна густина маси
якщо
лінійна густина маси
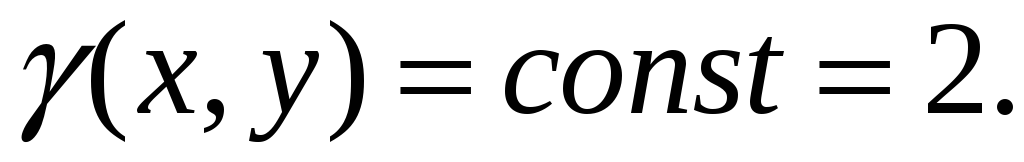
-
Знайти потік векторного поля
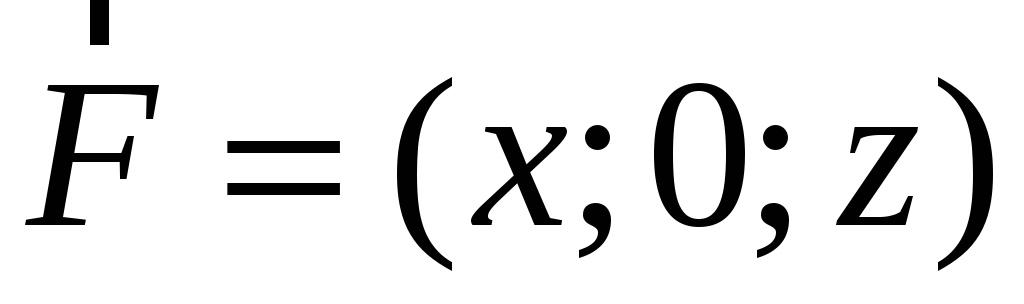 через зовнішню сторону поверхні тіла,
обмеженого поверхнями
через зовнішню сторону поверхні тіла,
обмеженого поверхнями
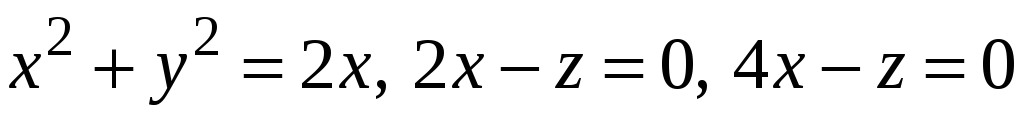 .
. -
Знайти площу фігури, обмеженої лініями
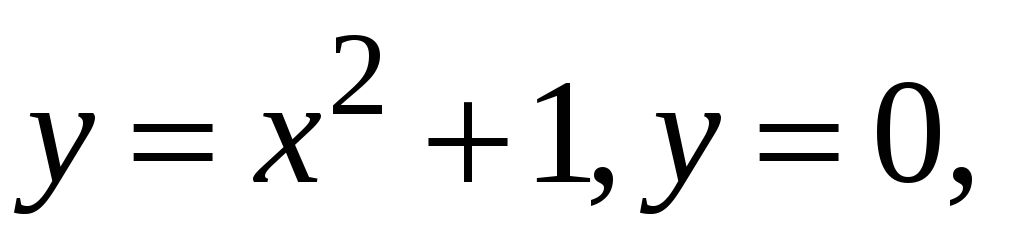
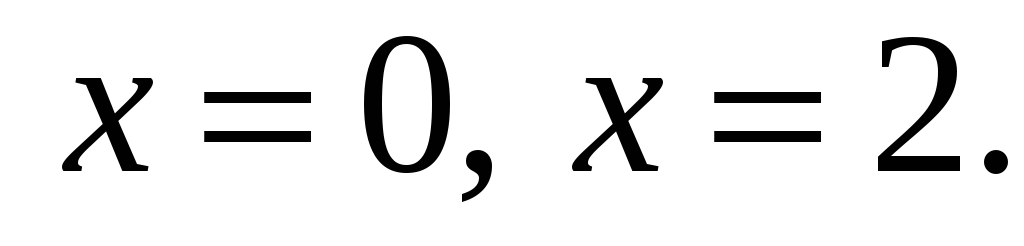
-
Знайти розв’язок задачі Коші
 .
.
№ 7
-
Потенціальні векторні поля та їх властивості. Скалярний потенціал векторного поля: означення та його обчислення. Необхідна і достатня ознака потенціальності векторного поля.
-
При заданій густині заряду
 знайти заряд, розподілений вздовж
відрізка прямої від А(0,0) до В(4,3).
знайти заряд, розподілений вздовж
відрізка прямої від А(0,0) до В(4,3). -
Знайти потік векторного поля
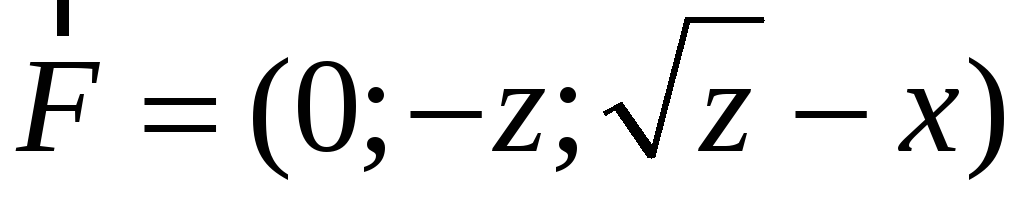 через зовнішню сторону частини поверхні
через зовнішню сторону частини поверхні

-
Знайти екстремум функції

-
Знайти розв’язок задачі Коші
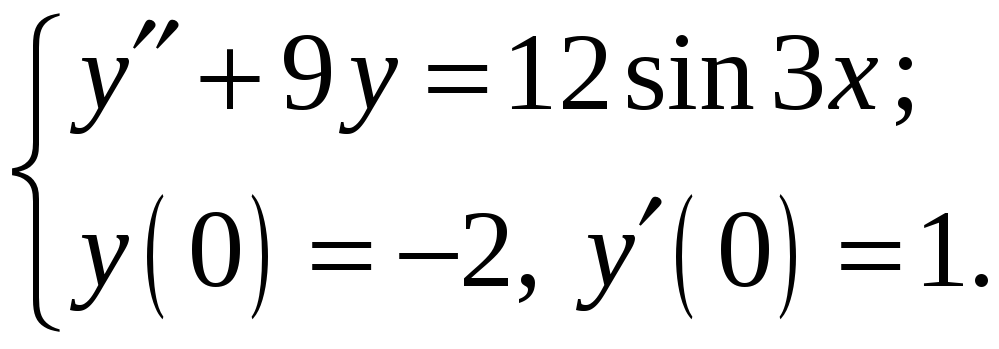
№ 8
-
Зв’язність області. Формула Гріна: формулювання та доведення.
-
Знайти масу заряду, розподіленого вздовж астроїди
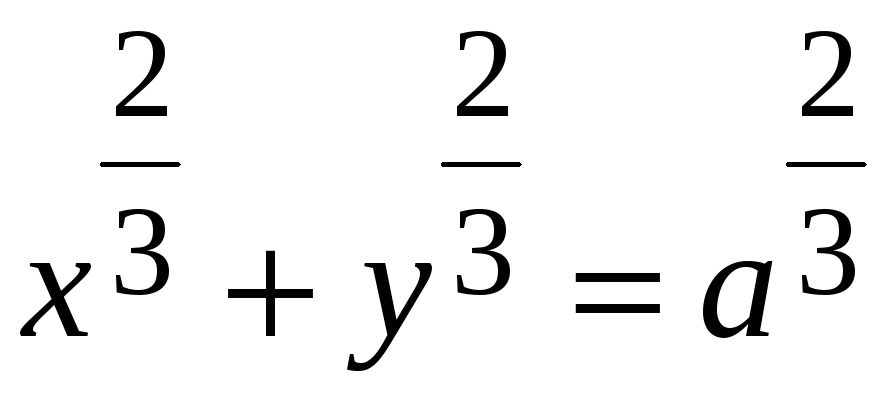 ,
якщо лінійна густина заряду
,
якщо лінійна густина заряду
 .
. -
Знайти потік векторного поля
 через внутрішню частину поверхні
через внутрішню частину поверхні
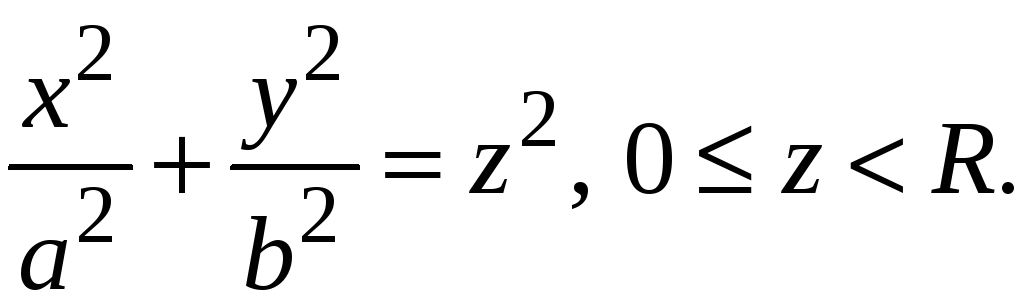
-
Знайти екстремуми функції
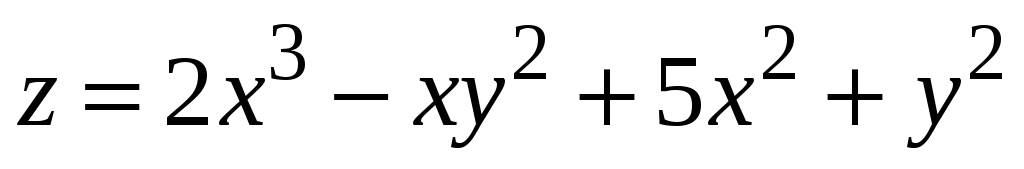 .
. -
Знайти розв’язок задачі Коші
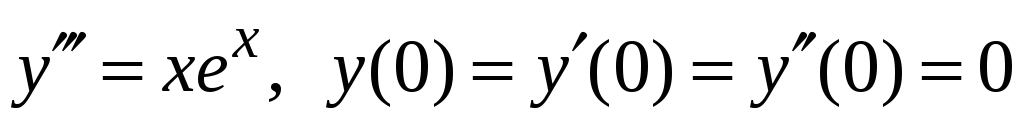 .
.
№ 9
1. ОЛДР n-го порядку: ФСР, структура загального розв’язку, формула Остроградського-Ліувілля.
2.
Знайти
циркуляцію поля
![]() вздовж кола
вздовж кола
![]() ,
яке обходиться проти годинникової
стрілки.
,
яке обходиться проти годинникової
стрілки.
3.
Знайти
потік векторного поля
![]() через
зовнішню сторону частини поверхні
через
зовнішню сторону частини поверхні
![]() , яка розташована в І октанті .
, яка розташована в І октанті .
4.
Знайти
найбільше та найменше значення функції
![]() в області
в області
![]() .
.
5.
Знайти
розв’язок задачі Коші

№ 10
1. ДР n-го порядку: загальний вигляд; задача Коші; загальний розв'язок; теорема Коші. Існування та єдиність розв’язку задачі Коші.
2.
Знайти роботу сили
![]() ,
яка виконується при переміщенні
матеріальної точки вздовж ламаної
,
яка виконується при переміщенні
матеріальної точки вздовж ламаної
![]() , якщо
, якщо
![]() .
.
3.
Знайти
потік векторного поля
![]() через
зовнішню сторону поверхні тіла, обмеженого
поверхнями
через
зовнішню сторону поверхні тіла, обмеженого
поверхнями
![]()
4.
Знайти
екстремум функції
![]() .
.
5.
Знайти
розв’язок задачі Коші

№ 11
1. Потенціальні та соленоїдальні векторні поля: означення та їх властивості. Векторні труби.
2.
Знайти
масу заряду , розподіленого вздовж лінії
![]() якщо
задана густина заряду
якщо
задана густина заряду
![]() .
.
3.
Знайти
потік векторного поля
![]() через
зовнішню сторону поверхні тіла, обмеженого
поверхнями
через
зовнішню сторону поверхні тіла, обмеженого
поверхнями
![]()
4.
Знайти
найбільше та найменше значення функції
![]() в області
в області
![]()
5.
Знайти
розв’язок задачі Коші
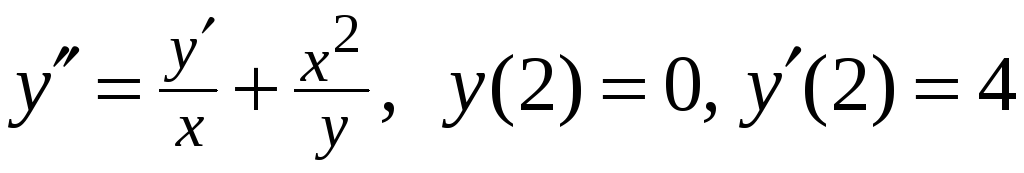
№ 12
1. Поняття подвійного інтегралу, його обчислення по прямокутній та довільній області. Геометричний зміст. Фізичні застосування подвійного інтеграла. Теорема про середнє в подвійному інтегралі.
2.
Знайти масу петлі кривої
![]() (першої
арки), якщо лінійна густина маси дорівнює
(першої
арки), якщо лінійна густина маси дорівнює
![]() .
.
3.
Знайти
потік векторного поля
![]() через зовнішню сторону частини поверхні
через зовнішню сторону частини поверхні
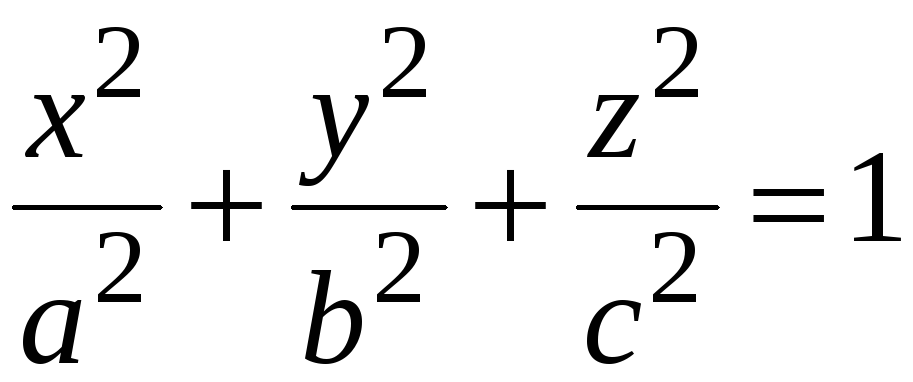 ,
якщо
,
якщо
![]() .
.
4.
Знайти
екстремуми функції
![]() .
.
5.
Знайти
розв’язок задачі Коші
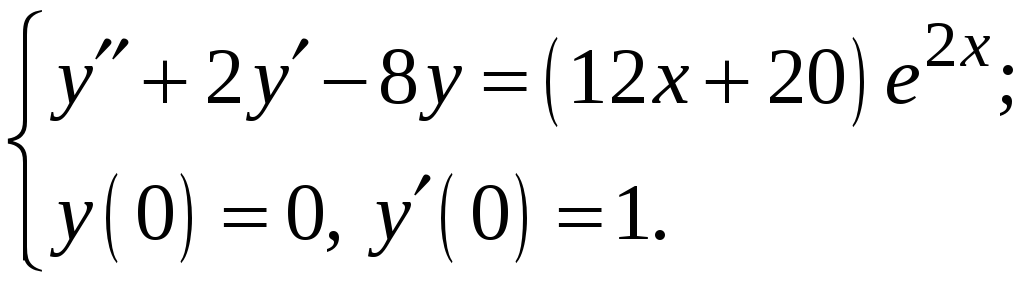
№ 13
-
Поняття подвійного інтегралу Рімана по області, необхідна умова існування, класи інтегрованих функцій, геометричний та фізичний зміст. Властивість лінійності в подвійному інтегралі.
-
Знайти масу дуги лінії
 від
від
 до
до
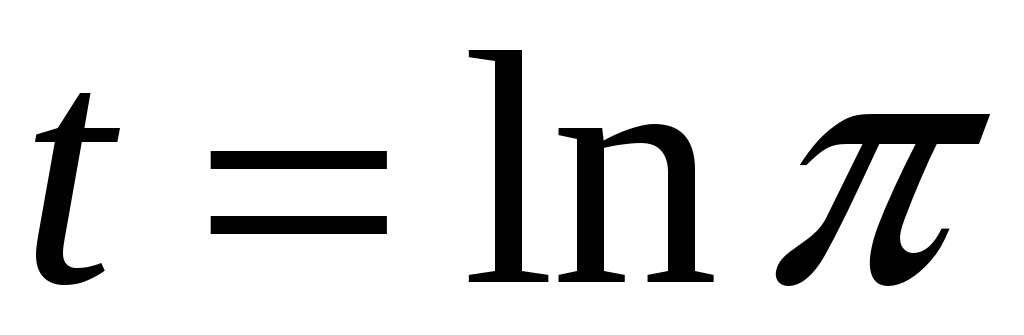 ,
якщо лінійна густина маси
,
якщо лінійна густина маси

-
Знайти потік векторного поля
 через внутрішню сторону частини поверхні
через внутрішню сторону частини поверхні
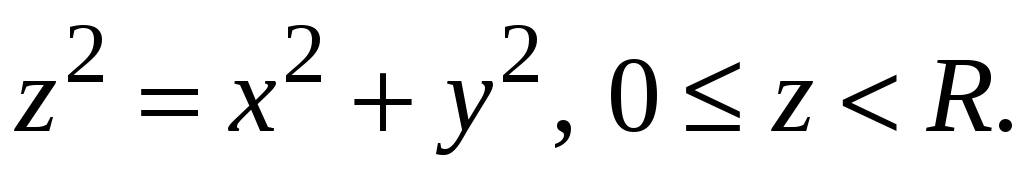
-
Знайти екстремум функції
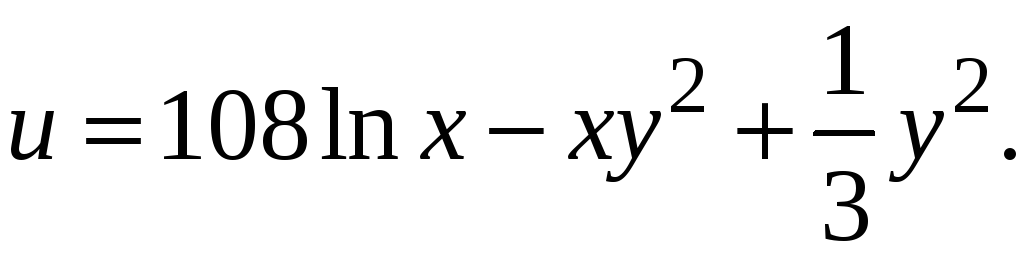
-
Знайти розв’язок задачі Коші

№ 14
1. Заміна змінних в кратних інтегралах. Потрійний інтеграл в циліндричних і сферичних координатах.
2.
Знайти циркуляцію поля
![]() вздовж замкненого контуру С:
вздовж замкненого контуру С:
![]() ,
який обходиться проти годинникової
стрілки.
,
який обходиться проти годинникової
стрілки.
3.
Знайти
потік векторного поля
![]() через внутрішню сторону частини поверхні
через внутрішню сторону частини поверхні
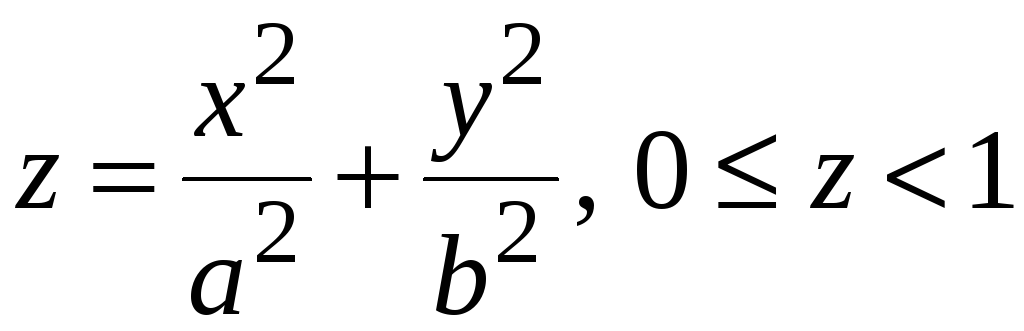 ,
яка розташована в першому октанті.
,
яка розташована в першому октанті.
4.
Знайти
екстремуми функції
![]() .
.
5.
Знайти
розв’язок задачі Коші
![]() .
.
№ 15
1. Частинний та повний прирости функції в точці. Частинні похідні функцій багатьох змінних та їх геометричний зміст при n=2. Диференційованість функції багатьох змінних в точці (означення). Необхідна та достатня умови диференційовності функції. Диференціал функції.
2.
Знайти координати центра ваги однорідної
дуги циклоїди
![]() ,
якщо
,
якщо
![]() .
.
3.
Знайти
потік векторного поля
![]() через
зовнішню сторону частини поверхні
через
зовнішню сторону частини поверхні
![]()
-
Знайти екстремум функції за умови.
№ 16
1. Формула Тейлора для функції багатьох змінних.
2.
Знайти масу дуги кубічної параболи
![]() ,
якщо лінійна густина маси дорівнює
,
якщо лінійна густина маси дорівнює
![]() .
.
3.
Знайти потік векторного поля
![]() через внутрішню сторону частини поверхні
через внутрішню сторону частини поверхні
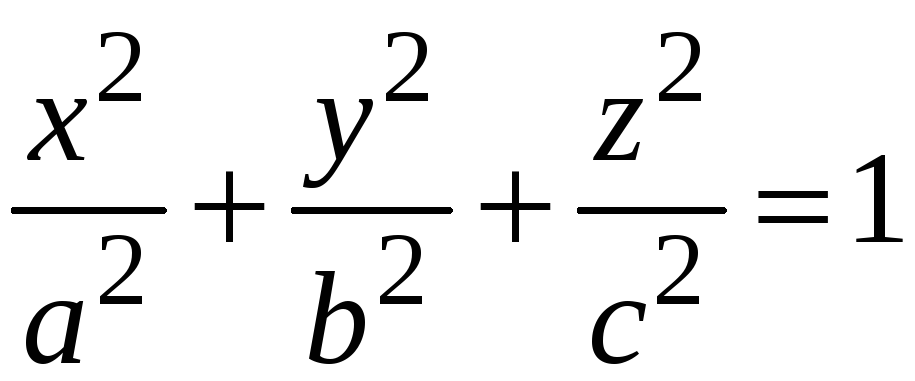 ,
яка розташована у І октанті.
,
яка розташована у І октанті.
4. Знайти екстремум функції за умови .
5.
Знайти загальний розв’язок рівняння
![]()
№ 17
1. Локальний екстремум функції багатьох змінних: означення, необхідна та достатня умови існування.
2.
Знайти роботу сили
![]() ,
яка виконується при переміщенні
матеріальної точки вздовж дуги
,
яка виконується при переміщенні
матеріальної точки вздовж дуги
 в напрямку зростання параметру.
в напрямку зростання параметру.
3.
Знайти масу частини поверхні
![]() ,
яка відтинається від неї поверхнями
,
яка відтинається від неї поверхнями
![]() ,
(І октант), якщо поверхнева густина маси
дорівнює
,
(І октант), якщо поверхнева густина маси
дорівнює

4.
Знайти екстремум функції
![]() .
.
5.
Зінтегрувати диференціальне рівняння:
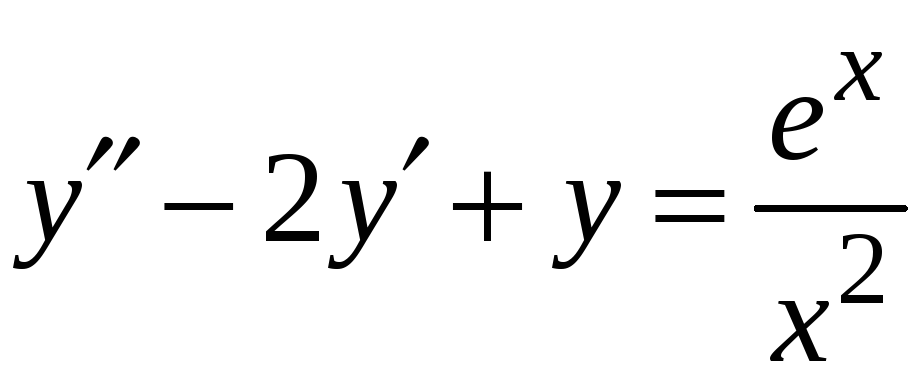
№ 18
1. Існування неявно заданої функції та її диференціювання.
2.
При заданій лінійній густині заряду
![]() знайти
масу заряду, розподіленого вздовж лінії,
яка задана параметрично
знайти
масу заряду, розподіленого вздовж лінії,
яка задана параметрично
![]()
![]() .
.
3.
Знайти потік векторного поля
![]() через зовнішню сторону поверхні тіла,
обмеженого поверхнями
через зовнішню сторону поверхні тіла,
обмеженого поверхнями
![]()
4.
Знайти екстремум функції
![]() за умови
за умови
![]()
5.
Знайти розв’язок задачі Коші
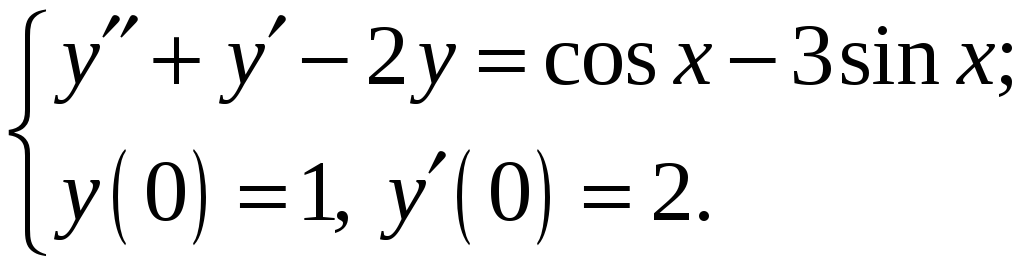
№ 19
1. Квадратична форма n-змінних: означення, знаковизначеність. Критерій Сильвестра.
2.
Показати, що поле
![]() потенціальне та знайти його потенціал.
потенціальне та знайти його потенціал.
3.
Знайти масу частини однорідної поверхні
![]() ,
яку відтинає від неї поверхня
,
яку відтинає від неї поверхня
![]()
4.
Знайти екстремуми функції
![]() .
.
5.
Зінтегрувати диференційне рівняння:
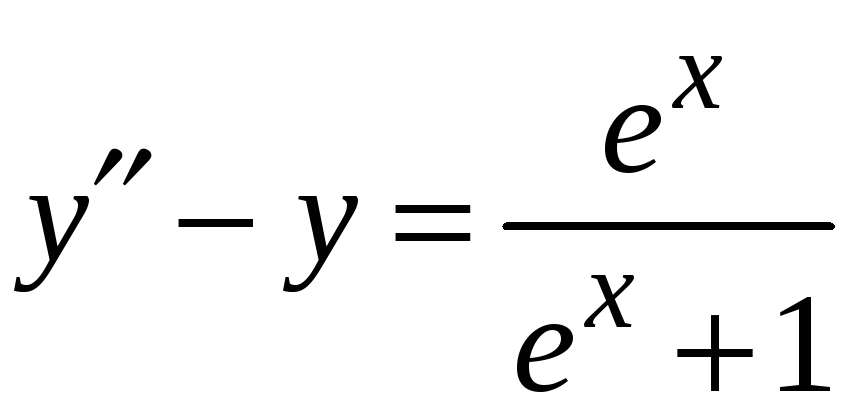 .
.
№ 20
-
Однорідні функції. Однорідні диференціальні рівняння 1-го порядку та ті, що зводяться до них.
-
При заданій густині заряду
 знайти заряд, розподілений вздовж
відрізка прямої від А(0,0) до В(4,3).
знайти заряд, розподілений вздовж
відрізка прямої від А(0,0) до В(4,3). -
Знайти потік векторного поля
 через зовнішню сторону частини поверхні
через зовнішню сторону частини поверхні

-
Знайти екстремум функції

-
Знайти розв’язок задачі Коші
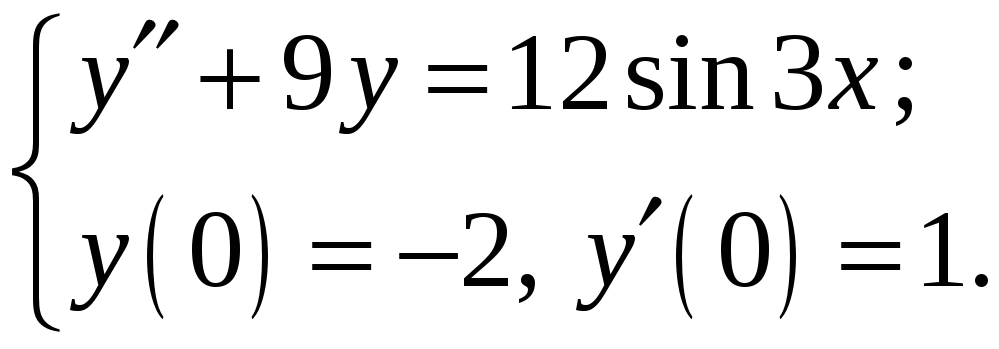
№ 21
1. Дивергенція векторного поля: означення та її властивості. Формула Остроградського-Гауса в координатній і векторній формі.
2.
Показати, що поле
![]() потенціальне та знайти його потенціал.
потенціальне та знайти його потенціал.
3.
Знайти масу однорідної частини поверхні
![]() ,
вирізаної з неї поверхнями
,
вирізаної з неї поверхнями
![]() (І
октант).
(І
октант).
4.
Знайти умовні екстремуми функції
![]() за умови
за умови
![]()
5.
Знайти розв’язок задачі Коші
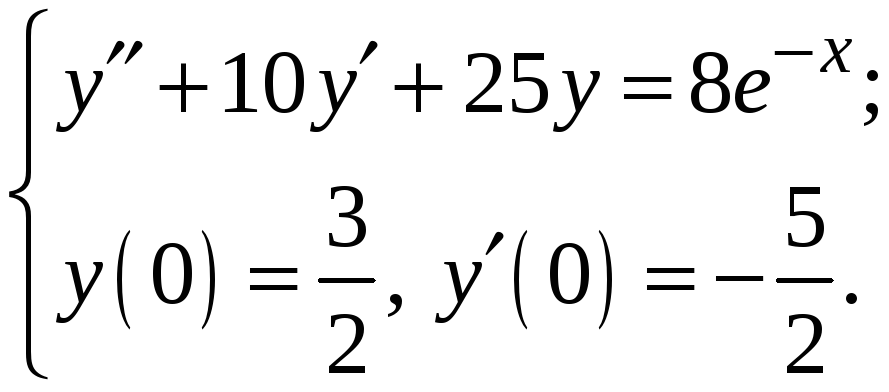
№ 22
1. Лінійно залежні і лінійно незалежні системи функцій. Визначник Вронського для лінійно-залежних систем функцій.
2.
При заданій лінійній густині маси
![]() ,
знайти масу лінії
,
знайти масу лінії
![]()
3.
Знайти потік векторного поля
![]() через внутрішню частину поверхні
через внутрішню частину поверхні
 ,
яка розташована у першому октанті.
,
яка розташована у першому октанті.
4.
Знайти екстремуми функції
![]()
5.
Знайти загальний розв’язок рівняння
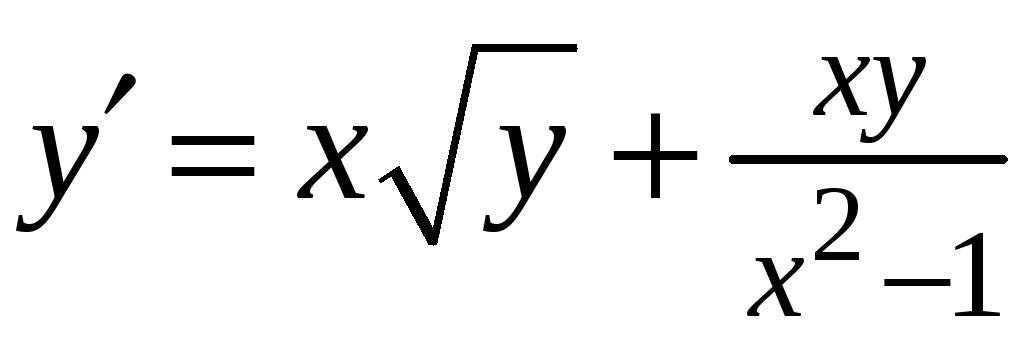
№ 23
1. Площа криволінійної поверхні: означення та її обчислення за допомогою подвійного та поверхневого інтегралів.
2.
Знайти роботу сили
![]() ,
при переміщенні матеріальної точки
вздовж дуги
,
при переміщенні матеріальної точки
вздовж дуги
![]() ,
якщо
,
якщо
![]() .
.
3.
Знайти
потік радіус-вектора точки через зовнішню
сторону поверхні тіла, обмеженого
поверхнями
![]()
![]()
4.
Знайти
екстремуми функції
![]() .
.
5.
Знайти
розв’язок задачі Коші
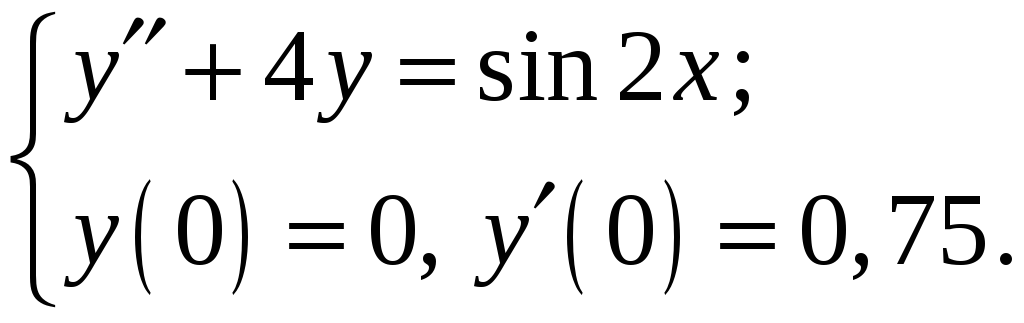
№ 24
1. Умовний екстремум функції багатьох змінних: означення, необхідна умова існування. Обчислення методом виключення і Лагранжа.
2.
Показати, що поле
![]() потенціальне та знайти його потенціал.
потенціальне та знайти його потенціал.
3.
Знайти
потік векторного поля
![]() через зовнішню сторону поверхні тіла,
обмеженого поверхнями
через зовнішню сторону поверхні тіла,
обмеженого поверхнями
![]()
4.
Знайти
екстремуми функції
![]() .
.
5.
Знайти
розв’язок задачі Коші
![]() .
.
№ 25
1. Диференціальні операції другого порядку в стаціонарних та векторних полях.
2.
Знайти масу петлі кривої
![]() (першої арки), якщо лінійна густина маси
дорівнює
(першої арки), якщо лінійна густина маси
дорівнює
![]() .
.
3.
Знайти
потік векторного поля
![]() через зовнішню сторону частини поверхні
через зовнішню сторону частини поверхні
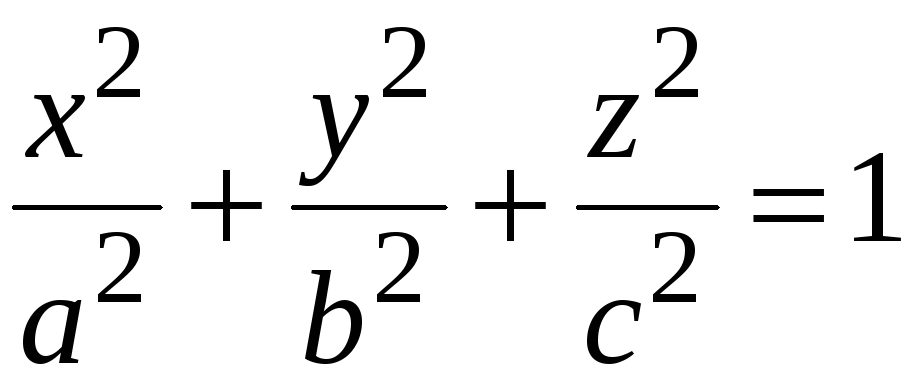 ,
якщо
,
якщо
![]() .
.
4.
Знайти
екстремуми функції
![]() .
.
5.
Знайти
розв’язок задачі Коші
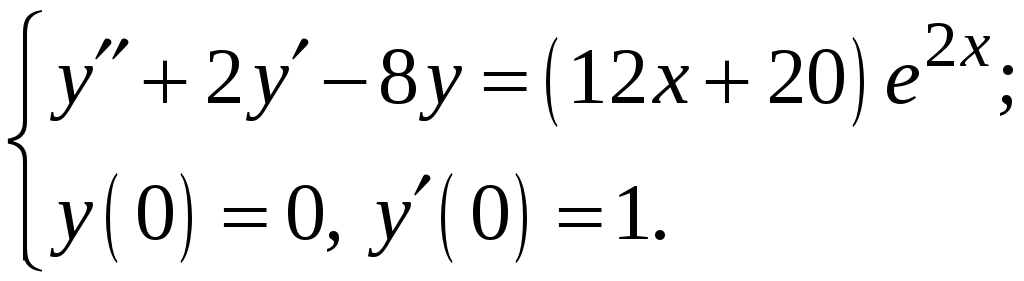
№ 26
1. Потрійний інтеграл: означення та обчислення зведенням до повторного. Геометричний та фізичний зміст. Застосування потрійних інтегралів в механіці.
2.
Знайти роботу сили
![]() ,
при переміщенні матеріальної точки
вздовж прямої від точки А(1,1,1) до точки
В(2,3,4).
,
при переміщенні матеріальної точки
вздовж прямої від точки А(1,1,1) до точки
В(2,3,4).
3.
Знайти
масу однорідних частин поверхні кулі
![]() ,
які відтинаються від неї циліндром
,
які відтинаються від неї циліндром
![]() .
.
4.
Знайти
екстремуми функції
![]() .
.
5.
Зінтегрувати
диференційне рівняння:
![]()
№ 27
1. Скалярне поле. Похідна скалярного поля за напрямом. Градієнт скалярного поля та його властивості.
2.
Знайти масу всієї кардіоїди
![]() ,
якщо лінійна густина маси
,
якщо лінійна густина маси
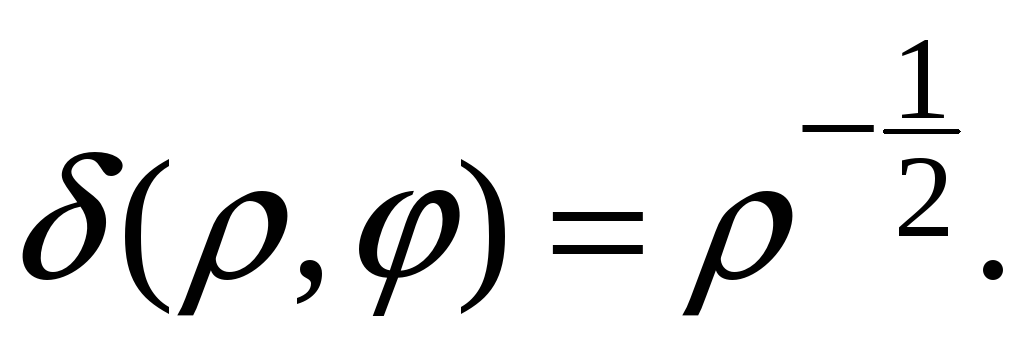
3.
Знайти потік векторного поля
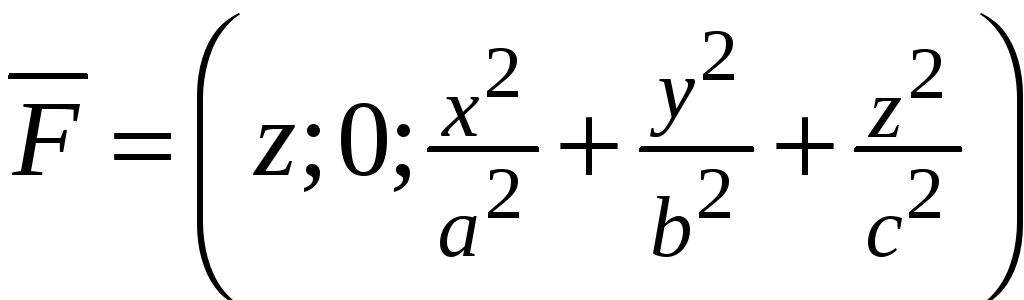 через зовнішню сторону частини поверхні
через зовнішню сторону частини поверхні
 ,
яка розташована у І октанті.
,
яка розташована у І октанті.
4.
Знайти екстремуми функції
![]() за умови
за умови
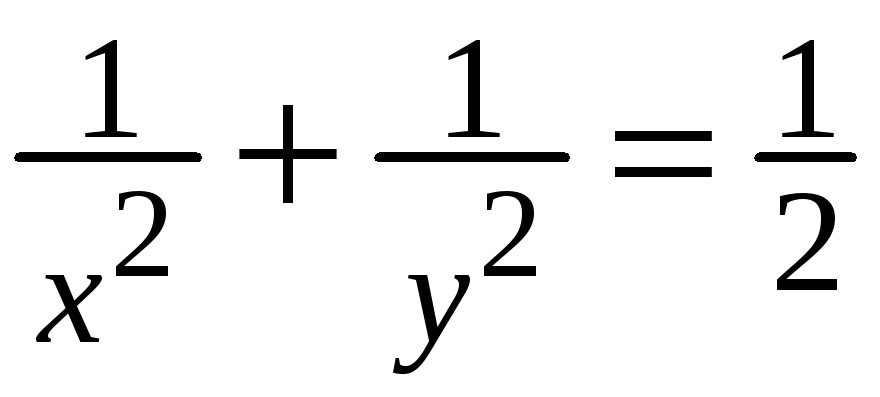 .
.
5.
Знайти криві, для яких площа трикутника,
утвореного віссю ОХ, дотичною і
радіус-вектором точки дотику, стала і
дорівнює
![]() .
.
№ 28
1. Дотична площина і нормаль до поверхні. Геометричний зміст диференціалу двох змінних.
2.
Показати, що поле
![]() потенціальне та знайти його потенціал.
потенціальне та знайти його потенціал.
3.
Знайти центр ваги частини поверхні
параболоїда
![]() ,
яка відтинається від нього площиною
,
яка відтинається від нього площиною
![]() ,
якщо поверхнева густина маси обернено
пропорційна до
,
якщо поверхнева густина маси обернено
пропорційна до
![]() .
.
4.
Знайти екстремум функції
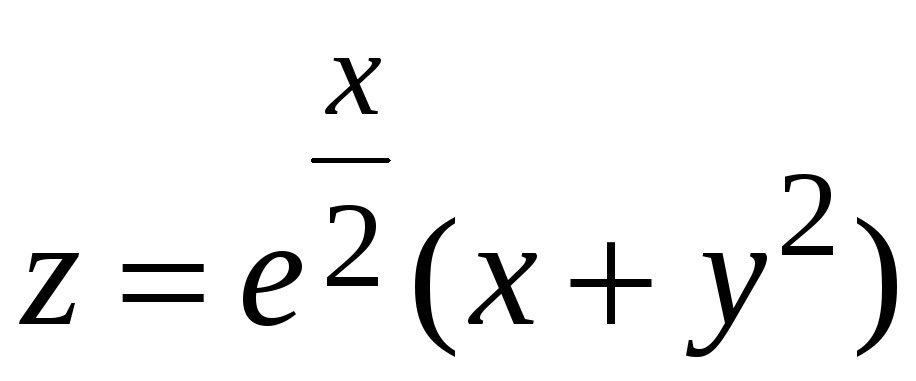 .
.
5.
Знайти розв’язок задачі Коші
 .
.
№ 29
1. Векторне поле. Потік векторного поля через просту і замкнену поверхню. Фізичний зміст потоку векторного поля.
2.
При заданій лінійній густині заряду
![]() знайти заряд, розподілений вздовж лінії
знайти заряд, розподілений вздовж лінії
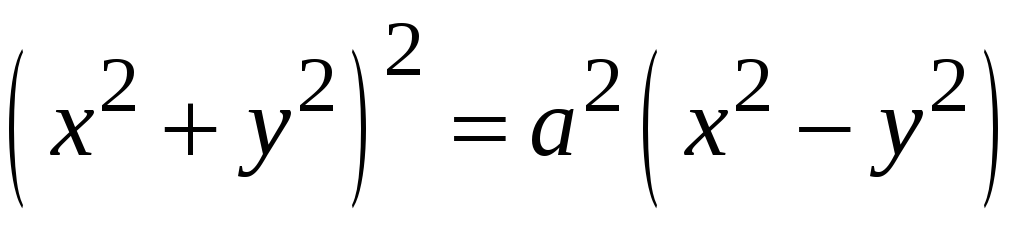 .
.
3.
Знайти
потік векторного поля
![]() через зовнішню сторону поверхні тіла,
обмеженого поверхнями
через зовнішню сторону поверхні тіла,
обмеженого поверхнями
![]() .
.
4.
Знайти
екстремум функції
![]() за умови
за умови
![]() .
.
5.
Знайти
розв’язок задачі Коші
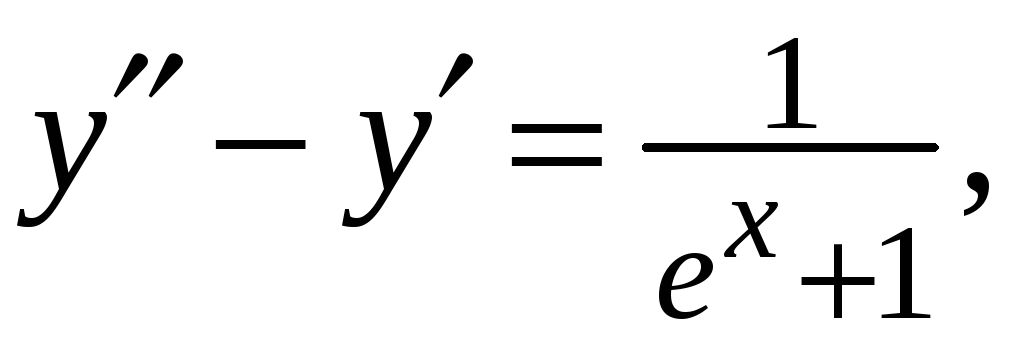
![]()
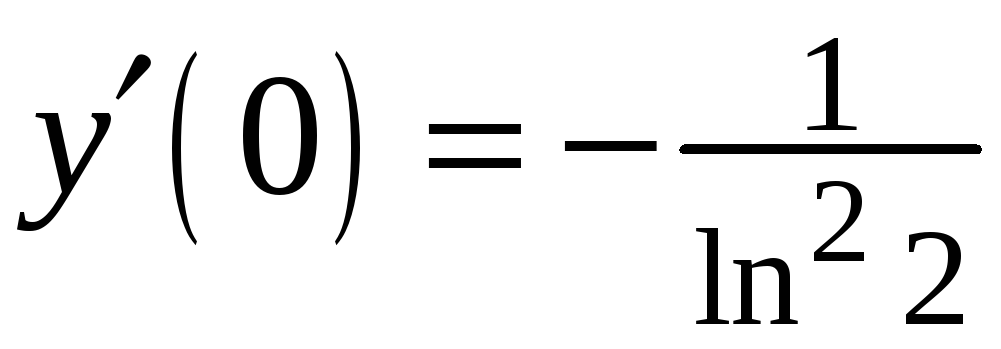 .
.
№ 30
1. Диференціальні рівняння вищих порядків, що допускають зниження порядку.
2.
Знайти роботу сили
![]() ,
яка виконується при переміщенні
матеріальної точки вздовж дуги
,
яка виконується при переміщенні
матеріальної точки вздовж дуги
![]() в напрямку зростання параметру.
в напрямку зростання параметру.
3.
Знайти масу частини поверхні
![]() ,
яка відтинається від неї поверхнями
,
яка відтинається від неї поверхнями
![]() ,
(І октант), якщо поверхнева густина маси
дорівнює
,
(І октант), якщо поверхнева густина маси
дорівнює
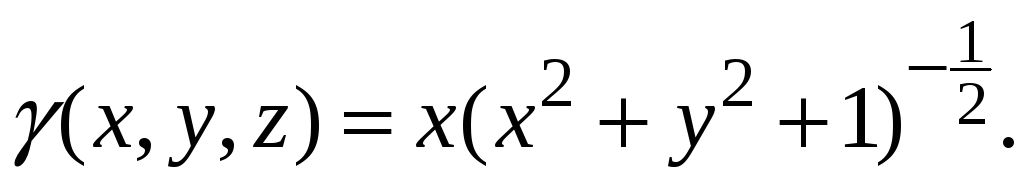
4.
Знайти екстремум функції
![]() .
.
5.
Зінтегрувати диференціальне рівняння:
 .
.
№ 31
1. Умови незалежності криволінійного інтегралу ІІ роду від форми кривої інтегрування.
2.
Знайти циркуляцію поля
![]() вздовж замкненого контуру С:
вздовж замкненого контуру С:
![]() ,
який обходиться проти годинникової
стрілки.
,
який обходиться проти годинникової
стрілки.
3.
Знайти
потік векторного поля
![]() через внутрішню сторону частини поверхні
через внутрішню сторону частини поверхні
 ,
яка розташована в першому октанті.
,
яка розташована в першому октанті.
4.
Знайти
екстремуми функції
![]() .
.
5.
Знайти
розв’язок задачі Коші
![]()
№ 32
1. Диференційовність функції багатьох змінних в точці. Поняття диференціалу в точці та його властивості. Наближені обчислення за допомогою диференціала.
2.
Показати, що поле
![]() потенціальне та знайти його потенціал.
потенціальне та знайти його потенціал.
3.
Знайти
потік векторного поля
![]() через зовнішню сторону поверхні тіла,
обмеженого поверхнями
через зовнішню сторону поверхні тіла,
обмеженого поверхнями
![]() .
.
4.
Знайти
екстремум функції
![]() за умови
за умови
![]() .
.
5.
Знайти
розв’язок задачі Коші
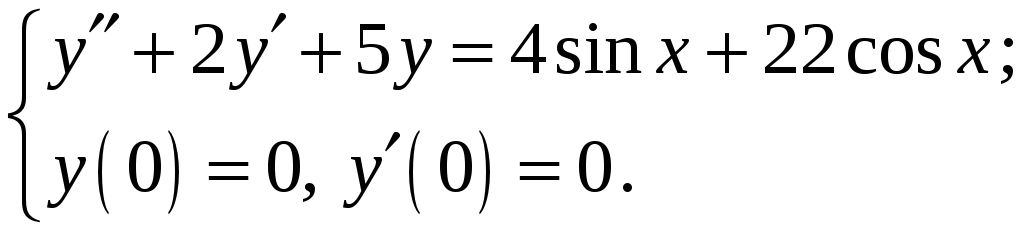
№ 33
1. Лінійні ДР першого порядку; рівняння Бернуллі.
2.
Показати,
що поле
![]() потенціальне та знайти його потенціал.
потенціальне та знайти його потенціал.
3.
Знайти
масу частини поверхні
![]() ,
яка відтинається від неї циліндром
,
яка відтинається від неї циліндром
![]() при заданій поверхневій густині маси
при заданій поверхневій густині маси
![]() .
.
4.
Знайти
найбільше та найменше значення функції
![]() в області
в області
![]()
5.
Знайти
розв’язок задачі Коші
![]()
![]()
№ 34
1. Векторне поле. Циркуляція та ротор векторного поля. Теорема Стокса про зв’язність між ними.
2.
Знайти масу кардіоїди
![]() ,
якщо лінійна густина маси
,
якщо лінійна густина маси
![]() .
.
3.
Знайти
потік векторного поля
![]() через зовнішню сторону поверхні тіла,
обмеженого поверхнями
через зовнішню сторону поверхні тіла,
обмеженого поверхнями
 .
.
4.
Знайти
екстремуми функції
![]() .
.
5.
Знайти
криву, для якої довжина відрізка, що
його нормаль відтинає від осі ОХ, дорівнює
![]() .
.
№ 35
-
ОЛДР n-го порядку. Властивості розв’язків ОЛДР n-го порядку та структура загального розв’язку ОЛДР n-го порядку.
-
Показати, що поле
 потенціальне та знайти роботу поля при
переміщенні матеріальної точки від
точки А(-1,2) до В(2,3).
потенціальне та знайти роботу поля при
переміщенні матеріальної точки від
точки А(-1,2) до В(2,3). -
Знайти масу частини однорідної поверхні
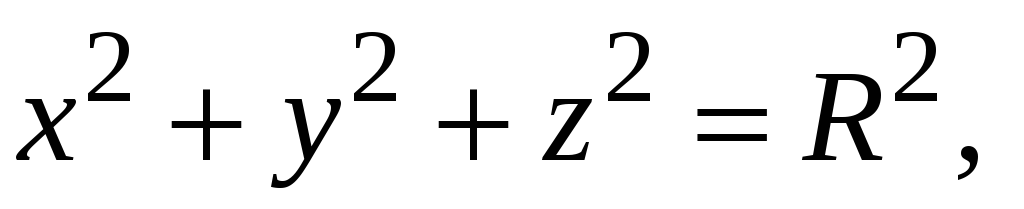 яка
відтинається від неї поверхнями
яка
відтинається від неї поверхнями
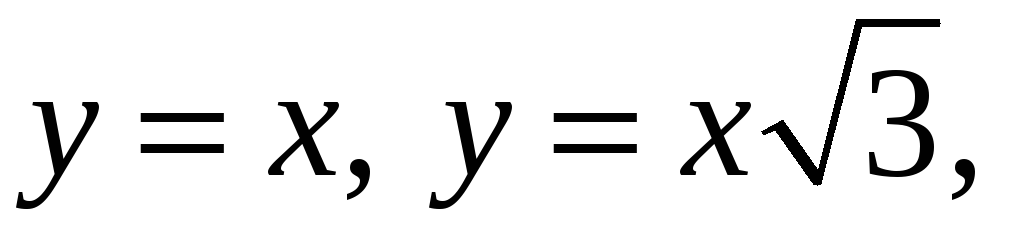
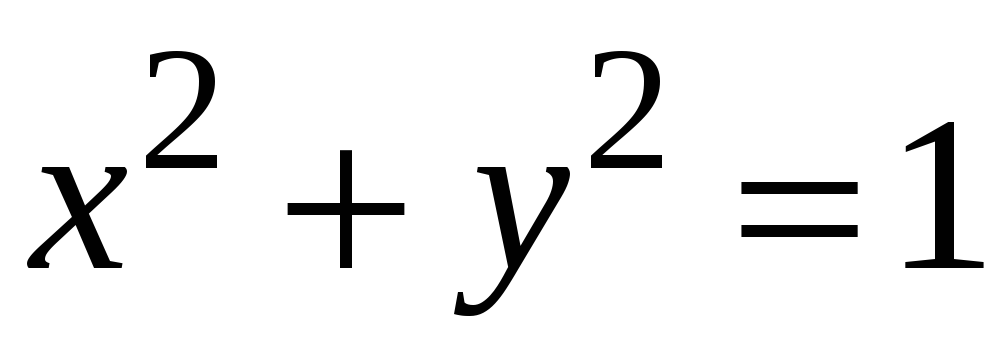 ,
,
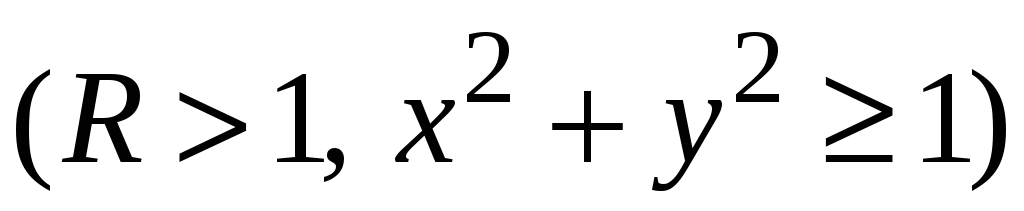 перший
октант.
перший
октант. -
Знайти екстремум функції
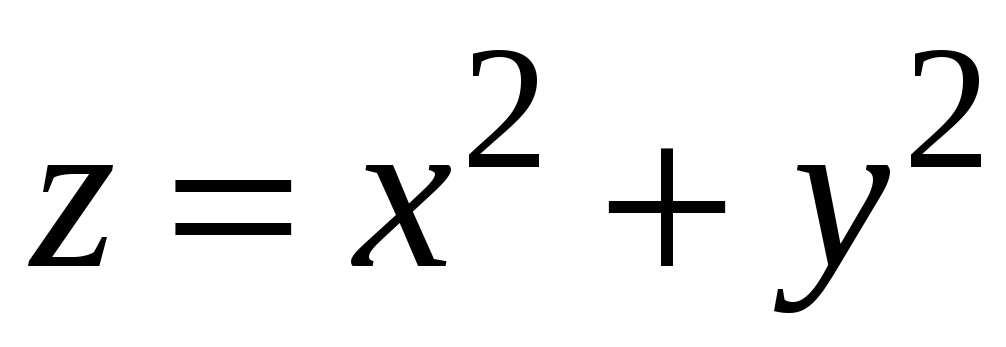 за умови
за умови
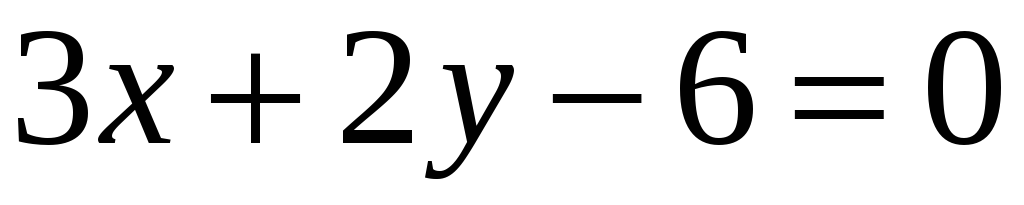 .
.
5.
Знайти
розв’язок задачі Коші

№ 36
-
Орієнтація поверхні. Поняття поверхневого інтегралу ІІ роду, правило обчислення по простій поверхні, зведення до подвійного, властивості, геометричний і фізичний зміст.
-
Знайти масу однієї арки циклоїди

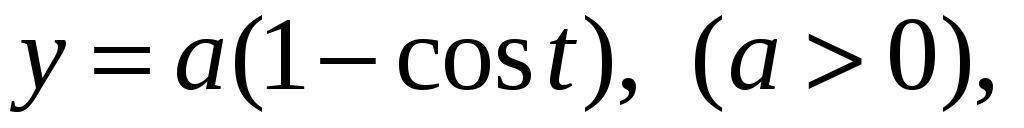 якщо
лінійна густина маси
якщо
лінійна густина маси
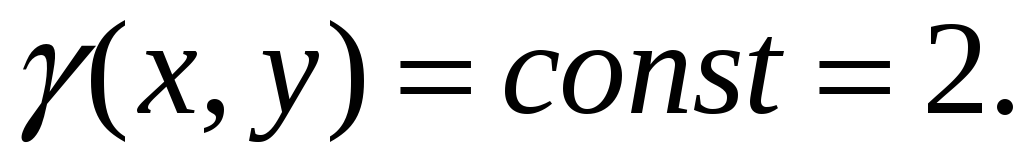
-
Знайти потік векторного поля
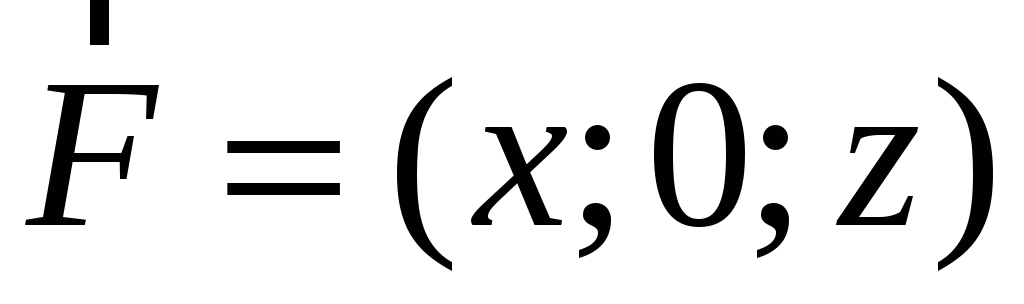 через зовнішню сторону поверхні тіла,
обмеженого поверхнями
через зовнішню сторону поверхні тіла,
обмеженого поверхнями
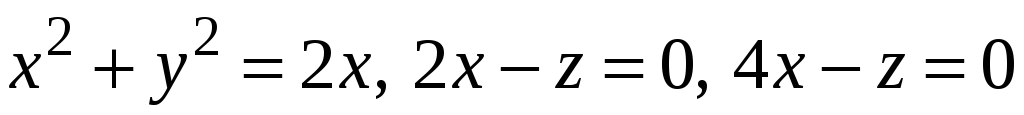 .
. -
Знайти площу фігури, обмеженої лініями
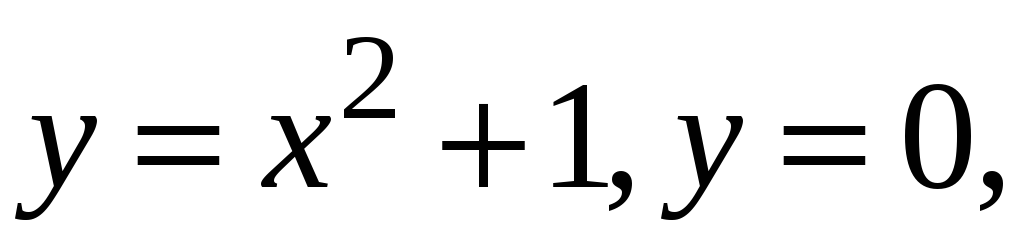

-
Знайти розв’язок задачі Коші
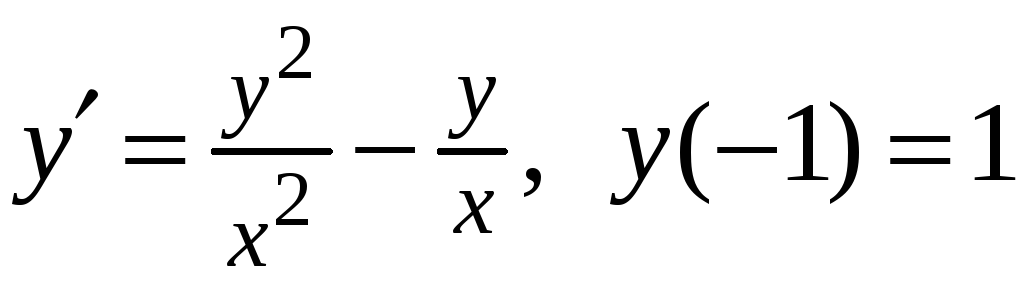 .
.
№ 37
-
Ротор векторного поля: означення, властивості, інваріантне означення, фізичний зміст. Формула Стокса в векторній формі.
-
Знайти масу заряду, розподіленого вздовж кривої
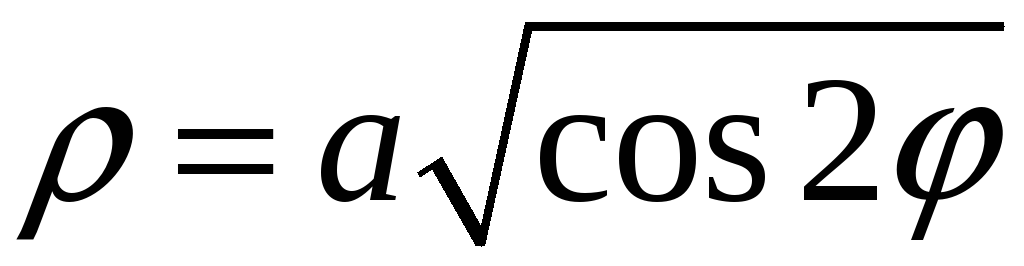 ,
якщо лінійна густина заряду
,
якщо лінійна густина заряду

-
Знайти потік векторного поля
 через зовнішню сторону поверхні тіла,
обмеженого поверхнями
через зовнішню сторону поверхні тіла,
обмеженого поверхнями
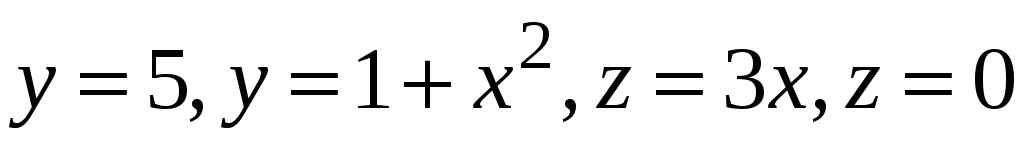 (І октант).
(І октант). -
Знайти екстремум функції
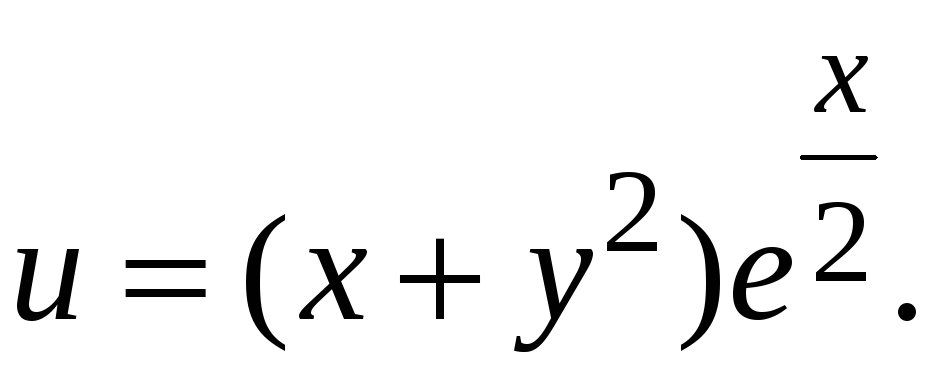
-
Знайти закон руху матеріальної точки, маса якої
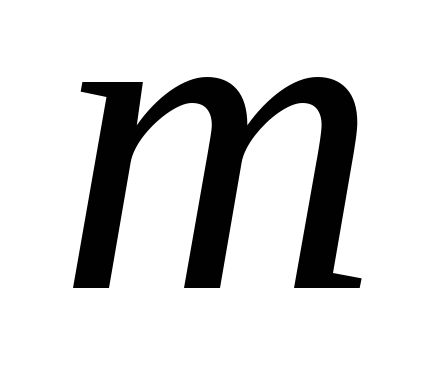 ,
по прямі ОА під дією відштовхуючої
сили, обернено пропорційної кутові
відстані х=ОМ від точки М до нерухомого
центру.
,
по прямі ОА під дією відштовхуючої
сили, обернено пропорційної кутові
відстані х=ОМ від точки М до нерухомого
центру.
№ 38
-
Означення ДР та його розв’язку. ДР 1-го порядку. Поле напрямів і ізоклін. Теорема Коші. Загальний розв’язок і розв’язок задачі Коші.
-
Знайти масу заряду, розподіленого вздовж дуги
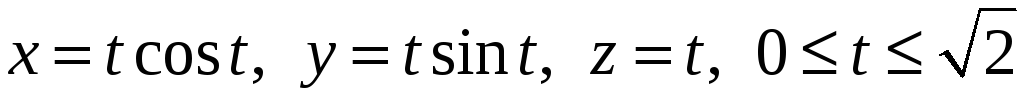 ,
якщо лінійна густину заряду
,
якщо лінійна густину заряду

-
Знайти потік векторного поля
 через
зовнішню сторону частини поверхні
через
зовнішню сторону частини поверхні
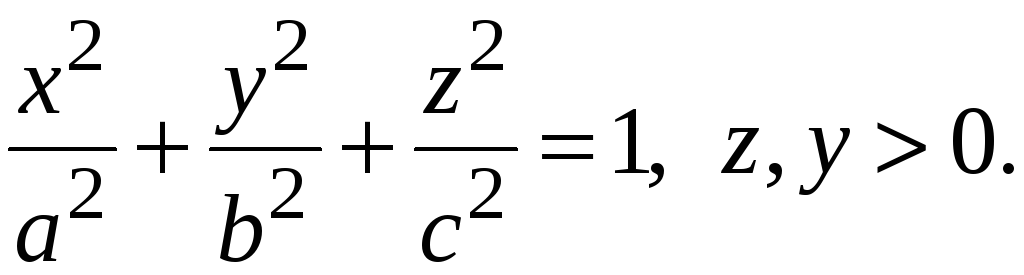
-
Знайти загальний розв’язок рівняння
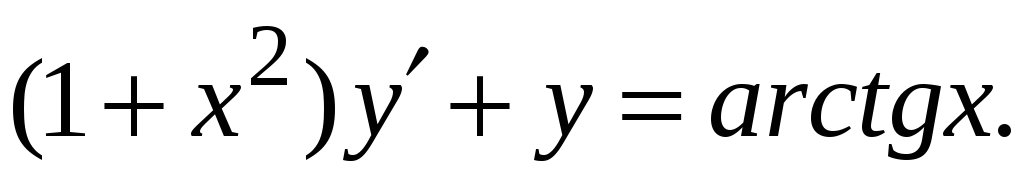
-
Знайти найбільше та найменше значення функції
 в області області D:
в області області D:
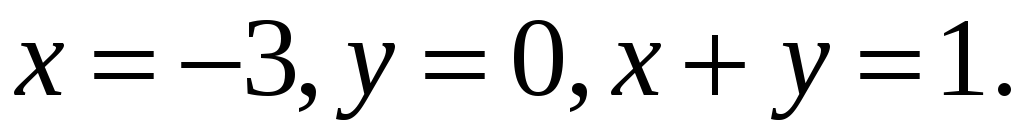
№ 39
