Лекція № розрахунок стиснутих стержнів на стійкість.

До числа задач курсу “Опір матеріалів” крім розрахунків на міцність та жорсткість відносяться також розрахунки на стійкість.

Розрахунок на стійкість необхідний для тих елементів, конструкції яких являють собою відносно довгі та вузькі стержні, тонкі пластинки та оболонки. Тут розглядаються лише найпростіші випадки розрахунку на стійкість стиснутих стержнів.

На стійкість обов’язково перевіряють всі стиснуті елементи каркасу котельного агрегату, які являють собою тонкі стержні прокатного профілю або набрані з прокатних профілів (рис. 10.1).

Тонкі колони трубчатої печі, опори та стояки наземних переходів трубопроводів, що закріплені фермами, кронштейни опорних пристроїв, що працюють на стиск і які набрані з прокатних профілів.(рис. 10-1).

Довгі труби втрачають стійкість при стисканні їх поздовжнім зусиллям як пружні стиснуті стержні.

1.Стійка та нестійка форма рівноваги.

При розрахунках на міцність, що розглядались у попередніх розділах, ми виходили з умови рівноваги елемента, конструкції або системи, і при цьому вважали, що стан рівноваги стійкий.

Під стійкоюформою рівноваги ми розуміємо таку, коли деформоване тіло при любому відхиленні від положення рівноваги намагається повернутися у початковий стан і повертається до нього після зняття зовнішнього навантаження (рис. 10.2, а).

При нестійкій формі рівноваги деформоване тіло, яке виведено зі стану рівноваги, не повертається у початковий стан, а має тенденцію продовжувати деформуватися у заданому напрямку.(рис. 10.2.б).

Розраховувати на міцність елемент, конструкції, який знаходиться у стані нестійкої рівноваги, не має ніякого сенсу, тому що елемент за будь-яких обставин вийде з такого стану, при цьому можуть з’явитися недопустимі деформації, що потягне за собою руйнування всієї конструкції.

Стійкий або нестійкий стан рівноваги пружного тіла залежить від його розмірів, матеріалу та величини і напрямку дії зовнішніх сил. Наприклад, система показана на (рис. 10.2,а) буде знаходитись в умовах стійкої рівноваги при малих значеннях зовнішнього навантаження Р, тобто до деякого граничного значенняР, перебільшення якого приведе за собою втрату стійкості початкової форми рівноваги. Це навантаження називають критичним(Ркр)

Очевидно, Ркр– це граничне руйнуюче навантаження, тому що форма рівноваги буде втрачена і руйнування неминуче. Причому руйнування від втрати стійкості небезпечне тим, що воно відбувається раптово; при низьких значеннях напружень, коли міцність конструкції не вичерпується.

Для забезпечення надійності необхідний деякий запас стійкості по відношенню до Ркр, тобто [P] = Pкр/n_ст , деn_ст– коефіцієнт запасу стійкості.

Початок дослідженням стійкості поклав Ейлер.

Розглянемо визначення Ркрпри стисканні тонкого довгого стержня у межах пружності.

2. Формула Ейлера для визначенняР_кр стиснутого стержня.

Покладемо, що при значенні Р≈Ркр(трошки більше) стержень з шарнірно закріпленими кінцями згубить стійкість (рис.10.3). При цьому будемо вважати, що силаР≈Р_крне викликає у стержні напружень, які перевищують границю пропорційності і величини прогину не великі, тобто: _кр ≤_пц.

Тоді для визначення прогину скористаємось наближеним диференціальним рівнянням пружної лінії:

У рівнянні I_min, тому що втрата стійкості відбувається відносно головної центральної (рис. 10.4) осі “min”, за напрямком другої головної центральної осі “max” (рис. 10.4).

Згинальний момент М(х) = -Рw, де в правій частині “ – “, тому що знак прогину протилежний знаку згинального моменту. Отримаємо:

Позначимо

Отримаємо однорідне лінійне диференціальне рівняння:

Його загальний розв’язок: . Сталі інтегруванняА та В знайдемо з граничних умов: при х = 0, W = 0 та при х = l , W = 0.

З першого В = 0, а з другого W=Asinkl=0 .

Якщо прийняти А = 0 , то W(x) = 0, що не задовольняє умові задачі, таким чином sinkl=0 , де kl=n, тобто n=1, 2, 3,……., або k²l²=²n²

Прирівняємо значення k²:

, звідки

Нас цікавить найменше значення сили Р, тобто Р_кр, при n = 1:

Рівняння зігнутої осі стержня:

Визначимо сталуА: , приw=w_max=f. Тоді , деn – число півхвиль синусоїди за довжиною зігнутого стержня (рис. 10.5). У випадку, що розглядається, тобто при шарнірному закріпленні кінців стержня, на його довжині укладається тільки одна півхвиля синусоїди (n=1).

Розглянемо інші випадки закріплення:

а) Стержень, закріплений з однієї сторони. Тутn =1/2, і 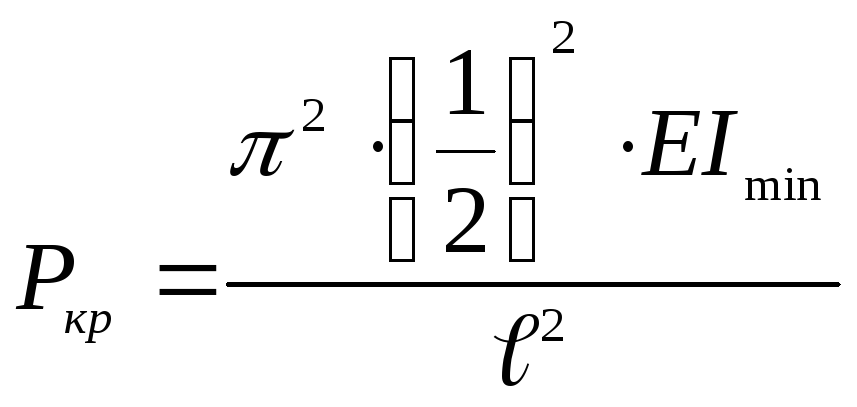, або, (рис. 10.6)

б) Стержень, жорстко закріплений з обох боків. У цьому випадку n= 2 і , або,

(рис. 10.7)

в) Стержень, жорстко закріплений з одного боку і шарнірно з іншого. Для нього:

n = 3/2 і , або, (рис. 10.8).

Очевидно, різні випадки закріплення стержня можна звести до основного, якщо ввести коефіцієнт приведеної довжини =1/n, і усі формули зведуться до однієї: ,

Ця формула носить назву, формули Ейлера. Значення для різних випадків закріплення стержнів. (рис. 10.9).

3. Межі застосування формули Ейлера .

Виведення формули Ейлера, засновано на застосуванні диференціального рівняння пружної лінії, яке справедливе у межах застосування закону Гука. Як наслідок, визначення Р_кр за формулою Ейлера можливе, якщо _кр _пц, тобто критичне напруження не перевищує границю пропорційності матеріалу. Визначимо _кр: ,

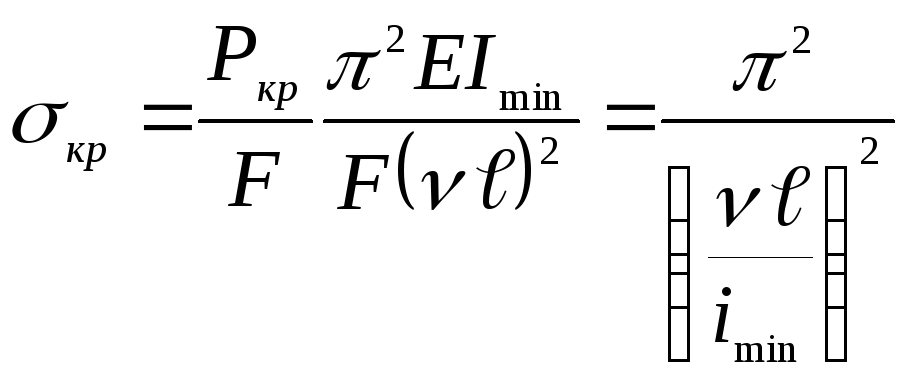Введемо поняття - гнучкість стержня. Вона залежить від його розмірів і способу закріплення. Одержимо,

звідки слідує що _кр залежить від матеріалу стержня і його гнучкості.

Покажемо цю залежність графічно для сталі 3 (рис. 10.10).

З графіка можна побачити що із збільшенням гнучкості _кр прямує до нуля. Очевидно існує якесь граничне значення гнучкості для стержня з певного матеріалу, для якого справедлива формула Ейлера. Тобто , звідки, і формула Ейлера може бути застосована, якщо≥_гр. При цьому, для значень <_гр , тобто при _кр>_пц, формула Ейлера дає завищені значення, тобто користуватись формулою небезпечно. Інженер – дослідник Ясинський одержав емпіричну формулу для визначення, _кр за границею пропорційності на основі дослідних даних:

_кр= a - b, - для пластичних матеріалів,

_кр= a - b+с² - для крихких матеріалів де a, b,с – емпіричні коефіцієнти.

4. Практичні розрахунки стиснених стержнів на стійкість.

При практичному розв’язку питання про підбір перерізу стиснутого стержня не можливо допустити виникнення у стержні критичного напруження – потрібно ввести деякі коефіцієнти запасу стійкості –n_ст, причому при поздовжньому згинанні коефіцієнт запасу для більшості матеріалів приймається більш високий, ніж при розрахунку на міцність, тому що стиснені стержні втрачають свою несучу здатність від втрати стійкості раніше, ніж від втрати міцності, тому що критичні напруження, завжди менші границі текучості, або границі міцності, тобто

_кр<_н, де

_н =  _т– для пластичних матеріалів;

_н =  _в – для крихких.

Таким чином, допустиме напруження при поздовжньому згинанні:

[]_ст=, де_кр визначається, якщо воно в межах пропорційності, за формулою Ейлера, якщо воно вище _пц – наприклад, за формулою Ясинського.

Приблизно можна приймати наступні значення n_ст:

Сталь: 1,8÷3,0;

Чавун: 5,0÷5,5;

Дерево: 2,8÷3,2.

Але допустиме напруження на стійкість та допустиме напруження на міцність, взаємно пов’язані. Виразимо []_ст через []:

, звідки

.

Позначимо: , тоді []_ст=[] ^. .

Назвемо  - коефіцієнтом зниження основного допустимого напруження. Цей коефіцієнт підраховано для значень гнучкості, від 0 до 200 для основних конструкційних матеріалів, його значення в залежності від матеріалу і гнучкості  приводяться у довідникових таблицях.

Тепер можна записати умову стійкості:

 =Р/F  []_ст, або

 =P/F [] ^. ., де

дійсне напруження  визначається як при простому стискуванні, але допустиме напруження знижується з врахуванням гнучкості стержня:

[]_ст =[] ^. .

Як формула Ейлера, так і метод розрахунків за коефіцієнтом  дозволяють виконувати три види розрахунків – перевірочний, проектувальний та визначення вантажопідйомності.

Відмітимо, що проектувальний розрахунок за коефіцієнтом  можна виконати тільки методом послідовного наближення, задаючись значеннями  та наближаючи їх один до одного, тобто в умові стійкості дві невідомі величини – площа F та коефіцієнт . Нижче представлені приклади різних видів розрахунків за обома методами.

5. Раціональна форма та раціональне розташування переріза.

При розрахунку стержня на стійкість потрібно намагатися, щоб стержень був рівно-стійкий в усіх напрямках. Якщо в обох головних площинах приведена довжинаоднакова, то раціональний переріз-коло, кільце або квадрат, тобто переріз, у якогоi_z=i_yабоI_z=I_y(рис. 10.11)

Якщо приведена довжина() у різних площинах не однакова, то переріз не повинен мати однакові i_z і i_y, а розташовувати його потрібно так, щоб _max при цьому знизилась, тобто була спрямована до однакових значень , аби стержень став рівно-стійким. Так для стержня представленого на рис. 10.12 гнучкість в головних площинах:

_xoz=_y=2 ^. l/i_y ; _xoy=_z=1 ^. l/i_z.

Переріз повинен мати таку форму і так бути розташований, щоб

i_y <i_z k, тобто необхідно знизити максимальну гнучкість.

Ряд таких перерізів показано на рис. 10.13. Це перш за все перерізи, які набрані з прокатних профілів.

Приклади розрахунків на стійкість.

В залежності від постановки задачі є три види розрахунків на стійкість: перевірочний, визначення допустимих навантажень та проектувальний - визначення розмірів поперечного перерізу стержня. Всі ці розрахунки можна проводити одним з методів – за формулою Ейлера (обов’язково виконуючи умови її застосування, тобто ≥ _пр) або за коефіцієнтом зниження допустимого напруження.

1. Перевірити на стійкість стиснуту сталеву стійку трубчатого перерізу з _пц=540 МПа, Е = 2,15 10⁵ МПа, потрібний коефіцієнт запасу стійкості n_у = 3,5 (рис. 10.14).

Розв’язок.

Для використання формули Ейлера визначимо граничну гнучкість і гнучкість стояка. Гранична гнучкість матеріалу стояка:

. Для визначення гнучкості стояка знайдемо його момент інерції та радіус інерції.

Моменти інерції стояка всі однакові:

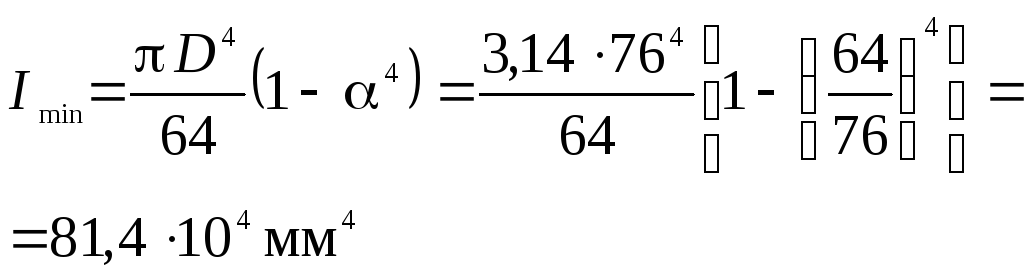
Площа перерізу

.

Радіус інерції

Гнучкість стояка при =0,7:

Тому що ≥_гр, за формулою Ейлера визначимо критичну силу:. Дійсний коефіцієнт запасу стійкості:що, трошки більше потрібного, тобто стійкість конструкції забезпечена.

Лекція №

Тема: «Розрахунки при ударних навантаженнях»

Явище удару має місце тоді, коли швидкість розглядуваного елемента конструкції або стичних з ним частин протягом дуже малого проміжку часу змінюється на скінченну величину.

Розглянемо 2 випадки:

1. Вантаж прикладається до стрижня статично, тобто навантаження наростає від нуля до максимального значення і стискає стрижень на величину .

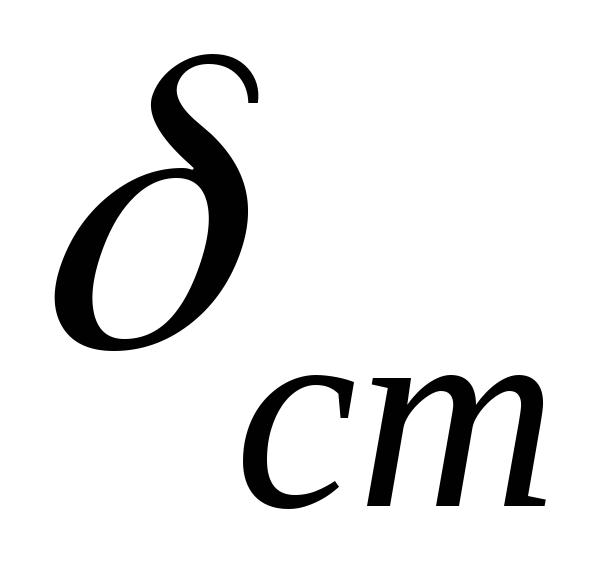2. Вантаж падає з висоти Н і ударяючи по стрижню спричинює у ньому стиск.

Зміна деформацій та переміщень при ударній дії навантаження Q порівняно з переміщеннями (деформаціями) при статичній дії того самого навантаження характеризується коефіцієнтом динамічності:

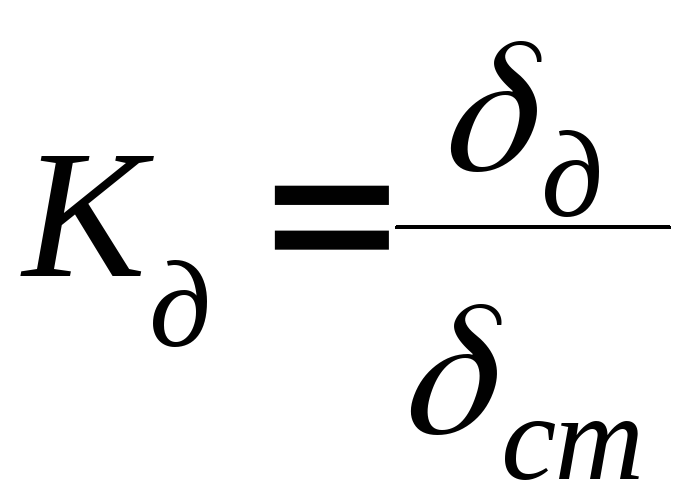
Звідки, .

Враховуючи лінійний зв'язок між напруженнями та деформаціями, а також припускаючи, що модулі пружності при статичній і ударній дії навантаження однакові, можна записати:

, де

Переміщення будуть дорівнювати:

, де - жорсткість;

; - статичне навантаження, що дорівнює вазі падаючого вантажу ()

- динамічне навантаження, що являє собою силу інерції тіла, яке ударяє, в перший момент його зіткнення зі стержнем.

Зміна кінетичної енергії падаючого вантажу чисельно дорівнює роботі вантажу при його падінні та деформуванні стержня:

Потенціальна енергія деформації тіла при ударі дорівнює:

Користуючись законом збереження енергії:

Тоді

і враховуючи, що , можна записати:

Знак «-» треба відкинути, так як знак динамічної деформації не може бути протилежним знаку статичної:

Враховуючи , отримаємо:

Враховуючи, що , деV – швидкість падаючого вантажу в момент початку удару, тоді коефіцієнт динамічності можна записати:

Ураховуючи, що ,

, де - кінетична енергія падаючого вантажу в момент початку удару;

- потенціальна енергія деформації стержня, при статичній дії сили, яка дорівнює вазі ударного вантажу , тобто:

; ;, де“” – жорсткість.

Оскільки висота падіння вантажу , то під коренем при визначенніодиницею нехтують, тобто:

, але це наближена формула.

Напруження при ударі визначається, як:

, - статичне напруження.

Зусилля при ударі:

, - статичне зусилля.

Умова міцності при ударі має вигляд:

Коефіцієнт запасу міцності можна вибрати таким, як і при статичному навантаженні (1,41,6), оскільки динамічність вже відображена у розрахункових формулах коефіцієнтом. Однак, враховуючи наближеність розглянутого методу розрахунку, цей коефіцієнт беруть більшим ().