Лекція № Складний опір

Під складним опором розуміють різні комбінації раніше розглянутих простих видів навантаження (розтягу-стиску, зсуву, кручення та згину).

При аналізі складного опору справедливі принцип суперпозиції, принцип незалежності дії сил.

Складний та косий згини

Складний згин спричиняється силами або моментами, розташованими в різних площинах, які проходять крізь вісь балки. Такий згин зветься також неплоским згином, оскільки зігнута вісь балки не є плоскою кривою.

1 та 2— силові площини.

Якщо всі навантаження, що спричиняють згин, діють в одній площині, що не збігається ні з однією з головних площин, то згинання зветься косим.

Як у випадку неплоского, так і у випадку косого згину, найзручніше зводити згини до двох плоских.

Обчислимо напруження в деякій точці (y,z) довільного поперечного перерізу, розмістивши її для певності в першому квадранті. Напрями головних осей показані на рисунку. Згинальні моменти будемо вважати додатними, якщо вони спричинюють у точках першого квадранта розтягуюче напруження.

Виходячи з принципу суперпозиції, знайдемо напруження в зазначеній точці, розглядаючи два плоских згини.

;

(1)

Нормальні напруження при складному згині.

У випадку косого згину

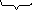
(2)

Рівняння нейтральної лінії при складному згині в будь-якому поперечному перерізі дістанемо з формули (1), поклавши

(3)

y₀, z₀ —координати точок нейтральної лінії.

­­– рівняння прямої, що проходить крізь початок координат (центр ваги перерізу).

Положення нейтральної лінії характеризується її кутовим коефіцієнтом: (4)

У формулі (4), кут вважається додатним, якщо відраховується від осі Z проти годинникової стрілки. Для моментів, у формулі (4), знаки моментів такі, як за правилом І квадранта.

Якщо у деякому перерізі бруса, де діють найбільші згинальні моменти треба знайти положення нейтральної лінії, то зручно спочатку показати положення силової лінії Р-Р.

Нейтральна лінія не перпендикулярна силовій площині, перпендикулярна тільки вектору моменту.

– кут нахилу силової площини.

Тоді після находження положення нейтральної лінії будуємо епюру напружень та визначаємо положення небезпечних точок А і В.

Умова міцності для небезпечних точок:

Момент вважається додатнім, якщо він викликає розтяг у першому квадранті

У загальному вигляді неплоского згину умова згину має вигляд:

Розглянемо балку:

;

Прогин за віссю Y:

Прогин за віссю Z:

Повний прогин:

Складний згин балки круглого перерізу:

;

відкладаємо за годинниковою стрілкою, тобто від осі Z. Тоді нейтральна лінія проходить через вектор моменту М.

Умова міцності:

Порядок розрахунку:

1. Визначаємо положення небезпечної точки по довжині балки.

2. У знайденої небезпечної точки розглядаємо переріз балки і визначаємо небезпечні точки в перерізі.

Згин з розтягом (стиском)

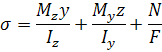
Для визначення положення нейтральної лінії:

Рівняння прямої, що не проходить через початок координат.

;

;

Умова міцності:

Якщо переріз симетричний:

Для круглого проділу:

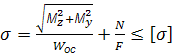
Позацентровий розтяг (стиск) прямого бруса

Позацентровий розтяг (стиск) є окремим випадком складного згину з розтягом (стиском), при якому брус розтягується силами паралельними осі бруса, так що рівнодіюча їх не збігається з віссю бруса, а проходить крізь точку Р, що називається полюсом сили.

N=P; ;

=

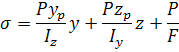
= ; – радіуси інерції.

Рівняння нейтральної лінії:

Відрізки, що відсікаються нейтральною лінією

; ;

0 ; ;

==

==

Для прямокутного перерізу:

Можна визначити зону таких віддалень сили Р від осі, при яких нормальні напруження по всьому поперечному перерізу будуть одного знака. Така зона називається перерізом ядра. Це важливо для брусів з матеріалів, що погано чинять опір розтягу (наприклад для цегляної кладки, бетону та сірого чавуну).

Отже, ядром перерізу називають зону навколо центра ваги поперечного перерізу, яка має таку властивість: якщо позацентрово-прикладене навантаження розташоване в зоні ядра, то нормальні напруження в усіх точках поперечного перерізу мають один знак.