8. Потенціальне, соленоідальне і гармонічне векторні поля
Розглянемо векторне поле
(8.1)
задане
в деякій просторовій області
,
.
Означення
1.
Векторне поле (8.1) називається потенціальним,
якщо існує неперервно диференційовна
скалярна функція
,
,
така що
.
(8.2)
Тотожність (8.2) означає, що одночасно виконуються три тотожності
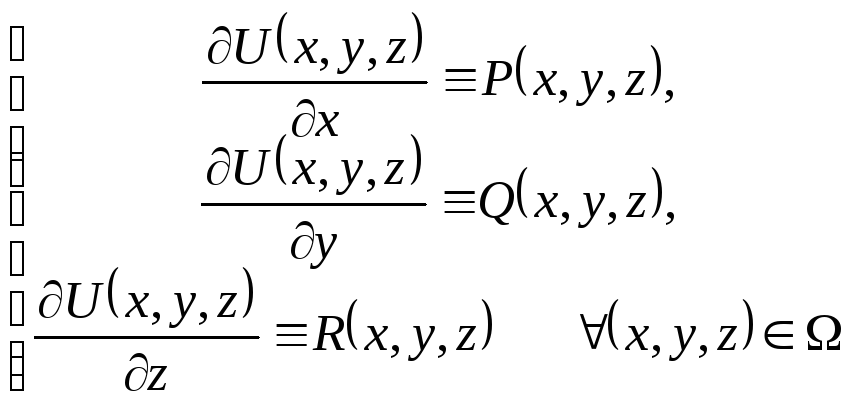(8.3)
При
цьому скалярну функцію
називають
потенціалом
векторного поля (8.1). Відоме наступне
твердження.
Теорема.
Для
того, щоб векторне поле (8.1) було
потенціальним
в області
,
необхідно і досить виконання тотожності
.
(8.4)
Оскільки
.
То тотожність (8.4) еквівалентна одночасному виконанню трьох тотожностей
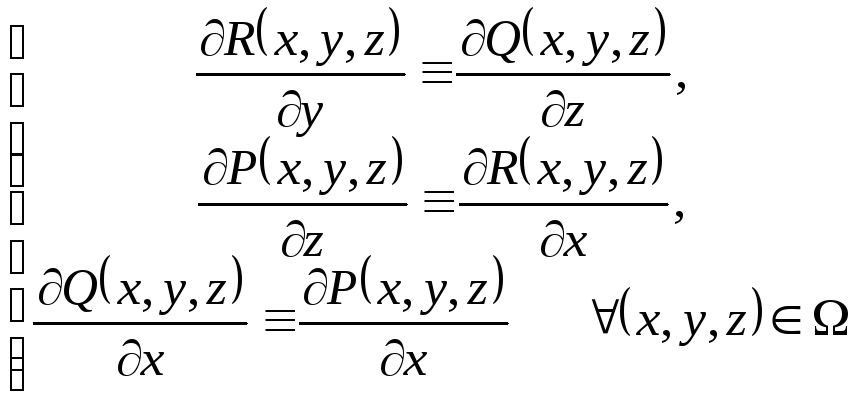(8.5)
Зауваження. У випадку, коли векторне поле (8.1) є потенціальним криволінійний інтеграл
не
залежить від кривої, яка з’єднує точки
і
, а залежить тільки від початкової і
кінцевої точок
,
.
При цьому інтеграл можна обчислити за
наступною формулою
Наслідок.Якщо
поле (8.1) є потенціальним, то відповідний
криволінійний інтеграл по замкнутому
контуру
дорівнює нулю:
.
Приклад. Переконатись, що векторне поле
є
потенціальним і знайти потенціал
.
Розв’язування. Обчислюємо ротор цього поля, маємо
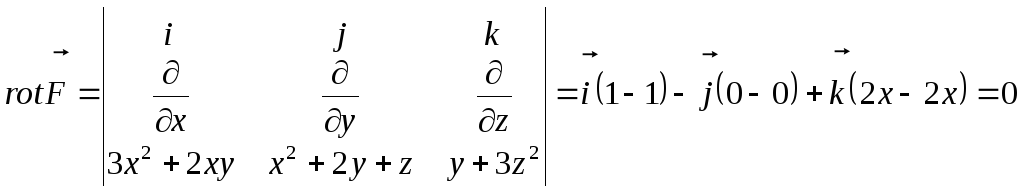
Отже
поле є потенціальним і диференціал
функції
має вигляд
.
Для
знаходження функції
маємо
систему рівнянь
З
першого рівняння отримуємо
,
де
-невідома
функція.
Підставляючи
в друге рівняння, отримуємо
,
тобто
,
звідси випливає
.
Далі отримуємо
.
Підставимо в третє рівняння
,
-довільна
стала.
Остаточно маємо потенціал даного поля
.
Означення
2.
Векторне поле (8.1) називається
соленоїдальним,
якщо в усіх точках
виконується рівність
.
(8.6)
З формули Гауса-Остроградського випливає, потік соленоїдального поля через довільну замкнену поверхню, що знаходиться в деякій однозв’язній області, дорівнює нулеві.
Слово „соленоїдальне” у перекладі з грецької мови означає „трубчасте”, бо для таких полів справедливий закон збереження інтенсивності векторної трубки.
В гідродинаміці соленоїдальне поле-це поле без джерел, у якому через кожен переріз векторної трубки протікає одна й та сама кількість рідини. В електростатиці це поле без зарядів.
Відоме наступне твердження.
Теорема.
Для
того, щоб векторне поле (8.1) було
соленоїдальним
в області
,
необхідно і досить, щоб існував такий
вектор
,
(8.7)
для
якого в усіх точках
виконується тотожність
(8.8)
Тотожність (8.8) можна записувати у координатній формі:
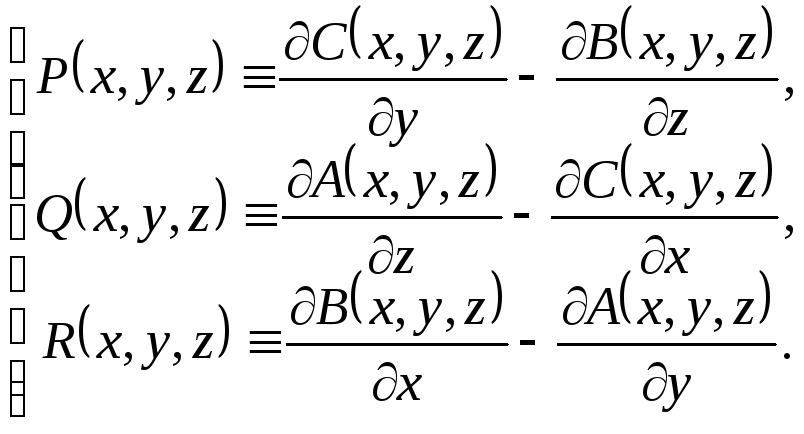(8.9)
Вектор (8.7) називають векторним потенціалом поля (8.1).
Зауваження.
Якщо
існує один вектор (8.7), що задовольняє
тотожності (8.8), то і будь-який вектор
,
при довільній неперервно диференційовній
скалярній функції
,
також буде задовольняти тотожність
(8.8).
Отже, векторні потенціали соленоїдального поля відрізняються один від одного на градієнт довільного скалярного поля.
Приклад.
Знайти
векторний потенціал
соленоїдального векторного поля
.
Розв’язування. Із тотожностей (8.9) отримуємо систему диференціальних рівнянь
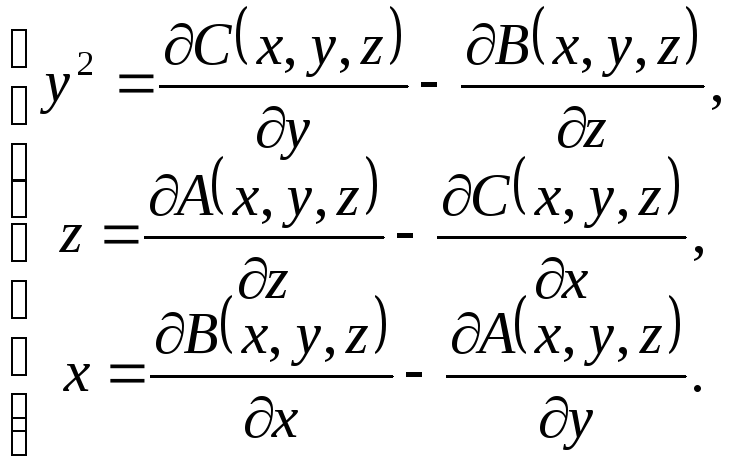(8.10)
Оскільки
векторний потенціал визначається
неоднозначно:
,
то
можна припускати, що
.
Система (8.10) запишеться в наступному
вигляді
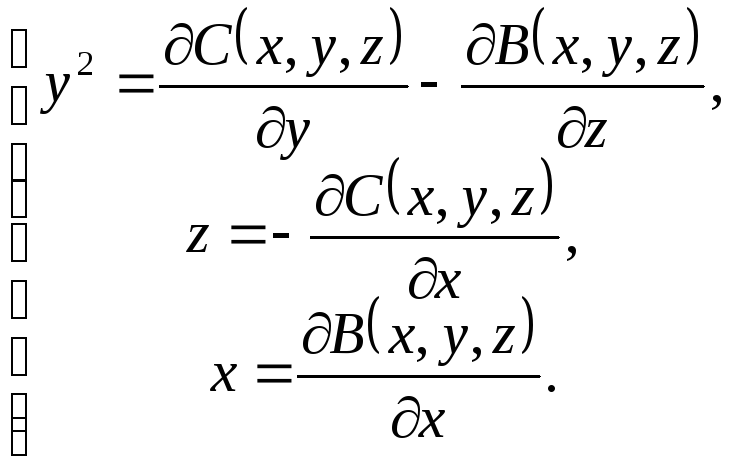
Із
посліднього рівняння вибираємо
.
Тоді із першого і другого рівнянь
отримуємо
.
Таким чином, один з векторних потенціалів
має вигляд
.
Означення
3.
Векторне поле (8.1) називається гармонічним,
якщо в усіх точках
воно є одночасно
і потенціальним і соленоїдальним, тобто
в усіх точках
виконуються умови
.
З
першої умови випливає існування скалярної
функції
,
що
.
З
другої умови
,
де
-оператор
Лапласа. Отже, в гармонічному полі маємо
.
Це рівняння називається рівнянням Лапласа, а його розв’язки – гармонічними функціями.
Гармонічне поле ще означають як потенціальне, потенціалом якого є гармонічна функція. Прикладами гармонічних функцій є наступні
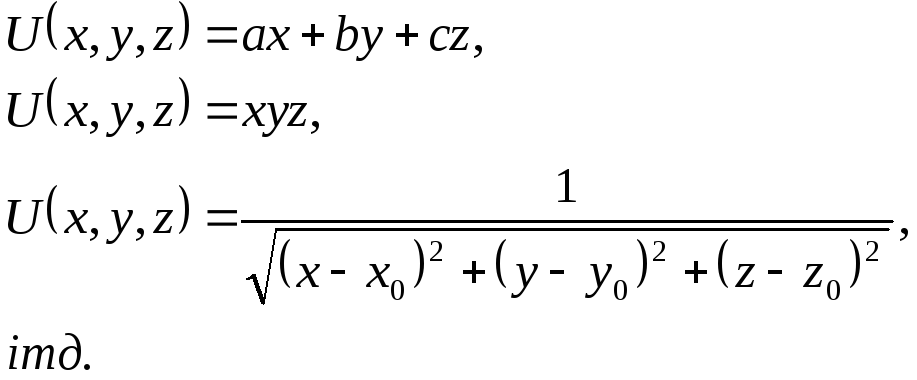
Довільне
векторне поле
завжди можна подати у вигляді суми
,
де
- потенціальне поле,
-соленоїдальне
поле.
Приклади для самостійного завдання
Вияснити,
чи буде векторне поле
соленоїдальним.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Вияснити,
чи буде векторне поле
потенціальним, якщо так, то знайти
потенціал.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
Вияснити,
чи буде векторне поле
гармонічним.
26.
27.
28.
29.
30.
