І.Поверхневі інтеграли

1.1. Поверхневі інтеграли першого роду.

Поверхневі інтеграли 1-го роду застосовуються при обчисленні площі деякої обмеженої, чи, можливо, деякої і необмеженої поверхні , маси цього кусочка поверхні при заданій густині маси, координат центра ваги поверхні, моментів інерції поверхні з розподіленою густиною маси.

Ми будемо розглядати поверхні в просторі , це придає цій теорії наглядність і певну її красоту, що викликає бажання студентів до вивчення цієї теорії.

Нехай в просторі задана частина деякої обмеженої поверхні

(1.1)

і в кожній точці цієї поверхні задана деяка функція. Поділимо поверхнюначастині виберемо на кожному з цих кусочків поверхні довільну точкуз координатами. Складемо наступну суму

, (1.2)

де - площа кусочка поверхні. Позначимо черезнайбільший із діаметрівкусочка поверхні.

Означення. Якщо існує скінчена границя сум (1.2) при незалежна від вибору точок, то цю границю прийнято називати поверхневим інтегралом першого роду по поверхніі записувати в наступному вигляді

. (1.3)

Основні властивості поверхневого інтегралу 1-го роду.

1.Нехай дві функції і є неперервними на , тоді для будь –

яких дійсних чисел виконується рівність

(1.4)

2.Якщо поверхня складена з двох поверхоньі,,

і при цьому поверхні, не мають спільних внутрішніх точок, то

. (1.5)

3.Якщо , то, де- площа поверхні.

4.Має місце нерівність

, (1.6)

де , - площа поверхні.

5. Якщо функція є неперервною на замкнутій поверхніто на

цій поверхні існує точка така, що

, (1.7)

де - площа поверхні.

Обчислення поверхневих інтегралів 1-го роду.

Нехай поверхню , яка визначається в неявному вигляді (1) можна записати в явному вигляді .При цьому змінюються в області ;- проекція поверхні на площину . Припускаємо, що функції є неперервними в області, функція є неперервною на поверхні .

Внаслідок розбиття поверхні на частини ,область розіб’ється на частини , які є відповідними проекціями частин на площину.Якщо позначити площу частини,то можна записати зв'язок між площами і : , - кут між нормаллю до поверхні в точці і віссю . Враховуючи рівність

,

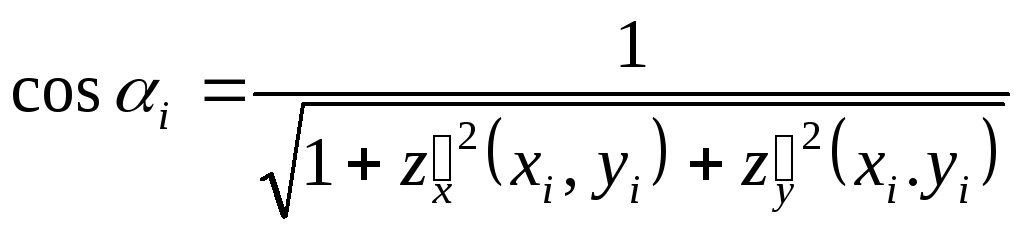інтегральну суму (2) запишемо у наступному вигляді

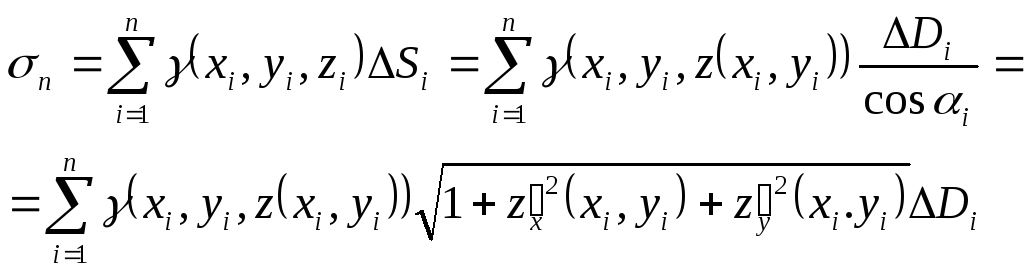
Звідси випливає зв'язок між поверхневим інтегралом 1-го роду і подвійним інтегралом:

. (1.8)

Якщо із неявного запису (1) поверхню можливо записати, тоді

. (1.9)

У випадку запису поверхні у виглядібудемо мати

. (1.10)

Нехай тепер поверхня записується в параметричному вигляді

(1.11)

В цьому випадку елемент площі записується в наступному вигляді ,

де

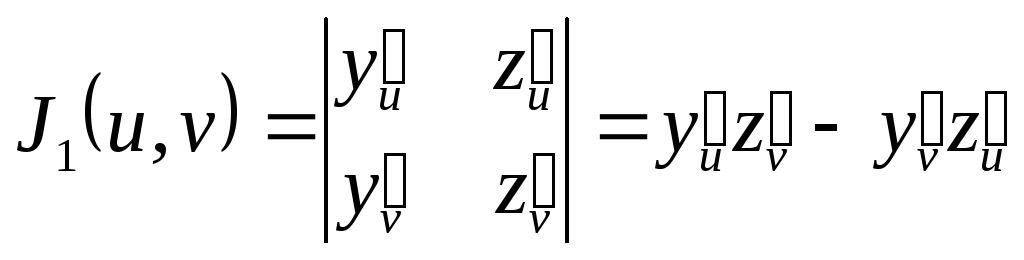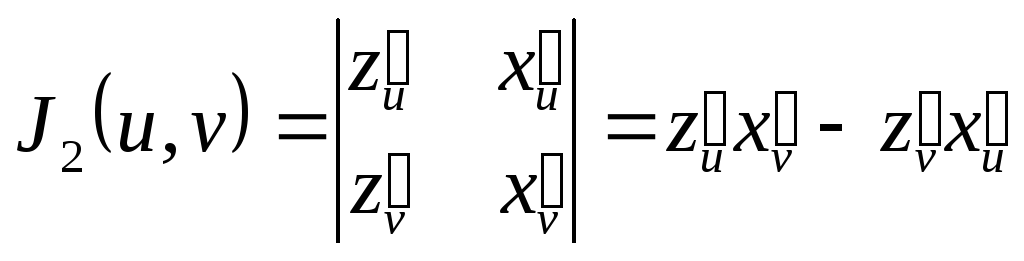, , (1.12) .

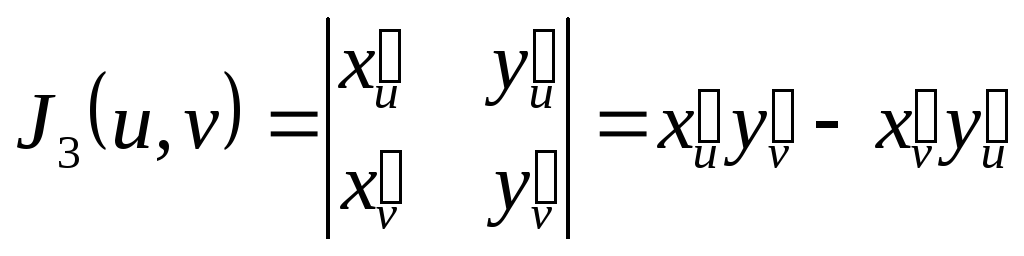Таким чином, поверхневий інтеграл (1.3) у випадку параметричного вигляду (1.11) поверх ні , обчислюється наступним чином

(1.13)

Приклад 1. Обчислити поверхневий інтеграл

,

де - частина площини, розміщена у першому октанті.

Рівняння заданої поверхні запишемо у вигляді, звідси отримуємо . Проекцією поверхні на площину є трикутник обмежений прямими . Тепер записаний поверхневий інтеграл зводим до подвійного і обчислюємо його.

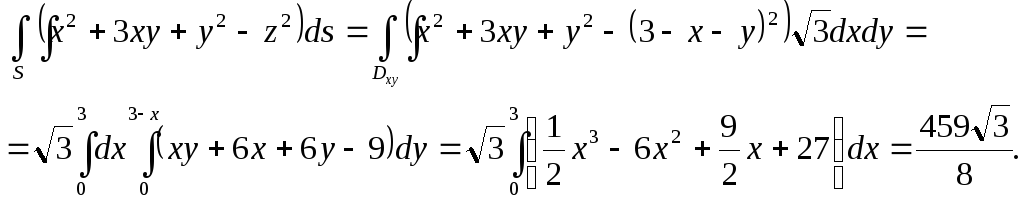
Приклад 2. Обчислити поверхневий інтеграл

,

де - повна поверхня сфера.

Поверхню запишемо в параметричному вигляді

При цьому параметри змінюються в границях

.

Підраховуємо якобіани (1.12), маємо

,

,

.

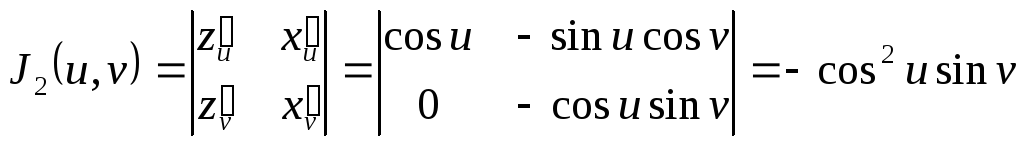Таким чином, отримуємо

і обчислюємо наш інтеграл

.

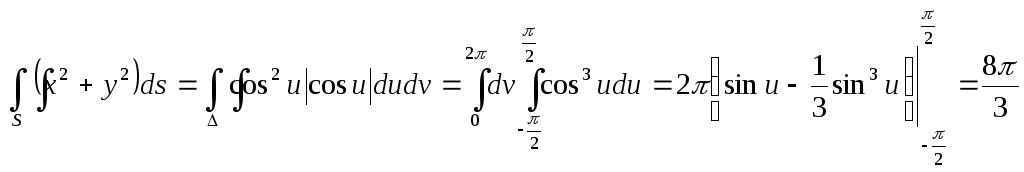Приклад 3. Обчислити поверхневий інтеграл

,

де - частина поверхні гелікоїда .

Записуючи похідні, ,,отримуємо

,

.

Таким чином, враховуючи формулу (1.13), маємо

.

Приклади для самостійного завдання

Обчислити поверхневий інтеграл першого роду по поверхні , де- частина площини, яка відсікається координатними площинами.

1.. (Відповідь:). 2.. (Відповідь:).

3.. (Відповідь:).

4.. (Відповідь:).

5.. (Відповідь:).

6.. (Відповідь:).

7.. (Відповідь:).

8.. (Відповідь:).

9.. (Відповідь:).

10.. (Відповідь:).

11.. (Відповідь:).

12.. (Відповідь:).

13.. (Відповідь:).

14.. (Відповідь:).

15.. (Відповідь:).

16.. (Відповідь:). 17.. (Відповідь:).

18.. (Відповідь:).

19.. (Відповідь:).

20.. (Відповідь:).

21.. (Відповідь:).

22.. (Відповідь:).

23.. (Відповідь:).

24.. (Відповідь:).

25.. (Відповідь:).

26.. (Відповідь:).

27.. (Відповідь:).

28.. (Відповідь:).

29.. (Відповідь:).

30.. (Відповідь:).

2.1. Поверхневі інтеграли другого роду.

Поверхневий інтеграл першого роду не залежить від орієнтації поверхні, оскільки площа куска поверхні, яка входить у інтегральну суму (1.2) є завжди додатною. Існує ряд важливих задач (наприклад про величину потоку рідини через задану поверхню за одиницю часу та ін.), в яких орієнтація поверхні відіграє важливу роль. Такі задачі приводять до поняття поверхневого інтегралу 2-го роду.

Нагадаємо означення двосторонньої поверхні і односторонньої. Розглянемо деяку гладку поверхню і на ній замкнений контур, який не має спільних точок з межею цієї поверхні. У довільній точціконтурупроведемо одиничний ортогональний вектордо поверхні. Переміщаємо точкуразом з нормаллювздовж замкнутого контуру. Повернувшись в початкову точку, ми можемо отримати той самий вектор, а можемо отримати протилежний вектор.

Означення 1.Гладка поверхня називається двосторонньою, якщо при обході вздовж будь-якого замкнутого контуру , який належить поверхні і не має спільних точок з краями поверхні, напрям нормалі до поверхні не

змінюється. Якщо ж на поверхнііснує замкнутий контур , при обході вздовж якого напрям нормалі змінюється на протилежний, то поверхня називаєтьсяодносторонньою.

Прикладом двосторонніх поверхонь є площина, конус, еліпсоїд і т.д. Прикладом односторонньої поверхні є листок Мебіуса.

На двосторонній поверхні вибір напряму нормалі в одній точці однозначно визначає напрям нормалі в усіх точках даної сторони поверхні.

Означення 2.Сукупність усіх точок поверхні із вказаним напрямом нормалі називається стороною поверхні, а вибір певної її сторони-орієнтацією поверхні.

Якщо поверхня визначена в неявному вигляді, то вектор

є ортогональним до поверхні . Часто векторназивають градієнтом і коротко записують

.

Нормуючи вектор , отримуємо одиничний вектор, ортогональний до поверхні.

При цьому , ,

прийнято називати направляючими косинусами нормального вектора до поверхні . По цих косинусах визначається сторона поверхні. Наприклад, якщо поверхнявизначається у явному вигляді, то можна покластиі направляючі косинуси ортогонального вектора записуються у вигляді

, , . (2.1)

Оскільки , то кут між віссюі нормальним до поверхні векторомє тупим, це і визначає нижню частину поверхні. Для верхньої частини поверхнінаправляючі косинуси нормального вектора мають вигляд

, , . (2.2)

Нехай на обмеженій поверхні в кожній точці визначена деяка функція. Розглянемо інтегральну суму

(2.3)

де - площа проекції частиниповерхніна площину. При цьому величину вважатимемо додатною, якщо при проектуванні частинина площинунапрям обходу контура, що обмежує ю частину, не змінюється і від’ємною, якщо він змінюється на протилежний.

Означення. Скінченна границя інтегральних сум (2.3) при найдрібнішому поділі поверхні, яка не залежить від способу розбиття поверхні на частини, ні від вибору точок на них, називаєтьсяповерхневим інтегралом другого роду від функції по певній стороні поверхніі записується в наступному вигляді

(2.4)

Зауваження1. При заміні сторони поверхні на протилежну інтеграл змінює знак:

. (2.5)

Зауваження2. Оскільки між елементом площі проекції і елементом поверхнісправедливе співвідношення, то між поверхневими інтегралами другого і першого роду маємо зв'язок

, (2.6)

де - кут між нормаллю до поверхні в напрямку вибраної сторони і віссю.

Аналогічно можна проектувати поверхню на інші координатні площиниіі тоді отримаємо ще два поверхневі інтеграли:

, , (2.7)

, (2.8)

де ,- неперервні функції визначені на поверхні,- кути утворенні нормаллю до вибраної сторони поверхні і відповідно осямита.

Суму поверхневих інтегралів (2.6)-(2.8) називають загальним поверхневим інтегралом другого роду і записують у вигляді

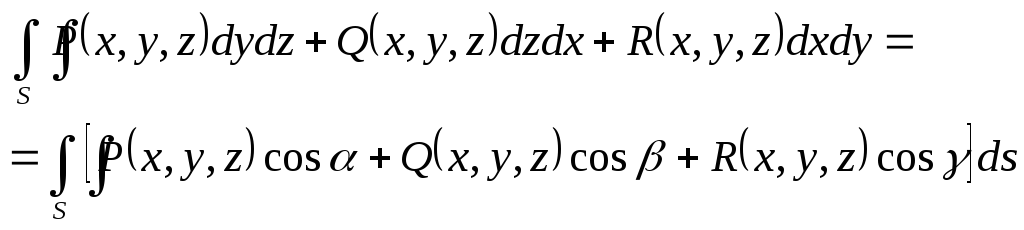(2.9)

Зауваження. У формулі (2.9) підінтегральний вираз представляє собою скалярний добуток вектора і одиничного вектора ,нормального до поверхні , направленого у вибрану сторону цієї поверхні. Тому формула (2.9) записується в коротшому вигляді:

. ((2.10)

Нехай гладка поверхня визначається рівнянням, тоді одиничний нормальний вектор до певної вибраної сторони поверхні має вигляд

Вибрана сторона поверхнітака, що кутміж нормаллю до поверхні і віссює гострим. Таким чином, враховуючи формулу (2.10), можемо записати зв'язок між поверхневими інтегралами першого і другого роду

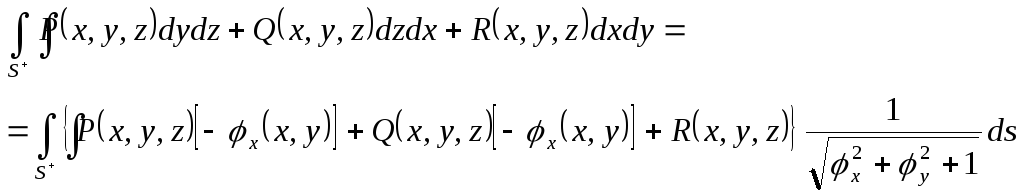. (2.11)

Якщо тепер згадати зведення поверхневого інтегралу першого роду до подвійного, при цьому елемент площі , то отримуємо формулу

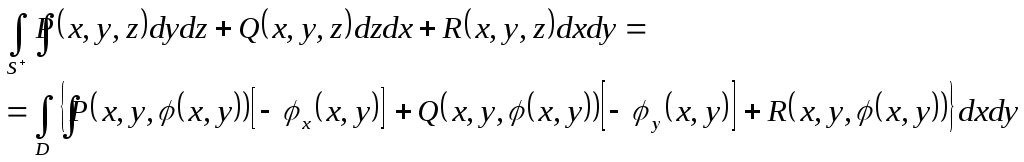(2.12)

Вибираючи протилежну сторону поверхні , а саме, одиничний вектор нормалі, до якої записується у вигляді:

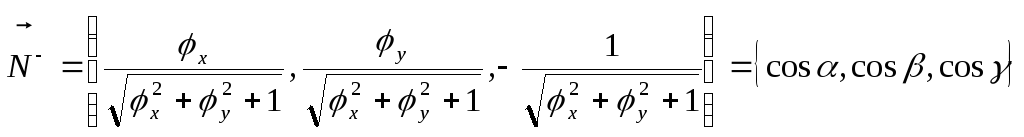(2.13)

Вибрана сторона поверхнітака, що кутміж нормаллю до поверхні і віссює тупим. Уже тепер поверхневий інтеграл другого роду зводиться до подвійного наступною формулою

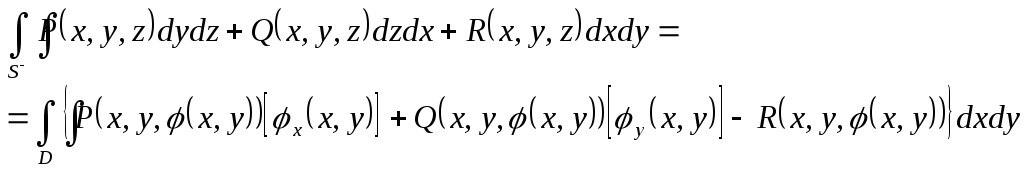(2.14)

Зауваження. Якщо до складу поверхні входить ділянкациліндричної поверхні, твірні якої паралельні осі, то

,

оскільки проекцією на площинубуде крива, площа якої є нульовою.

Якщо гладка двохстороння поверхня задана параметричними рівняннями

, , ,

то поверхневий інтеграл другого роду по одній з вибраних сторін цієї поверхні обчислюється за формулою

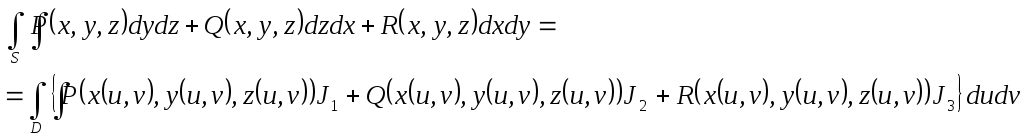де , , .

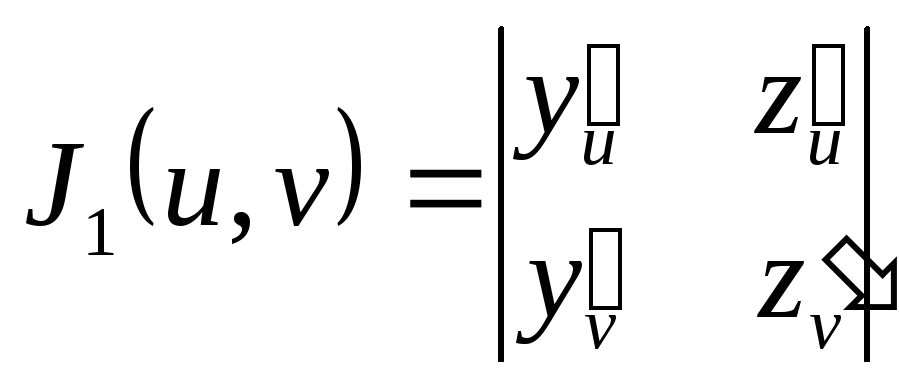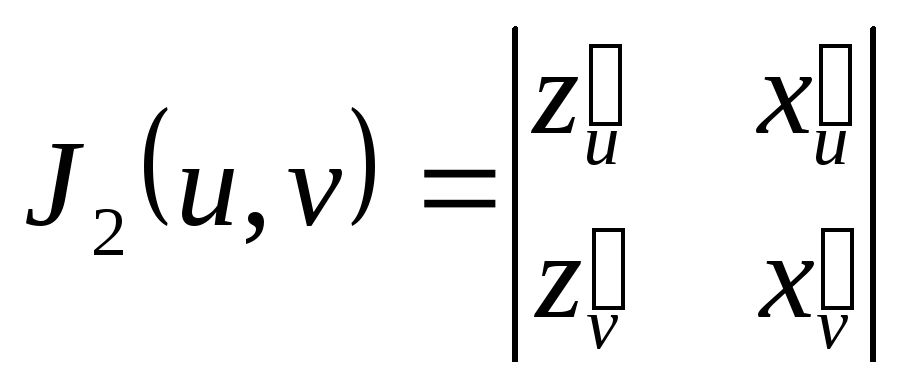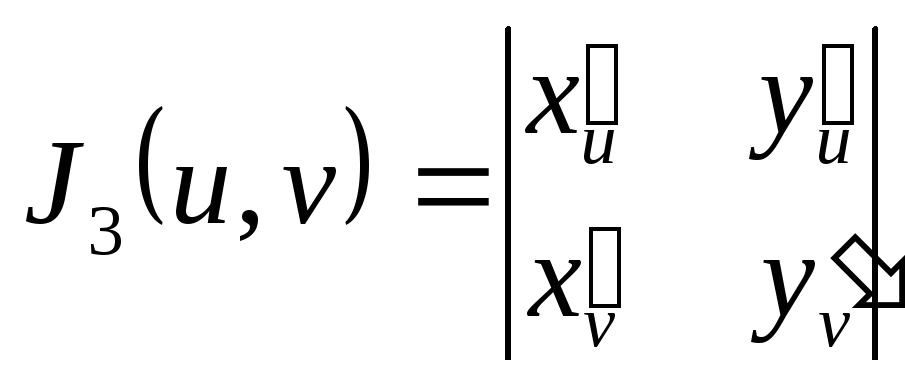Приклад 1. Обчислити поверхневий інтеграл другого роду

де - зовнішня сторона трикутника, утвореного перетином площини

з координатними площинами.

На основі формули (2.12), отримуємо

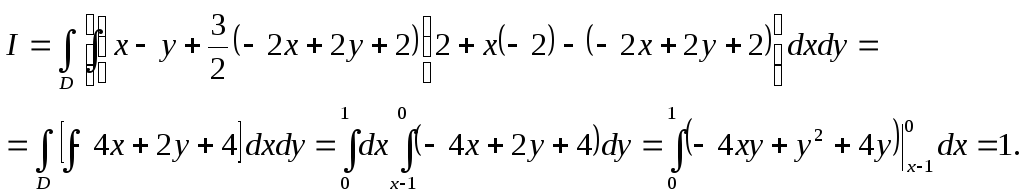
Приклад 2. Обчислити поверхневий інтеграл другого роду

де - частина поверхні , яка відтинається площиною , якщо нормаль до поверхні утворює з віссю тупий кут.

Графіком поверхні є параболоїд .

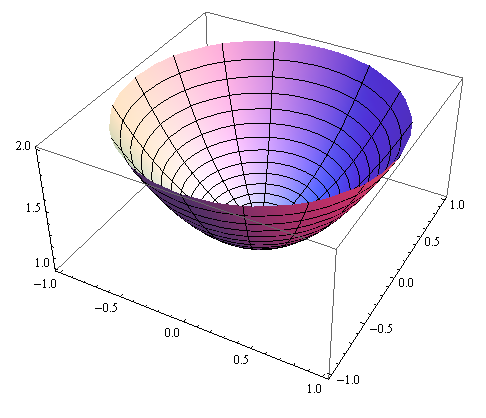
Ця поверхня визначається в явному вигляді,а тому скористаємось формулою (2.14), маємо і наш інтеграл зводиться до подвійного, який легко обчислюємо

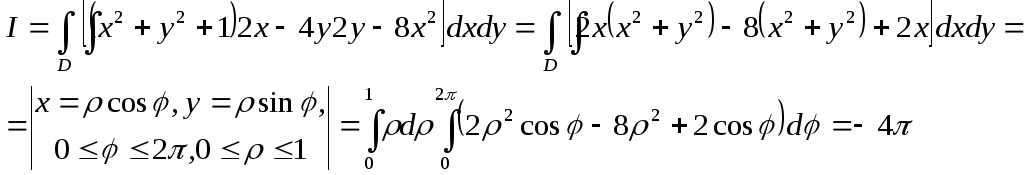
Приклади для самостійного завдання

Обчислити поверхневий інтеграл другого роду по вибраній стороні поверхні .

1. , де- частина поверхні параболоїда, яка відсікається площиною, сторона цієї поверхні вибрана так, що нормаль до неї утворює гострий кут з віссю.(Відповідь.)

2. , де- зовнішня сторона поверхні..(Відповідь 0.)

3. , де- зовнішня сторона поверхні куба, обмеженого площинами..(Відповідь 3.)

4. , де- зовнішня сторона поверхні.(Відповідь)

5. , де- верхня сторона площини, яка відсікається координатними площинами..(Відповідь 32)

6. , де- зовнішня сторона сфери, що лежить в першому октанті. .(Відповідь).

7. , де- зовнішня сторона сфери. .(Відповідь)

8. , де- верхня сторона площини, яка відсікається координатними площинами..(Відповідь)

9. , де- зовнішня сторона циліндра, що знаходиться між площинами.

10. , де- частина поверхні параболоїда,що вирізається циліндром. Сторона поверхні вибирається такою, що нормаль до неї утворює тупий кут з віссю.

11. , де- зовнішня сторона нижньої половини сфери..(Відповідь.)

12. , де- частина поверхні конуса, що лежить між площинами . Вибирається та сторона поверхні, нормаль до якої утворює тупий кут з віссю.(Відповідь.)

13. , де- частина поверхні параболоїда,що відтинається площиною . Сторона поверхні вибирається такою, що нормаль до неї утворює тупий кут з віссю .(Відповідь.)

14. , де- частина поверхні гіперболоїда, яка відтинається площинами . Вибирається та сторона поверхні, нормаль до якої утворює тупий кут з віссю.(Відповідь.)

15. , де- зовнішня сторона сфери, що лежить в першому октанті. (Відповідь.)

16. , де- частина поверхні параболоїда, що відтинається площиною . Сторона поверхні вибирається такою, що нормаль до неї утворює тупий кут з віссю .(Відповідь.)

17. , де- частина поверхні конуса, що відтинається площинами . Сторона поверхні вибирається такою, що нормаль до неї утворює гострий кут з віссю .(Відповідь:.)

18. , де- частина поверхні, що відтинається площиною . Сторона поверхні вибирається такою, що нормаль до неї утворює гострий кут з віссю .(Відповідь:.)

19. , де- частина поверхні конуса, що відтинається площинами . Сторона поверхні вибирається такою, що нормаль до неї утворює тупий кут з віссю .(Відповідь:.)

20. , де- частина поверхні параболоїда, що відтинається площиною . Сторона поверхні вибирається такою, що нормаль до неї утворює гострий кут з віссю .(Відповідь:.)

21. , де- внутрішня сторона циліндра, що відтинається площинами. (Відповідь:)

22. , де- зовнішня сторона замкненої поверхні, утвореної параболоїдомта півсферою. (Відповідь:.)

23. , де- зовнішня сторона сфери.. (Відповідь:.)

24. , де- зовнішня сторона циліндращо відтинається площинами. (Відповідь:.)

25. , де- частина поверхні параболоїда,

що відтинається площиною . Сторона поверхні вибирається такою, що нормаль до неї утворює гострий кут з віссю. (Відповідь:.)

26. , де- внутрішня сторона замкненої поверхні, утвореної конусомі площиною. (Відповідь:.)

27. , де- частина поверхні параболоїда, що відтинається площиною. Сторона поверхні вибирається такою, що нормаль до неї утворює гострий кут з віссю. (Відповідь:)

28. , де- частина поверхніконуса ,

що відтинається площинами . Сторона поверхні вибирається такою, що нормаль до неї утворює тупий кут з віссю. (Відповідь:.)

29. , де- частина поверхні параболоїда,що відтинається площиною. Сторона поверхні вибирається такою, що нормаль до неї утворює гострий кут з віссю. (Відповідь:0.)

30. , де- частина поверхніконуса ,що відтинається площиною. Сторона поверхні вибирається такою, що нормаль до неї утворює тупий кут з віссю. (Відповідь:.)

3.1 Формули Гауса-Остроградського та Стокса.

Формула Гауса-Остроградського встановлює зв'язок між поверхневим інтегралом другого роду по замкнутій поверхні і потрійним інтегралом по тілу, що обмежує ця поверхня. Записується ця формула в наступному вигляді

(3.1)

Доведемо цю формулу для області (тіла, обмеженого замкнутою поверхнею),простої, межа якої перетинається з будь-якою прямою, паралельною до координатних осей не більше ніж у двох точках. Нехай замкнена область, зверху і знизу обмежена гладкими поверхнями:

- зверху (),- знизу (). Нехай проекцією областіна площинує область, тоді можна записати

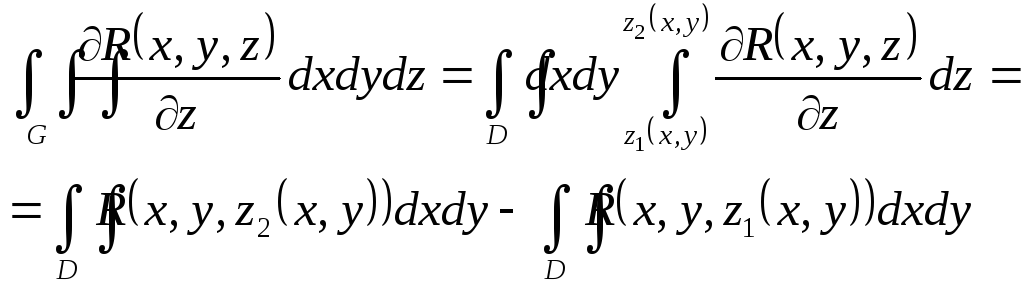(3.2)

Отримані два інтеграли це вже обчислені поверхневі інтеграли:

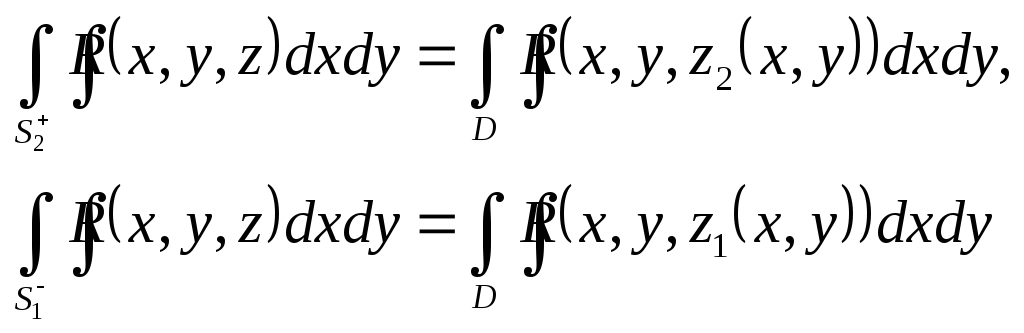
Віднімаючи отримані дві рівності, отримуємо

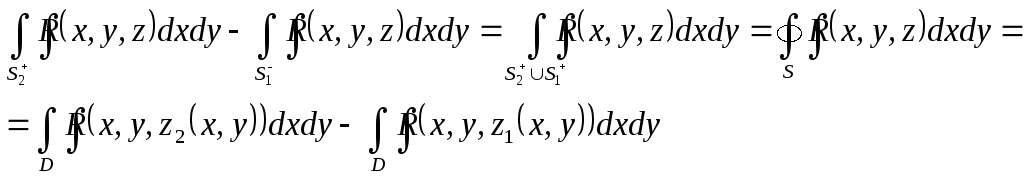
Таким чином, із рівності (3.2) видно

(3.3)

Аналогічно отримуємо рівності

(3.4)

(3.5)

Додавши почленно рівності (3.3)-(3.5), отримуємо формулу Гауса-Остроградського (3.1).

Зауваження. Формула (3.1) справедлива і для довільної замкненої області , яку можна розбити на скінчене число простих областей,.

Приклад 1. Обчислити інтеграл

де - зовнішня сторона замкнутої поверхні, яка розміщена в першому октанті і складається з циліндраі площин.

В нашому випадку маємо . Користуючись формулою Гауса-Остроградського (3.1), отримуємо

Приклад 2. Обчислити поверхневий інтеграл другого роду

де - нижня сторона параболоїда, що відсікається площиною .

Дана поверхня не є замкнена. Доповнимо її до замкненої частиною площини . Позначимо плоску частину і виберемо її верхню сторону. Для обчислення інтегралу по замкнутій поверхні застосуємо формулу Гауса-Остроградського, отримуємо

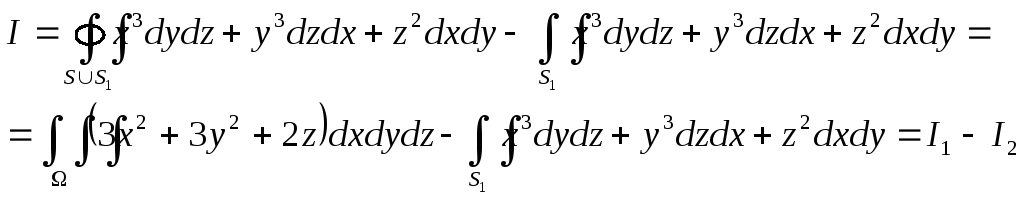
Проекцією тіла на площину є круг обмежений колом . Інтеграл зведемо до подвійного по цій проекції і перейдемо до полярної системи координат , враховуючи , :

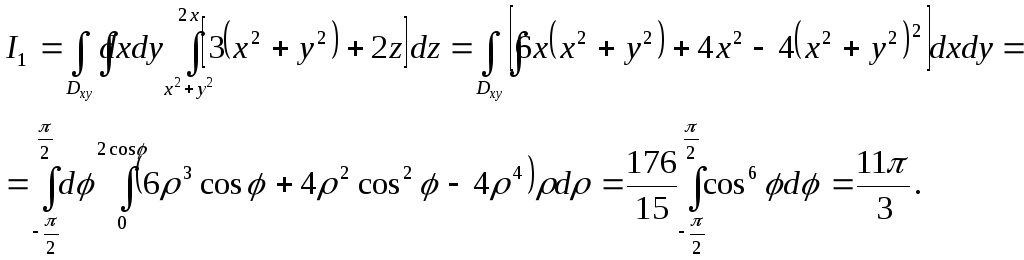
Тепер обчислюємо інтеграл , який розглядається по поверхні . Обчислюючи зовнішню нормаль до площини , маємо .

Таким чином, отримуємо

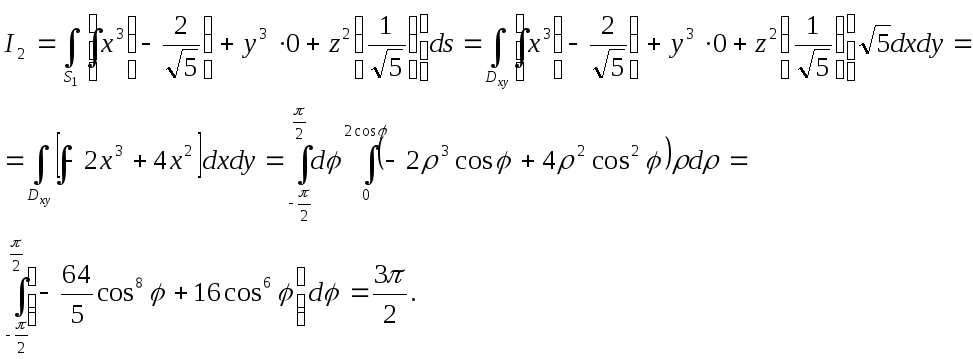
Відповідь: .

Приклад 3. Обчислити поверхневий інтеграл другого роду

де - замкнена поверхня, яка утворюється при перетині параболоїда , площиною . Вибирається зовнішня сторона цієї поверхні.

Застосовуючи формулу Гауса-Остроградського (3.1), в нашому випадку отримуємо.

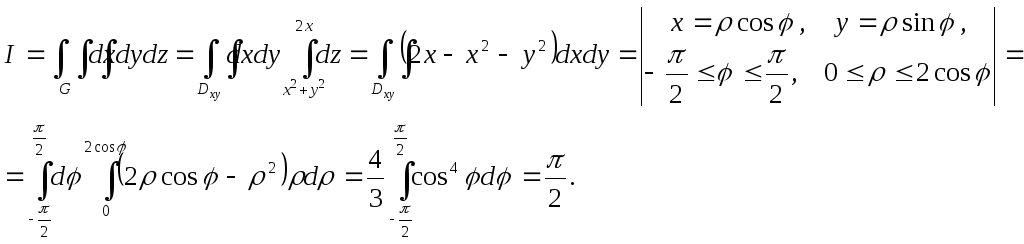
Формула Стокса встановлює зв’язок між поверхневим та криволінійним інтегралом по просторовій криві, яка є межею поверхні.

Нехай - деяка гладка, обмежена частина поверхні, задана рівнянням , змінюються в деякій обмеженій області . Можна говорити, що це є проекція поверхні на площину . Позначимо через контур, який обмежує поверхню , а - проекція контура на площину , тобто

- межа області . Припустимо, що на поверхні визначена функція , яка є неперервною разом з частинними похідними першого порядку.

Обчислимо криволінійний інтеграл другого роду по замкнутому контуру : . Оскільки контур лежить на поверхні , то координати його точок задовольняють рівняння , причому .

Застосовуючи формулу Гріна, отримуємо

Оскільки вибрана верхня сторона поверхні (), то нормаль до поверхні . Таким чином і отримуємо

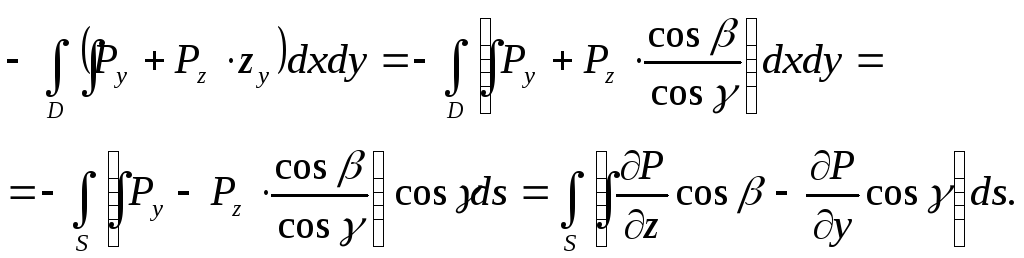
Отже, маємо рівність

(3.6)

Аналогічно отримуємо рівності

(3.7)

(3.8)

Додаючи три рівності (3.6)-(3.8), отримуємо формулу Стокса:

(3.9)

Зауваження 1.Для того, щоб простіше запам’ятати формулу Стокса, запишемо її в наступному вигляді:

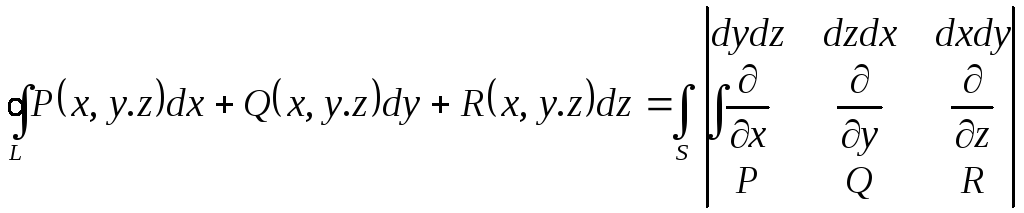(3.10)

При цьому визначник справа формально розкриваємо по верхньому рядку.

Зауваження 2. З формули Стокса випливають умови, при яких вираз

є повним диференціалом деякої функції

, тобто . Ці умови записуються у вигляді трьох тотожностей:

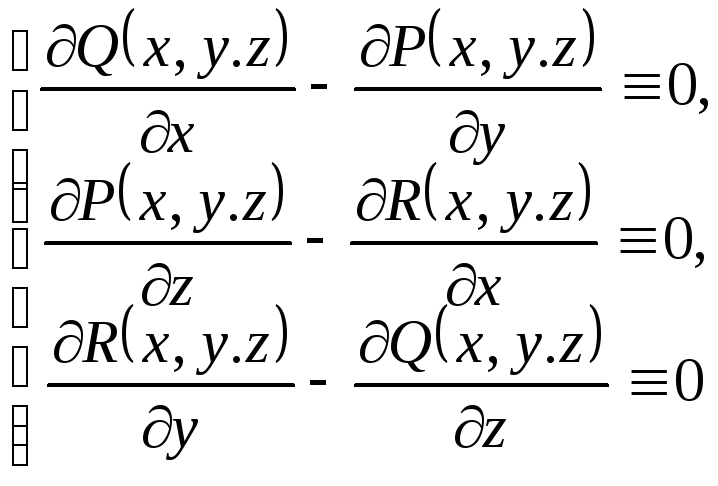(3.11)

Тотожності (3.11) записуються в більш короткій формі:

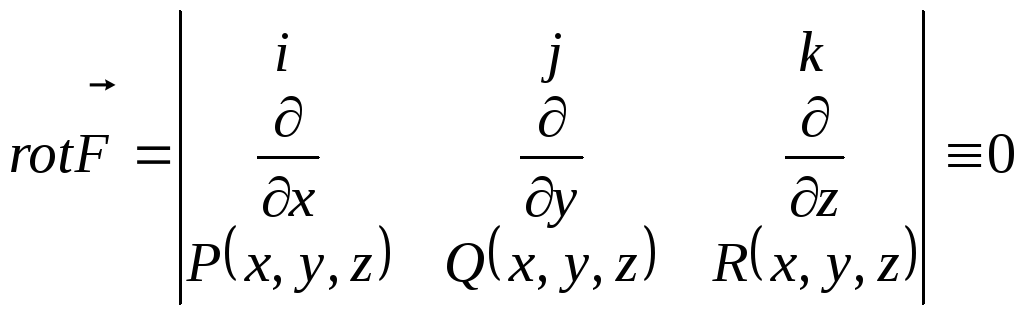(3.12)

При виконанні тотожностей (3.11) криволінійний інтеграл

не залежить від шляху інтегрування, а залежить тільки від початкової точки і кінцевої і обчислюється безпосередньо:

.

Приклад1. Обчислити криволінійний інтеграл

по замкнутому контуру , який утворюється при перетині сфери і конуса ,. Контур обходиться в додатному напрямку. Обчислити двома способами: а)безпосередньо; б)за формулою Стокса.

а) Контур інтегрування є коло: , яке лежить у площині. Запишемо параметричне рівняння цього кола, маємо. Звідси безпосередньо отримуємо

.

б)За поверхню інтегрування вибираємо круг, який лежить у площині. Очевидно, направляючі косинуса вектора нормалі,

, , а звідси із формули (3.10) отримуємо

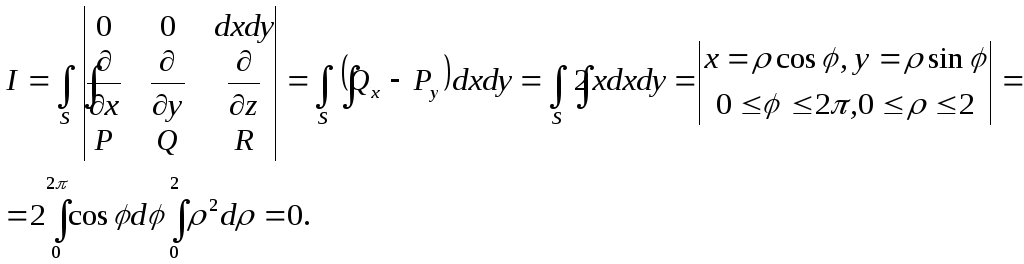
4.1 Застосування поверхневих інтегралів в задачах механіки та геометрії

Нагадаємо кілька означень, які стосуються системи матеріальних точок.

1.Маса матеріальної поверхні з густиною маси розподіленої на цій поверхні за формулою обчислюється з допомогою поверхневого інтегралу першого роду:

(4.1)

2.Координати центра мас матеріальної поверхні з густиною маси розподіленої на ній обчислюються за формулами:

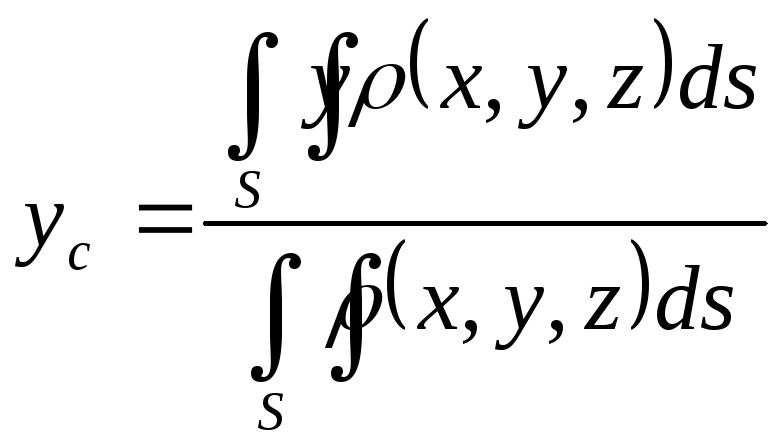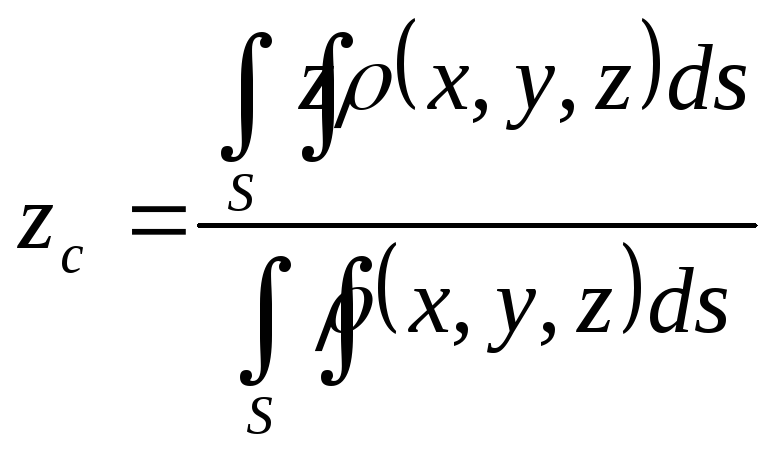, ,. (4.2)

Зауважимо, що у формулах (4.2) у знаменнику є маса матеріальної поверхні (формула (4.1)), а в чисельниках – відповідністатичні моменти:

-статичний момент відносно площини , позначається ,

-статичний момент відносно площини ,

-статичний момент відносно площини .

3.Моменти інерції матеріальної поверхні відносно координатних осей,,та початку координатзнаходять за формулами:

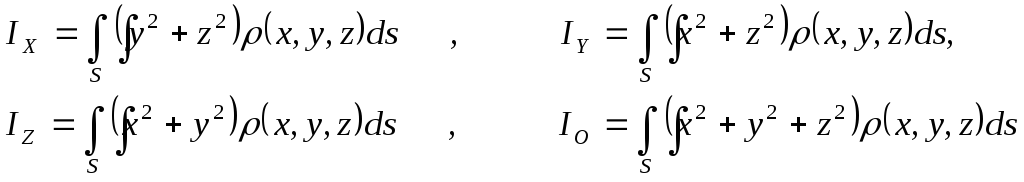. (4.3)

Розглянемо приклади.

Приклад 1. Знайти координати центра мас однорідної поверхні конуса

Оскільки вісь є віссю симетрії цього конуса, то центр мас знаходиться на осі, отже . Координату знаходимо за першою з формул (4.2), поклавши :

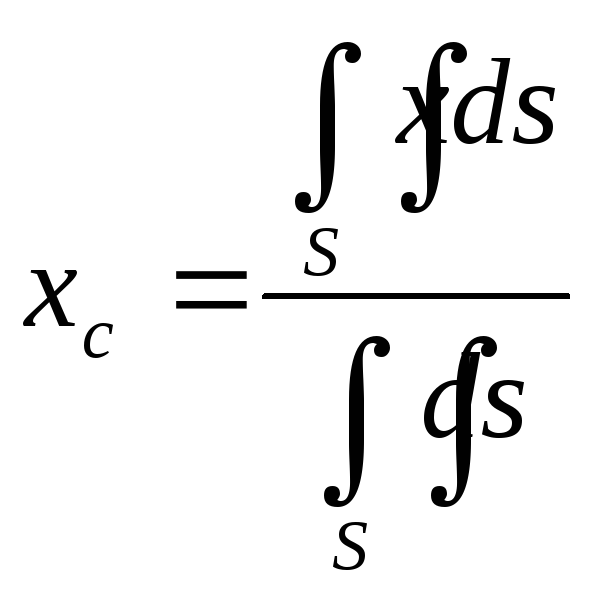
Інтеграл в знаменнику дорівнює площі бічної поверхні конуса, яка дорівнює , для нашого випадку, а це означає рівність.

Обчислюючи інтеграл в чисельнику, отримуємо

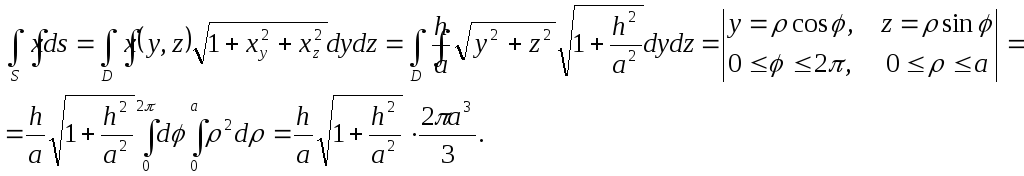
Звідси отримуємо

.

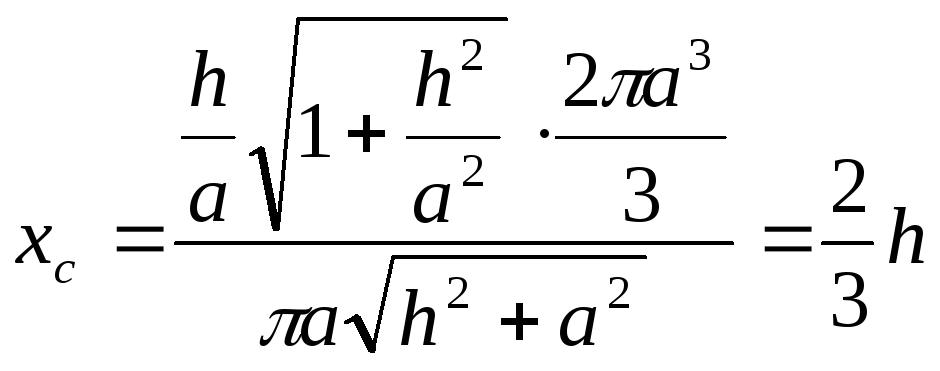Приклад 2. Знайти момент інерції відносно осі однорідної сферичної оболонки,.

Момент інерції відносно вказаної осі обчислюємо за формулою

.

Поверхня записується у явному вигляді: . Звідси отримуємо

,

.

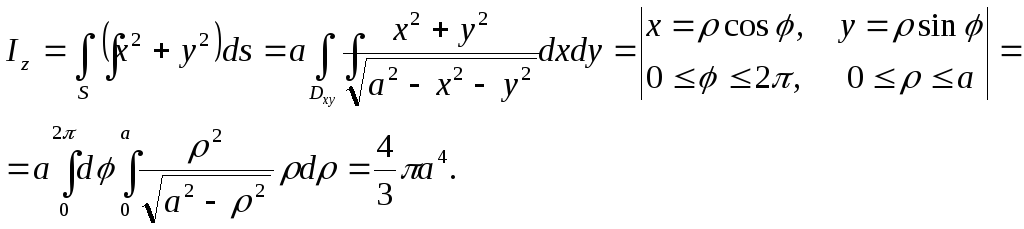Задачі для самостійної роботи.

Обчислити поверхневі інтеграли першого роду.

1. , де-частина площини, що лежить в 1-му октанті.

2. , де-поверхня тіла, заданого нерівностями.

3. , де-частина конічної поверхні, вирізана циліндром

Обчислити поверхневі інтеграли другого роду.

4. , де-нижня сторона частини конусапри.

5. , де-зовнішня сторона трикутника, утвореного при перетині площиниз координатними площинами.

6. , де-зовнішня сторона сфери.

7. , де-зовнішня сторона циліндра, з основами

та .

За формулою Гауса-Остроградського обчислити поверхневі інтеграли по зовнішній стороні поверхні.

8., де-поверхня тіла обмеженого площинами

.

9. , де-сфера.

10. , де-частина поверхніпри. (вказівка: доповнити поверхню до замкненої).

Використовуючи формулу Стокса, обчислити криволінійні інтеграли.

11., де-замкнений контур, утворений при перетині параболоїдаз координатними площинами.

12., де-виток гвинтової лінії,,,, що обходиться у напрямку від точкидо точки. (вказівка: доповнити криву відрізком до замкненого контура).

13.Знайти масу півсфери , якщо поверхнева густина в кожній її точці дорівнює.

14.Знайти координати центра маси конічної поверхні , якщо її поверхнева густина маси в кожній точці є пропорційна відстані від цієї точки до осі конуса.

15. Знайти статичні моменти відносно координатних площин однорідної трикутної пластини ,.

16.Знайти момент інерції відносно осі частини однорідної конічної поверхні,, що знаходиться всередині циліндра,.

Відповіді. 1.. 2.. 3.. 4.. 5.. 6.. 7.. 8..

9.. 10.. 11.. 12.. 13.. 14.. 15.. 16..