
Лекция №1
Основы механики
Элементы кинематики
Основные понятия кинематики материальной точки
1. Материальная точка. Материальной точкой (или точечным телом) называют тело, размерами которого можно пренебречь в данной задаче. (Привести примеры).
2. Система отсчёта. Механическим движением называется изменение взаимного расположения тел или частей одного и того же тела в пространстве с течением времени. О механическом движении можно говорить, если указана система отсчёта. Система отсчёта включает в себя:
1) Тело отсчёта, т.е. тело, которое условно принимается за неподвижное и относительно которого рассматривается движение других тел. С телом отсчёта связывают систему координат. 2) Прибор для измерения времени.
3.
Радиус-вектор.
Положение материальной точки в
пространстве определяется радиус-вектором
![]() ,
т.е. вектором, проведённым из начала
координат в данную точку.
,
т.е. вектором, проведённым из начала
координат в данную точку.
4. Траектория движения. Воображаемая линия, которую описывает материальная точка при движении, называется траекторией. Форма траектории зависит от выбора системы отсчёта, т.е. форма траектории — понятие относительное. (Привести примеры).
5. Перемещение.
Путь.При описании движения тела надо
уметь определять изменение его положения.
С этой целью вводятся понятия перемещения
тела и пути, пройденного им.Перемещением
называется вектор, проведённый из
начального положения материальной
точки в конечное положение (вектор![]() на рис. 1). Длину участкаl,
пройденного материальной точкой по
траектории, называютпутёмилидлиной пути.
на рис. 1). Длину участкаl,
пройденного материальной точкой по
траектории, называютпутёмилидлиной пути.
Рис. 1![]() .
Тогда скоростью
.
Тогда скоростью![]() называют отношение
называют отношение
![]() (1)
(1)
т.е.
скорость —
это перемещение, совершённое за единицу
времени при условии, что она остаётся
неизменной.
С
точки зрения математики скорость
является производной радиус-вектора
по времени, поскольку элементарное
перемещение и элементарный промежуток
времени можно рассматривать как
дифференциалы радиус-вектора
![]() (функции) и аргументаt.
В любой точке траектории скорость,
которая является вектором, направлена
по касательной к ней. В системе единиц
СИ единицей скорости является 1 м/с.
(функции) и аргументаt.
В любой точке траектории скорость,
которая является вектором, направлена
по касательной к ней. В системе единиц
СИ единицей скорости является 1 м/с.
7. Ускорение.Быстроту изменения скорости характеризуют
ускорением. Пусть в течение элементарного
промежутка времениdtэлементарное
изменение скорости равно![]() .
Тогда ускорение
.
Тогда ускорение![]() находится по формуле
находится по формуле
![]() (2)
(2)
Таким образом, ускорениеэто изменение скорости за единицу времени. С точки зрения математики ускорениепроизводная скорости по времени. В системе единиц СИ единица ускорения — 1 м/с2.
Скорость тела в
общем случае изменяется как по модулю,
так и по направлению. Поэтому при
криволинейном движении вектор ускорения
составляет некоторый угол с вектором
скорости. Разложим вектор ускорения на
две составляющие: вдоль направления
скорости и перпендикулярно к ней
(рис. 2). Составляющая
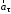 направлена по касательной к траектории
движения либо по направлению скорости,
либо против неё. Поэтому её называют
касательным или тангенциальным
ускорением. Оно характеризует быстроту
изменения скорости только по модулю и
вычисляется по формуле:
направлена по касательной к траектории
движения либо по направлению скорости,
либо против неё. Поэтому её называют
касательным или тангенциальным
ускорением. Оно характеризует быстроту
изменения скорости только по модулю и
вычисляется по формуле:
 (3)
(3)
Составляющая
![]() направлена перпендикулярно к скорости.
Поэтому она называется нормальным
ускорением. Оно характеризует быстроту
изменения скорости только по направлению
и вычисляется по формуле:
направлена перпендикулярно к скорости.
Поэтому она называется нормальным
ускорением. Оно характеризует быстроту
изменения скорости только по направлению
и вычисляется по формуле:
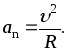 (4)
(4)
Рис. 2
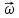 =
=
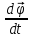 . (5)
. (5)
Рис. 3
Для характеристики
быстроты изменения угловой скорости
вводят понятие углового ускорения.
Пусть за элементарный промежуток времени
dt угловая скорость изменилась на
величину![]() Тогда угловое ускорение
Тогда угловое ускорение![]() равно
равно
![]() (6)
(6)
т.е. угловое ускорение — изменение угловой скорости за единицу времени. С точки зрения математического анализа угловое ускорение — производная угловой скорости по времени.
В системе единиц СИ единицей угловой скорости является 1 рад/с, а углового ускорения —1 рад/с2.
