lecture_kaumov

Отсюда:

Перечислим использованные обозначения.

vB - искомый прогиб в точке B (от рабочих нагрузок);

T =1 – единичная сила, приложенная в интересующем нас направлении искомого прогиба vB в интересующей нас точке В.

Mx(T) - изгибающий момент в фиктивной задаче о приложении к балке силы Т в точке В.

Mx(q) - изгибающий момент от рабочих нагрузок.

Еще раз напомним, что физический смысл формулы Мора заключается в том, что работа силы Т на искомом перемещении vВ равна работе внутренних сил, вызванных этой силой, на деформациях от внешних сил.

Примечания.

1.Для удобства вычислении обычно принимают, что Т=1.

2.Работой касательных напряжений обычно пренебрегают ввиду ее малости по сравнению с W.

3. При необходимости вычисления угла наклона балки α вместо единичной фиктивной силы Т необходимо прикладывать единичный момент m=1 в интересующей нас точке. Формула Мора примет вид

l

m B 1 Mx(m)Mx(q)ds. EJx 0

16.1.1 Методы вычисления интегралов. Формулы трапеций и Симпсона

Для приближенного вычисления интегралов существует много разных методов. Пусть надо найти:

m

I y(x) dx ?

n

101

Для вычисления интеграла Мора часто используют метод Верещагина. Однако более удобными являются приближенные методы.

Рис. 16.5

Формула трапеций

Разобьем интервал n,m на малые интервалы (например, на рис.16.5.

их четыре). Поскольку по геометрическому смыслу интеграл представляет собой площадь фигуры mnkl, то С можно вычислить приближенно, представив ее в виде суммы площадей четырех трапеций:

Формула Симпсона

Формула Симпсона намного точнее формулы трапеций (хотя может показаться менее удобной). Она имеет вид:

При этом в отличие от метода трапеций, отрезок а должен разбиваться на равные интервалы x1 x2 . Аналогично, должно быть x3 x4

Примечание. Для прикидочных грубых оценок можно использовать формулу:

a в

I 6 y1 4 y3 y5 .

16.2. Вычисление прогибов на основе решения дифференциального уравнения изогнутой оси балки

Прогибы можно находить и другими способами, например, на основе решения дифференциального уравнения изогнутой оси балки. Для вывода этого уравнения, рассмотрим элемент балки (рис.16.6).

102

Рис.16.8

Вычисляем , учитывая, что yD h . Согласно определению

2

DH ds.

16.2.1. Решение дифференциального уравнения изогнутой оси балки

Если балка имеет постоянную толщину, то есть Jx const , то решение легко записывается в общем виде:

104

участках балки Mx разные, а значит C и D также разные (в частности, если балка имеет три участка, то нужно определить 6 констант).

Однако существует способ интегрирования, который сводит все неизвестные только к двум константам (разработан Клебшом)

16.2.2. Правила Клебша

Правила Клебша сводятся к следующему.

1) Mx выражаем через внешние силы, которые лежат только слева (или только справа) от сечения.

2) Если погонная сила q не доходит до правого конца, то ее доводим до этого правого конца и уравновешиваем ее снизу (рис.16.9).

При выполнении этих условий все константы С на разных участках будут одинаковы. Аналогично будут одинаковы все константы D.

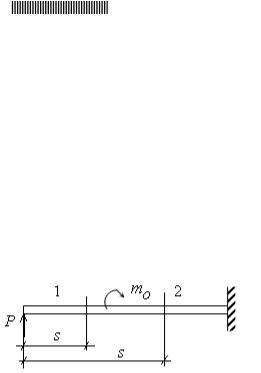
Справедливость этого утверждения доказывается непосредственной проверкой, то есть подстановкой решения в условия стыковки решения на границе участков. Рассмотрим, например, случай, приведенный на рис.16.10.

рис16.10

По правилам Клебша момент Mx на участках (I), (II) запишем в виде:

(I): Mx P s

(II): Mx P s m0(s a)0

Дифференциальные уравнения на участках:

105

Отсюда видно, что при s = a получим равенство углов наклона и прогибов, вычисленных по разным формулам при любых С и D, т.е. условия гладкости изогнутой оси выполняются. Аналогично проверяются условия гладкости на границе участка, на которой заканчивается погонная сила q.

16.2.3Условия для определения С и D

1)Первый случай . Рассмотрим балку, лежащую на двух опорах

(см. рис.16.11).

Опять получили два уравнения для С и D.

106

Пример вычисления прогиба

Пусть необходимо вычислить прогиб в центре балки длины l, загруженной погонной силой q. Решим эту задачу двумя способами.

Ввиду симметричности схемы можно сразу найти реактивные силы – они будут равны ql/2. Тогда изгибающий момент в сечении на расстоянии s

Первый способ. Использование дифференциального уравнения изогнутой оси балки.

Находим прогиб в центре балки (при s = l/2):

Второй способ. Использование интеграла Мора

Метод дал ошибку в 5%.

3. Метод Симпсона по 2-м участкам.

107

Таким образом, метод Симпсона в этом примере дает точное решение.

16.2.4. Балки на упругом основании. Закон Винклера

Рассмотрим основание (грунт) Приложим к мерному стержню силу Р (рис.16.14), тогда осадка стержня v, будет тем больше, чем больше сила Р.

Рис.16.14

Запишем это утверждение аналитически:

P k v.

Здесь k - называется коэффициентом постели. Эта зависимость называется

законом Винклера.

Согласно III-му закону Ньютона реакция грунта R=P. Приведем закон

к виду, когда задаётся погонная сила q (cм. рис.16.15).

q

Р

a

R

r

Рис.16.15

Ее равнодействующая должна быть равна Р, т.е. q a P;

Отсюда

108

Обозначая k k получим

16.4. Уравнение изогнутой оси балки на упругом основании

Рассмотрим балку, которая лежит на грунте.

q

r

Рис.16.16

Такой моделью описывается поведение ленточных фундаментов, дорожных полотен, обшивок трехслойных панелей типа сэндвич.

Грунт противодействует внешним силам некоторой погонной силой r . Выразим ее через прогиб (s). Для этого вырежем малый элемент (см. рис.16.16). Сравнивая рис.16.14 и рис.16.16 видим, что элемент балки, фактически представляет собой мерный стержень, для которого реакция определяется по формуле (16.16), т.е. реакция балки с прогибом связана соотношением:

r k v.

Далее запишем уравнения равновесия элемента балки и уравнение ее изогнутой оси

s

109

Здесь знак «-» перед k' v поставлен потому, что осадка v элемента имеет отрицательный знак, а реакция должна быть противоположна погонной силе qвнешн .

Подставим (16.18) в (16.20):

Решение запишем в виде суммы:

v vодн vчаст .

Простой подстановкой в (16.21) можно проверить, что решение имеет вид:

(условий закрепления) и условий статики на концах балки.

16.5. Бесконечная балка на упругом основании

Этой моделью можно описать, например, поведение дорожного полотна с автомобилем веса Р. Погонная сила qвнеш qвеса представляет собой погонный вес полотна. Мы можем общее решение представить как сумму

qвнеш 0, P 0. Рассмотрим этот случай. Пусть s – расстояние от силы Р до сечения. Слева и справа прогиб симметричный, поэтому исследуем прогиб v только справа, то есть, найдем функцию v(s).

Рис.16.17

110