13. Расчет изменения энтропии реакции при стандартной и нестандартной температурах (на примере реакций с участием неорганических веществ)

Термодинамическая энтропия S, часто просто именуемая энтропия, в химии и термодинамике является функцией состояния термодинамической системы.

1) теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому

2) невозможен процесс, единственным результатом которого является превращение теплоты в работу

Энтропия как критерий направления процессов. В изолированной системе протекают только процессы, в которых энтропия увеличивается. Энтропия есть мера упорядоченности системы.

Цикл Карно: состоит из четырех участков и изображается PV-диаграммами. Процессы 1-2, 3-4 явл-ся изотерм., процессы 2-3, 4-1 явл-ся адиабатическими.

1-2: Пусть газ нах-ся в точке 1 с темп Т₁, давл Р₁ и объемом V₁. Про изотерм. Расширении газ преходит в состояние 2 с давл Р₂, V₂, но Т₁. Темп не меняется, значит не меняется внутр. Энергия. Чтобы газ изотерм. Расширялся, он должен получить от нагр Q₁. При изотрем. Расширении Q₁=W₁

2-3: из сост 2 газ адиабатически расширяется до сост 3. Р₃, V₃, Т₂<T₁. Падение Т связано с работой газа при адиабатическом расширении, тепло не подводится и газ совершает работу за счет своей внутр энергии, в результате газ охлаждается W₂=-ΔU

3-4: из сост 3газ изотерм сжимается до сост 4, характеризуемого параметрами V₄, P₄, T₂. Над газом совершается работа при данном изотерм проц ΔU=0

4-1: из сост 4 газ адиабатно сжимается так, что он принимает исх парметры P₁, V₁, T₁. Над газом совершается работа, газ нагревается до T₁, т.к. теплоотдачи при адиабатическом проц нет –ΔW=ΔU

Уравнения для расчета энтропии для различных систем:

1. Изотермический процесс (Т=const): ΔS= (V=const) ΔS=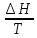 (P=const)

2. Изобарный процесс (P=const): ΔS=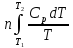; ΔC_p=const; ΔS=nC_pln

3. Изохорный процесс (V=const): ΔS=; ΔC_v=const; ΔS=nC_vln

Для различных процессов с идеальным газом

При ΔC_v=const

ΔS=nC_vln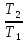 + nRln

Если C_p=C_v-R

ΔS=nC_pln + nRln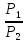

В изотермическом процессе

ΔS=nC_pln= nRln

В изобарном процессе

ΔS=nC_pln= nRln

В изохорном процессе

ΔS=nC_pln= nRln

Расчет изменения энтропии хим. Р-ции

А₁ + А₂ = А₃ + А₄

Т=298

+ --

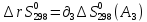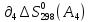T≠298

1. ΔC_p=const

2. ΔC_p не зависит от Т

для неорг. Вв

для орг. В-в

14.Изохорно-изотермический потенциал, его свойства, применение в качестве критерия направленности процесса.

Термодинамическими потенциалами, или характеристическими функциями, называют термодинамические функции, посредством которых и их производных по соответствующим независимым переменным (естественным) могут быть выражены в явном виде все термодинамические свойства си-мы. Это означает, что характеристические функции содержат в себе всю термодинамическую информацию о си-ме. Наибольшее значение имеют четыре основных термодинамических потенциала (П_ав):

1) внутренняя энергия U(S,V),

2)Энтальпия H(S,p)=U+pV,

3)энергия ГельмгольцаF(T,V)=U-TS,

4)энергия ГиббсаG(T,p)=H-TS=F+pV.

В скобках указаны естественные переменные для термодинамических потенциалов. Все эти потенциалы имеют размерность энергии и все они не имеют абсолютного значения, поскольку определены с точностью до постоянной, которая равна внутренней энергии при абсолютном нуле.

ϬQ=dU+ϬA, ϬA=pdV+ϬA', ϬQ=dU+pdV+δA' – первый закон термодинамики.

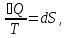ϬQ=TdS – второй закон термодинамики.

Зависимость термодинамических потенциалов от их естественных переменных описывается основным уравнением термодинамики, которое объединяет первое и второе начала: TdS=dU+ PdV=ϬA' => A'_max= TdS-dU- PdV.

Рассмотрим А_max при V=const, T=const

A’_max= TdS – dU = -d(U - TS)

U - TS=F – свободная энергия Гельмгольца

A’_max= -dF – изохорно-изотермический потенциал

В зависимости от условия протекания процесса различают ; термодинамических потенциала

П_A,B

A'_max=-П_АВ- т.е во всех случаях A'_max= убыли соответствующих термодинамических потенциалов.

A'_max=-П_АВ- для обратимых процессов, A'_max<-П_АВ- для необратимых процессов, A'_max>=-П_АВ- для любых процессов.

A'_max=0, т.е си-ма находится под влиянием давления.

∆П_АВ<0 при любом самопроизвольном процессе термодинамический потенциал уменьшается и его можно использовать, как критерий направления процесса:

1. Если процесс идет самопроизвольно прямо, тогда П_АВ уменьшается и процесс идет в прямом направлении.

2. Если П_АВ уменьшается и в момент равновесия имеет минимальные значения или П_АВ равно 0, тогда процесс идет в обоих направлениях.

3. Если П_АВ больше 0, то процесс идет в обратную сторону, т.е не самопроизвольно.