42. Энергия активации, ее физический смысл. Методы определения энергии активации.

Энергия активации - минимальное количество энергии, которое требуется сообщить системе (джоуль на моль), чтобы произошла реакция. Термин введён Сванте Августом Аррениусом в 1889. Типичное обозначение энергии реакции E_a

В химической модели, известной как Теория активных соударений, есть три условия, необходимых для того, чтобы произошла реакция:

• Молекулы должны столкнуться. Это важное условие, однако его не достаточно, так как при столкновении не обязательно произойдёт реакция.

• Молекулы должны обладать необходимой энергией (энергией активации). В процессе химической реакции взаимодействующие молекулы должны пройти через промежуточное состояние, которое может обладать большей энергией. То есть молекулы должны преодолеть энергетический барьер; если этого не произойдёт, реакция не начнётся.

• Молекулы должны быть правильно ориентированы относительно друг друга.

При низкой (для определённой реакции) температуре большинство молекул обладают энергией меньшей, чем энергия активации, и неспособны преодолеть энергетический барьер. Однако в веществе всегда найдутся отдельные молекулы, энергия которых значительно выше средней. Даже при низких температурах большинство реакций продолжают идти. Увеличение температуры позволяет увеличить долю молекул, обладающих достаточной энергией, чтобы преодолеть энергетический барьер. Таким образом повышается скорость реакции.

Уравнение Аррениуса устанавливает связь между энергией активации и скоростью протекания реакции:

k — константа скорости реакции, A — фактор частоты для реакции, R — универсальная газовая постоянная, T — температура в кельвинах.

С повышением температуры растёт вероятность преодоления энергетического барьера.

Для количественного описания температурных эффектов в химической кинетике для приближённых вычислений кроме уравнения Аррениуса используют правило Вант-Гоффа: повышение температуры на 10 К увеличивает для большинства реакций скорость в 2-4 раза. Математически это означает, что скорость реакции зависит от температуры степенным образом:

где γ — температурный коэффициент скорости (его значение лежит в интервале от 2 до 4). Правило Вант-Гоффа является весьма грубым и применимо только в очень ограниченном интервале температур.

Переходное состояние — состояние системы, при котором уравновешены разрушение и создание связи. В переходном состоянии система находится в течение небольшого (10⁻¹⁵ с) времени. Энергия, которую необходимо затратить, чтобы привести систему в переходное состояние, называется энергией активации. В многоступенчатых реакциях, которые включают в себя несколько переходных состояний, энергия активации соответствует наибольшему значению энергии. После преодоления переходного состояния молекулы вновь разлетаются с разрушением старых связей и образованием новых или с преобразованием исходных связей. Оба варианта возможны, так как происходят с высвобождением энергии. Существуют вещества, способные уменьшить энергию активации для данной реакции. Такие вещества называют катализаторами. Биологи же такие вещества называют ферментами.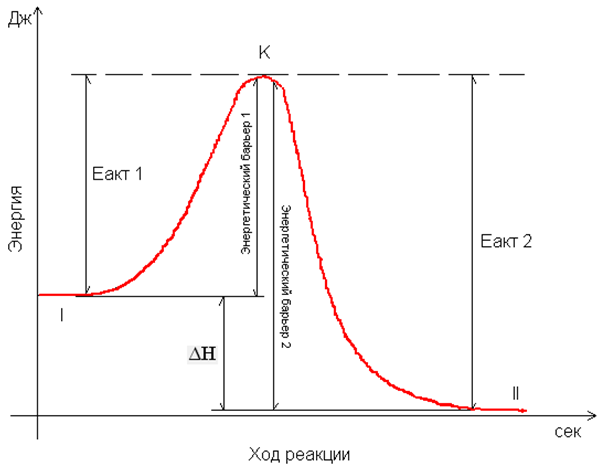 I - энергетический уровень до реакции

II - более низкий энергетический уровень после реакции

ΔН - выделившиеся энергия в ходе реакции

К – уровень наименьшего запаса энергии, для взаимодействия молекул

Е_{акт 1} - энергия активации прямой реакции

Е_{акт 2} - энергия активации обратной реакции

В большинстве случаев для расчета энергии активации Е_а по экспериментальным данным используют интегральную форму уравнения Вант-Гоффа-Аррениуса или его запись в виде:

lgK = lgKo - Е а/2,303 RT (9)

Следовательно, lgK линейно зависит от обратной абсо­лютной температуры

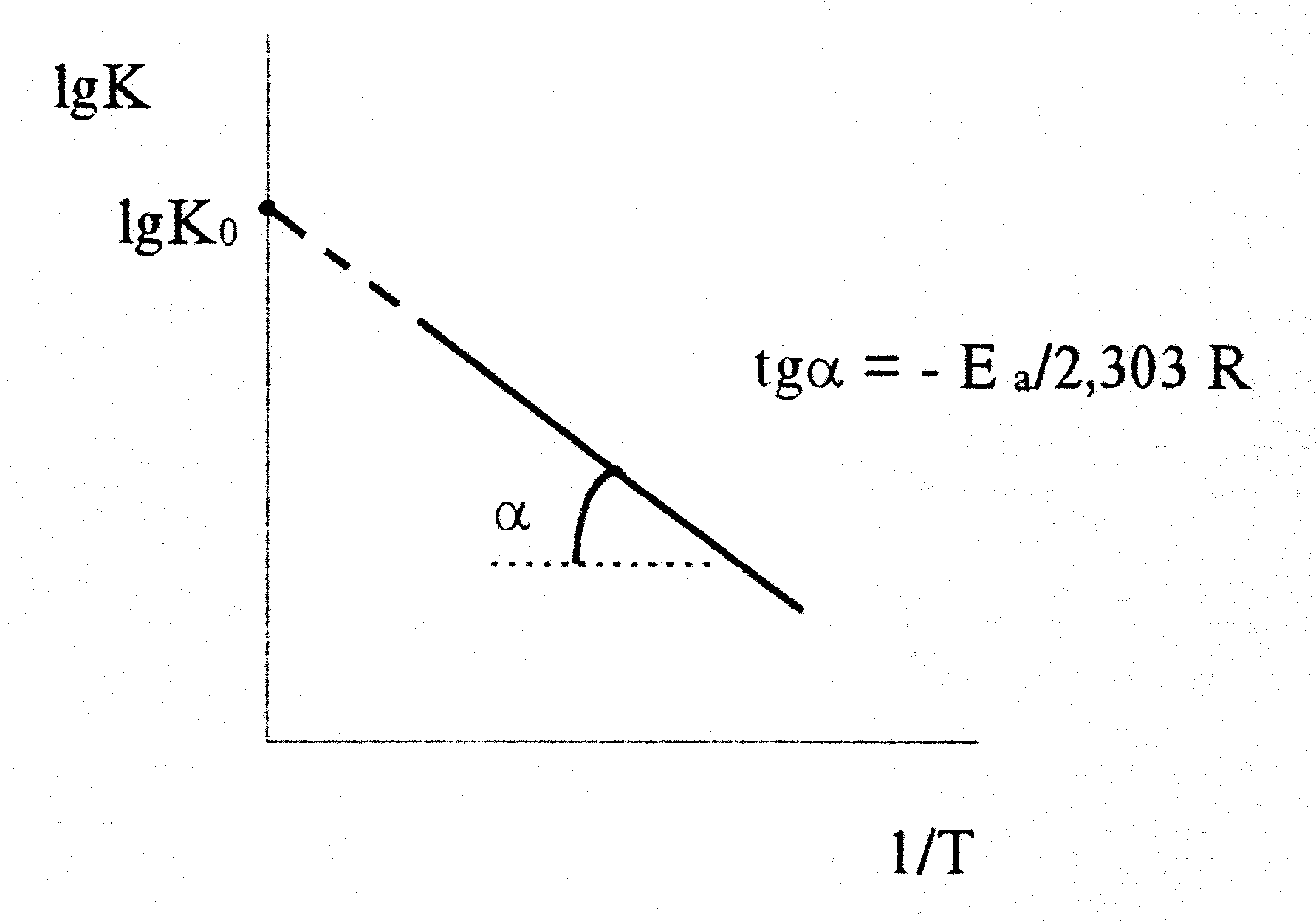Значение Е_а находят по тангенсу угла наклона прямой, проходящей через экспериментальные точки: Е _а= -2,303Rtgα.

Предэкспоненциальный множитель К₀ определяется от­резком, отсекаемым продолжением прямой на оси ординат при 1/Т = 0.

Если имеются значения константы скорости химической реакции при двух температурах, то из уравнения (9) можно полу­чить:

Е_а =(2,303RT₁T₂ lgK₂ /K₁ )/(T₂-T₁) (10)

Энергия активации Е_а имеет размерность энергия/моль и измеряется в единицах Дж/моль. Размерность К₀ совпадает с раз­мерностью константы скорости. Теория и экспериментальные данные (для широкого температурного интервала) показывают, что Е_а и К зависят от температуры. Однако эту зависимость мож­но не учитывать, если реакции исследуются в достаточно узком температурном интервале.

Изложенный выше метод расчета Е_а предполагает, что константы скорости реакций при различных температурах извест­ны.

Однако, есть способ расчета Е_а, так называемый метод трансформации, который не требует знания K=f(T).

Пусть при температурах T₁ и T₂ в смесях одного и того же начального состава протекает химическая реакция. Если к момен­там времени τ₁ и τ₂ реакция прошла на одну и ту же глубину, то есть изменения концентраций исходных веществ или продуктов реакции одинаковы, то отношение скоростей реакции равно:

W₁ / W₂ = (dC/d τ₁ ) /(dC/d τ₂) = d τ₂ / d τ₁. (11)

Заменим в уравнении (11) скорости реакций при заданных температурах соотношением

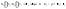. (11а)

Таким образом, отношение K₁ /K₂ можно заменить отно­шением τ₁ / τ₂

Подставим в отношение (11а) значения констант скорости при температурах T₁ и Т₂, используя уравнение Аррениуса:

K₀exp(-E_a/RT₁)/ K₀exp(-Ea/RT₂) = d τ₂ / d τ₁.

Полагая, что для узкого температурного интервала К₀ и Е_а= const находим

ехр[-Ea/R(l/T₁ - 1/Т2)] = d τ₂ / d τ₁. (12)

Разделение переменных и интегрирование дают:

ехр[-Еа(Т₂ – T₁ )/RT₁ T2 ] = τ₂ / τ₁. (13)

Следовательно, при заданных T₁ и Т₂ отношение τ₂ / τ₁ для реакций, протекающих на одну и ту же глубину, постоянно и называется коэффициентом трансформации. Если этот коэффици­ент известен, то значение энергии активации рассчитывается по формуле:

Е_а = R[T₁ T₂ /(Т₂ – T₁)]-ln(τ₂ / τ₁).