18) Уравнение Гиббса – Гельмгольца. Определение изменения энергии Гиббса реакции при не стандартной температуре.

Характеристической функцией называется термодинамическая функция, посредством которой или ее производных могут быть выражены в явном виде термодинамические свойства си-мы (p,V,T,S и др.).

Рассмотрим энергию Гиббса как функцию температуры и давления: G=f(T,p),

а энергию Гельмгольца как функцию температуры и объема: F=f(T,V).

Выразим полный дифференциал функции G и F через частные производные:

dG≤-SdT+Vdp (1)

dF≤-SdT-pdV (2)

dG=_PdT+_Tdp; (3)

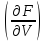dF=_VdT+_TdV. (4)

Сравнивая уравнения (1) с (3) и (2) с (4) для состояния равновесия си-мы, получаем

_P=-S; _T=V; (5)

_V=-S; _T=-p (6)

Т.о, частные производные энергии Гиббса по температуре и давлению и частные производные энергии Гельмгольца по температуре и объему равны параметрам S,V или p, т.е эти функции являются характеристическими функциями. Равенства (5) и (6) позволяют вывести ряд важных уравнений химической термодинамики. Приращение энергии Гиббса или энергии Гельмгольца выражается равенствами:

∆ G=∆H-T∆S; (7)

∆F=∆U-T∆S; (8)

Тогда соответственно из (5) и (6) вытекает

_P=-∆S; (9)

^V=-∆S; (10)

Подставляя выражения для ∆S из (9) и (10) в (7) и (8), получаем

∆ G=∆H+Т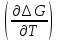_P; (11)

∆F=∆U+T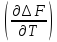_V; (12)

Уравнения (11) и (12) называются уравнениями Гиббса-Гельмгольца. Величины ∆ G и ∆F имеют смысл максимальной работы химической реакции, когда она проводится изотермически и обратимым путем, например в электрохимическом элементе.

Вторые слагаемые в правой части уравнений (11) и (12) имеют смысл теплоты обратимого процесса ,т.к

-Т_P=T∆S=Q_обр;

-Т_V=T∆S=Q_обр;

Величины ∆H и ∆U представляют собой тепловые эффекты химических реакций или физико-химических процессов, когда они осуществляются предельно необратимо. Уравнение Гиббса-Гельмгольца используются, например, для вычисления тепловых эффектов химических реакций по опытным значениям электродвижущих сил электрохимических элементов, для вычисления ∆S и других термодинамических величин.

19) Химический потенциал, определение, условие равновесия в открытых системах. Химический потенциал идеальных и реальных систем (газы, растворы).

При прохождении многих хим. процессов число молей компонентов в си-ме меняется, т.е количество компонентов в си-ме или в фазе могут быть переменными: n₁n₂n₃…….n_i

∆G=-S∆T+VdP+f(n₁)+f(n₂)+……f(n_i)

dG=f(T,P, n₁n₂n₃…….n_i)

dG=_P,nidT+ _T,nidP+_P,T,njdn₁+_P,T,njdn₂

где n_i-это постоянное количество всех компонентов в си-ме, n_j-это постоянное количество всех компонентов кроме одного изменение которого рассматривается.

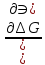_P,T,nj=ϻ_i

ϻ_i – химический потенциал i-го компонента.

ϻ_i – это частная производная в данном случае энергии Гиббса по массе итого компонента при постоянных р и Т и массах остальных компонентов.

ϻ_i – равно приращению энергии Гиббса при добавлении одного моля итого компонента к большому объему си-мы при постоянстве температуры и давления. Большой объем си-мы это когда состав си-мы почти не изменяется при добавлении 1моля компонента.

∂G= ϻ_i dn_i => G= ϻ_i

dG_T,P= ϻ₁ dn₁+ ϻ₂ dn₂+…. ϻ_i dn_i

dG_T,P=_P,T , если _P,T =0, то dG_T,P=0

это общее условие равновесие, при переменном числе компонента и постоянном р,Т.

dG_T,P≤0;=> _P,T ≤0

dU=TdS-pdV+ f(n₁)+f(n₂)+……f(n_i)

U= f(S,V, n₁n₂n₃…….n_i)

dU=_P,V,nidS+_SnidV+_S,V,njdn_j+ _S,V,njdn_i

dH=TdS+VdP+ f(n₁)+f(n₂)+……f(n_i)

H= f(S,P, n₁n₂n₃…….n_i)

dH=_P,nidS+_S,nidP+_S,P,njdn₁+_S,P,njdn_i.

dF=-SdT-pdV+ f(n₁)+f(n₂)+……f(n_i)

F=f(T,V,n₁n₂….n_i)

dF=_V,nidT+_T,nidV+_V,T,njdn1+_V,T,njdn_i.

dU=TdS-PdV+_idn_i

dH= TdS-VdP+_idn_i

dF= -SdT-PdV+_idn_i

dG= -SdT+VdP+_idn_i

выражает бесконечно малое изменение U,F,H,G для фазы масса которого может изменятся в результате обмена с др фазами.

ϻ_i=_S,V,nj

ϻ_i=_S,P,nj

ϻ_i=_T,V,nj

ϻ_i=_T,P,nj

Химический потенциал называется частные производные термодинамического потенциала по числу молей компонента при постоянстве естественных переменных и состава си-мы.

Химический потенциал идеального и реального газа.

∂G=-SdT+VdP

G=f(T,P)

T=const

dG=-SdT+VdP=VdP

PV=nRT => V=

dG=dP

G=nRTR_Ϭ, R_Ϭ-постоянная интегральная

G=RTLnP+ R_Ϭ (1)

G⁰=RTLnP⁰+ R_Ϭ (2)

Отнимем 1ур от 2го

G-G⁰=RT(LnP-LnP⁰) => G-G⁰=RTLn

P⁰=1атм => G-G⁰=RTLnP => G=G⁰+RTLnP

G=ϻ_i => ϻ_i = ϻ_i ⁰+RTLnP

Это ур для определения химического потенциала смеси идеального газа.

Льюис предложил для реальных газов использовать фугитивность( летучесть), т.к до сих пор рассматривались лишь такие си-мы газообразные части которых идеальны, т.е подчиняются уравнению PV=nRT для неидеальных систем все выше рассмотренные термодинамические соотношения не верны.

Предложенное Льюисом, остается в силе и для неидеальных систем, если заменить в них фактически парциальные давления эффективными давлениями(летучесть).

ϻ_i = ϻ_i ⁰+RTLnf, f-летучесть

Летучесть совпадает с давлением если последнее настолько мало, что газ становиться идеальным.

Фугитивностью(летучестью) назыв-ся величина, которую нужно подставить в выраж-е для хим-го потенциала идеального газа, чтобы получить значения реального газа.

ɣ==> ɣ- коэфф фугитивности , отношение фугитивности к давлению реального газа, т.е степень отклонения газов от идеального состояния.

ɣ_max=1, безразмерная величина.

Химический потенциал для идеального и реального растворов.

Для ид-го р-ра хим потенц: ϻ_i = ϻ_i ⁰+RTLnm_i (моляльная конц)

ϻ_i = ϻ_i ⁰+RTLnM(молярная конц)

ϻ_i = ϻ_i ⁰+RTLnX_i(мольная доля)

Активность итого компонента эта величина которую нужно подставить в ур для хим потенц компонента в идеальном растворе чтобы получить действительное значение хим потенциала итого компонента в неидеальном растворе.

ϻ_i = ϻ_i ⁰+RTLnа_i

ɣ==> a=ɣc

коэфф. Активности- отношение активности компонента в растворе к его концентрации.

a_x = ɣx_i Cx_i(мольные доли)

a_m= ɣm_i Cm_i(моляльность)

a_M= ɣM_i CM_i(молярность)