ММУ 530 2 задача

Вариант 530

n = 0, m = 3, l = 5

На трех базах А₁, А₂, А₃ находится однородный груз в количестве 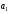, , 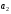 т соответственно. Этот груз необходимо развезти пяти потребителям В₁, В₂, В₃, В₄, В₅, потребности которых в данном грузе равны , , 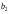, , 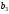 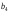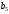т. Стоимость перевозок пропорциональна расстоянию и количеству перевозимого груза. Задана матрица тарифов – стоимости перевозки единицы груза от каждой базы каждому потребителю. Необходимо спланировать перевозки так, чтобы их общая стоимость была минимальной.

Потребители	В1	В2	В3	В4	В5	Запасы
Базы						(аi)
А1	5	8	15	20	9	225
А2	8	7	6	17	14	175
А3	11	11	19	10	5	200
Потребности (bj)	180	40	160	120	100	600

Решение:

Этап I. Поиск первого опорного плана.

Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

	1	2	3	4	5	Запасы
1	5[180]	8[25]	15	20[20]	9	225
2	8	7[15]	6[160]	17	14	175
3	11	11	19	10[100]	5[100]	200
Потребности	180	40	160	120	100

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 5*180 + 8*25 + 20*20 + 7*15 + 6*160 + 10*100 + 5*100 = 4065.

Этап II. Улучшение опорного плана.

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 5,

u₁+ v₂ = 8,

u₁+ v₄ = 20,

u₂+ v₂ = 7,

u₂+ v₃ = 6,

u₃+ v₄ = 10,

u₃+ v₅= 5.

	v1=5	v2=8	v3=7	v4=20	v5=15
u1=0	5[180]	8[25]	15	20[20]	9
u2=-1	8	7[15]	6[160]	17	14
u3=-10	11	11	19	10[100]	5[100]

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_i > c_ij

Выбираем максимальную оценку свободной клетки (1;5): 9

Проведем перестановку по циклу: 1,5; 1,4; 3,4; 3,5.

В результате получим новый опорный план.

	1	2	3	4	5	Запасы
1	5[180]	8[25]	15	20	9[20]	225
2	8	7[15]	6[160]	17	14	175
3	11	11	19	10[120]	5[80]	200
Потребности	180	40	160	120	100

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_i. по занятым клеткам таблицы, в которых u_i + v_i = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 5,

u₁+ v₂ = 8,

u₁+ v₅ = 9,

u₂+ v₂ = 7,

u₂+ v₃ = 6,

u₃+ v₄ = 10,

u₃+ v₅= 5.

	v1=5	v2=8	v3=7	v4=14	v5=9
u1=0	5[180]	8[25]	15	20	9[20]
u2=-1	8	7[15]	6[160]	17	14
u3=-4	11	11	19	10[120]	5[80]

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_i <= c_ij.

Минимальные затраты составят:

F(x) = 5*180 + 8*25 + 9*20 + 7*15 + 6*160 + 10*120 + 5*80 = 3945.