
Статистика КУРСАЧ отредактированный
.docxВ соответствии с вышеизложенным найдем частные производные (15):
 (15)
(15)
Сократив каждое уравнение на 2, раскрыв скобки и перенеся члены с и y в правую сторону, а остальные – оставив в левой, получим систему нормальных уравнений (16):
 (16)
(16)
где n – количество уровней ряда; t – порядковый номер в условном обозначении периода или момента времени; y – уровни эмпирического ряда.
Эта
система и, соответственно, расчет
параметров
 и
и
 упрощаются, если отсчет времени ведется
от середины ряда. Например, при нечетном
числе уровней серединная точка (год,
месяц) принимается за нуль. Тогда
предшествующие периоды обозначаются
соответственно –1, –2, –3 и т.д., а следующие
за средним (центральным) – соответственно
1, 2, 3 и т.д. При четном
числе уровней два серединных момента
(периода) времени обозначают –1 и +1, а
все последующие и предыдущие,
соответственно, через два интервала:
упрощаются, если отсчет времени ведется
от середины ряда. Например, при нечетном
числе уровней серединная точка (год,
месяц) принимается за нуль. Тогда
предшествующие периоды обозначаются
соответственно –1, –2, –3 и т.д., а следующие
за средним (центральным) – соответственно
1, 2, 3 и т.д. При четном
числе уровней два серединных момента
(периода) времени обозначают –1 и +1, а
все последующие и предыдущие,
соответственно, через два интервала:
 ,
,
 ,
,
 и т.д.
и т.д.
При
таком порядке отсчета времени (от
середины ряда)
 =
0, поэтому, система нормальных уравнений
упрощается до следующих двух уравнений,
каждое из которых решается самостоятельно
(17):
=
0, поэтому, система нормальных уравнений
упрощается до следующих двух уравнений,
каждое из которых решается самостоятельно
(17):
 (17)
(17)
Как
видим, при такой нумерации периодов
параметр
 представляет собой средний уровень
ряда. Определим по формуле параметры
уравнения прямой.
представляет собой средний уровень
ряда. Определим по формуле параметры
уравнения прямой.
Получаем,
что
 = 214,7/6 = 35,783 и
= 214,7/6 = 35,783 и
 = 9,5/28=0,339. Отсюда искомое уравнение тренда
= 9,5/28=0,339. Отсюда искомое уравнение тренда
 =35,783+
0,339t.
В 6-м столбце таблицы 4. приведены трендовые
уровни, рассчитанные по этому уравнению.
Для иллюстрации построим график
эмпирических (маркеры-кружочки) и
трендовых уровней.
=35,783+
0,339t.
В 6-м столбце таблицы 4. приведены трендовые
уровни, рассчитанные по этому уравнению.
Для иллюстрации построим график
эмпирических (маркеры-кружочки) и
трендовых уровней.
Для
каждого периода (каждой даты) определяются
теоретические уровни тренда ( )
и оценивается надежность
(адекватность) выбранной модели тренда.
Оценку надежности проводят с помощью
критерия Фишера, сравнивая его расчетное
значение Fр
(18)
с
теоретическими значениями FТ.
При этом расчетный критерий Фишера
определяется по формуле:
)
и оценивается надежность
(адекватность) выбранной модели тренда.
Оценку надежности проводят с помощью
критерия Фишера, сравнивая его расчетное
значение Fр
(18)
с
теоретическими значениями FТ.
При этом расчетный критерий Фишера
определяется по формуле:
 ,(18)
,(18)
где k – число параметров (членов) выбранного уравнения тренда; ДА – аналитическая дисперсия, определяемая по формуле ;; До – остаточная дисперсия Error: Reference source not found, определяемая как разность фактической дисперсии ДФ ; и аналитической дисперсии:
 ;
(19)
;
(19)
 ;
(20)
;
(20)
 (21)
(21)
Сравнение
расчетного и теоретического значений
критерия Фишера ведется обычно при
уровне значимости
 с учетом степеней свободы
с учетом степеней свободы
 и
и
 .
Уровень значимости
.
Уровень значимости
 связан с вероятностью
связан с вероятностью
 следующей
формулой
следующей
формулой
 .
При условии Fр
>
FТ
считается,
что выбранная математическая модель
ряда динамики адекватно отражает
обнаруженный в нем тренд.
.
При условии Fр
>
FТ
считается,
что выбранная математическая модель
ряда динамики адекватно отражает
обнаруженный в нем тренд.
Таблица 4. Вспомогательные расчеты для решения задачи
|
Год |
y |
t |
t2 |
yt |
|
(y
– |
( |
(y
–
|
|
2000 |
34,1 |
-3 |
9 |
-102,3 |
34,766 |
0,444 |
1,034 |
2,838 |
|
2001 |
35,2 |
-3 |
4 |
-70,4 |
35,105 |
0,009 |
0,460 |
0,340 |
|
2002 |
36,3 |
-1 |
1 |
-36,3 |
35,444 |
0,733 |
0,115 |
0,267 |
|
2003 |
36,5 |
-1 |
1 |
36,5 |
36,122 |
0,143 |
0,115 |
0,514 |
|
2004 |
35,8 |
2 |
4 |
71,6 |
36,461 |
0,437 |
0,460 |
0,000 |
|
2005 |
36,8 |
3 |
9 |
110,4 |
36,8 |
0 |
1,034 |
1,034 |
|
Итого |
214,7 |
0 |
28 |
9,5 |
214,7 |
1,766 |
3,218 |
4,987 |
Проверим
тренд в нашей задаче на адекватность
по формуле, для чего в 7-м столбце таблицы
4 рассчитан числитель остаточной
дисперсии, а в 8-м столбце – числитель
аналитической дисперсии. В формуле,
можно
использовать их числители, так как оба
они делятся на число уровней n
(n
сократятся): FР
=12,872/1,766=
7,289 >
FТ,
значит, модель адекватна и ее можно
использовать для прогнозирования (FТ=
7,71 находим по приложению 1 в 1-ом столбце
[ =
k
– 1 = 1]
и 8-й строке [
=
k
– 1 = 1]
и 8-й строке [ =
n
– k
= 4]).
=
n
– k
= 4]).
При составлении прогнозов уровней социально-экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза. Границы интервалов определяются по формуле (22):
 (22)
(22)
где
 –
точечный прогноз, рассчитанный по модели
тренда;
–
точечный прогноз, рассчитанный по модели
тренда;
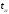 –
коэффициент
доверия по распределению Стьюдента
при уровне значимости
–
коэффициент
доверия по распределению Стьюдента
при уровне значимости
 и числе степеней свободы
и числе степеней свободы
 =n–1
(приложение 2);
=n–1
(приложение 2);
 – ошибка
аппроксимации,
определяемая по формуле Error: Reference source not found:
– ошибка
аппроксимации,
определяемая по формуле Error: Reference source not found:
 ,
(23)
,
(23)
где
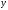 и
и
 –
соответственно фактические и теоретические
(трендовые) значения уровней ряда
динамики; n
–
число уровней ряда; k
–
число параметров (членов) в уравнении
тренда.
–
соответственно фактические и теоретические
(трендовые) значения уровней ряда
динамики; n
–
число уровней ряда; k
–
число параметров (членов) в уравнении
тренда.
Т.к. FР < FТ (7,289<7,71 ), то модель не адекватна и ее нельзя использовать для прогноза.


 )2
)2 –
– )2
)2 )2
)2