25) Языки программирования. Системы программирования.

Язык программирования — формальная знаковая система, предназначенная для записи компьютерных программ. Язык программирования определяет набор лексических, синтаксических и семантических правил, задающих внешний вид программы и действия, которые выполнит исполнитель (компьютер) под её управлением.

Семантика языка — это начальное смысловое значение операторов.

Система программирования — это система для разработки новых программ на конкретном языке программирования.

Состав системы программирования:

- языки программирования;

- служебные программы (редакторы, отладчики, оптимизаторы, интерпретаторы);

- информационное обеспечение (описания языков, служебных программ, модулей).

Системы быстрой разработки приложений (RAD) - упрощают и сокращают время разработки проекта. К таким системам относится Delphi. Например при добавлении какой-либо кнопки в проект система сама генерирует необходимый код и вставляет его куда нужно.

26) Понятие моделирования. Математическое моделирование.

Модель - упрощенный образ исследуемого объекта процесса или явления обладающий основными характеристиками свойствами исследуемого объекта оригинала, процесса или явления с точки зрения решаемые задачи.

Моделирование - разработка, создание, решение модели и применение результатов решения моделей.

Суть: изучение объекта оригинала заменяется изучением его модели, т.к. это проще.

Математическая модель – модель, в которой все взаимосвязи существующие между элементами моделей выражаются с помощью формул.

Модели классифицируются:

- материальные (модель самолета)

- физические (амперметр)

- идеальные (изображения)

Свойства математической модели:

- Достаточность - исходных данных должно быть достаточно для получения решения модели.

- Корректность

+ Существование решения

+ Единственность решения

+ Устойчивость решения - не должно быть больших погрешностей.

- Адекватность - результаты полученные по решению математической модели в достаточной степени точности согласуется с реальными данными.

27) Метод деления отрезка пополам

Задана непрерывная функция . Требуется определить корни уравнения.

1) находим отрезок , в котором расположено искомое значение корня, т.е.. 2) В качестве начального приближения корняпринимается середина этого отрезка, т.е.

3) Исследуем значение функции на концах отрезкови. Тот из них, на концах которого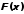принимает значения разных знаков, содержит искомый корень, его принимаем в качестве нового отрезка.

4) В качестве первой итерации корня принимаем середину нового отрезка и т. д.

5) Если , счет прекращается.

Function F(X)

F = X ^ 3...

End Function

Sub MDOP()

a = Cells(1, 2)

b = Cells(2, 2)

e = Cells(3, 2)

Do

X = (a + b) / 2

If F(a) * F(X) < 0 Then b = X Else a = X

Loop Until Abs(b - a) < e

Cells(4, 2) = X

Cells(5, 2) = F(X)

End Sub

28 Метод Ньютона

Суть: на -й итерации в точкестроится касательная к кривой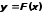и ищется точка пересечения касательной с осью абсцисс. Если задан интервал изоляции корня:, то за начальное приближениепринимается тот конец отрезка, на котором.

Уравнение касательной, проведенной к кривой в точкес координатамии, имеет вид:

Формула для -го приближения имеет вид:

Если 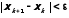счет прекращается.

Function F(x)

F = x ^ 3 ...

End Function

Function F1(x)

F1 = 3*x ^ 2 ...

End Function

Sub MH()

x = Cells(1, 2)

e = Cells(3, 2)

Do

x = x - F(x) / F1(x)

Loop Until Abs(F(x) / F1(x)) < e

Cells(4, 2) = x

Cells(5, 2) = F(x)

End Sub