32) Аппроксимация функций. Постановка задач и методы ее решения.

Очень часто в практической работе возникает необходимость найти в явном виде функциональную зависимость (формулу) между величинамии, которые заданы отдельными парами значений,(таблицей), например, полученными в результате измерений.

Аппроксимация - построение более простой зависимости, по известным характеристикам неизвестный зависимости.

Для получения единственного решения задачи аппроксимации необходимо

1. Задать общий вид аппроксимирующей функции, включающий неизвестные параметры. Вид функции задается, исходя из формы распределения аппроксимируемых значений, из предполагаемой функциональной зависимости, или просто в виде полинома некоторой степени;

2. Определить значения параметров на основе заданного критерия близости. Здесь существует два основных подхода – интерполяция и сглаживание(МНК).

Интерполяция.

Для задачи интерполяции критерий близости аппроксимирующей функции 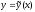к исходным данным,рассматривается как совпадение значений в заданных точках, называемых узлами интерполяции, т.е.

.

Если функция задана в виде полинома, то он называется интерполяционным полиномом и может быть записан, например, в форме Лагранжа или Ньютона.

33) Интерполяционные многочлены Лагранжа

Пусть на некотором промежутке заданыразличных узлов,,, …,, а также значения некоторой функции,,, …,в этих узлах. Необходимо построить полином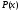, проходящий через заданные точки, т.е.

Интерполяционный полином Лагранжа имеет следующую формулу:

где

- фундаментальные полиномы Лагранжа. Они удовлетворяют равенствам

и зависят лишь от заданных узлов , но не от значений интерполируемой функции.

34) Интерполяционные многочлены Ньютона

Интерполяционный полином Ньютона имеет вид:

где

- разделенная разность первого порядка,

- разделенная разность второго порядка,

- разделенная разность третьего порядка и т.д.

35) Метод наименьших квадратов (МНК)

Аппроксимация на основе интерполяции не имеет смысла или невозможна, когда исходные данные содержат погрешности, повторы или очень большое количество точек. В этих случаях используют сглаживание: критерий близости аппроксимирующей функции к исходным данным,рассматривается как минимальное отклонение значений в заданных точках. Количественно отклонение может быть оценено методом наименьших квадратов (МНК), согласно которому необходимо минимизировать сумму квадратов:

где _, - значения данных - значение аппроксимирующей функции в точке;- число данных,- незвестные параметры. Задача сводится к нахождению экстремума функции параметров.

Линейная аппроксимация. В случае линейной формулы сумма квадратов принимает вид:

Эта ункция имеет минимум в точках, в которых частные производные от по параметрамиобращаются в нуль, т.е.

,

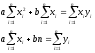
Решая систему уравнений, получим значения иуравнения.

Полиномиальная аппроксимация. В случае выбора зависимости в виде полинома, например, 2-й степени сумма квадратов принимает вид:

Эта функция имеет минимум в точках, в которых частные производные от по параметрам,,обращаются в нуль, т.е.:

, ,

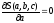В результате дифференцирования и элементарных преобразований для определения параметров получают систему из трех линейных уравнений с тремя неизвестными:

Или

При расчете удобно использовать таблицу

1	-2	6	4	-8	16	-12	24

Точность аппроксимации можно оценить среднеквадратической ошибкой

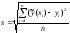, которая не должна превышать погрешность исходных данных.