Равновесие пространственной системы сходящихся сил
В
Три стержня
соединены в шарнире О.
Определить реакцию стержня СО,
возникающую под действием силы F
= 12 Н, приложенной к шарниру О,
если расстояния АВ
= АО
= АD.
(–
Н)
A
О
С
D
Три стержня
соединены в шарнире О.
Определить реакцию стержня ВО,
возникающую под действием силы F
= 2 кН, приложенной к шарниру О,
если расстояния АВ
= АО
= АD.
(
A
В
О
С
D
A
В
О
С
D
Три стержня
соединены в шарнире О.
Определить реакции стержней, если сила
F
= 2 кН приложена к шарниру О,
расстояния АВ
= ВС
= ОВ.
(S1
=
S2
= – 2 кН,
S3
=
А
В
С
D
К
Определить усилия
в тросе АВ
и в стержне АС
и АD,
поддерживающих груз Q
= 180 Н, если АВ
= 170 см, АС
= АD
= 100 см, CD
= 120 см; СК =
КD
и плоскость CDA
горизонтальна. (204 Н, – 60 Н)
1
2
3
кН)
кН)
30°
А
В
С
D
E
К вершине В
треножника АВСD
подвешен груз Е,
вес которого 100 Н. Ножки имеют равную
длину, укреплены на горизонтальном
полу и образуют между собой равные
углы. Определить усилие в каждой из
ножек. (38.49 Н) 
Равновесие произвольной пространственной с Kистемы сил
Однородная плита
весом G
= 400 H
может вращаться вокруг горизонтальной
оси АВ
на петлях А
и В,
и удерживается в горизонтальном
положении тросами СЕ
и DK.
Определить натяжения тросов.
(200 Н)
А
30°
D
E
В
30°
С
А
В
D
Е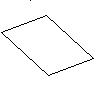
Однородная плита
весом G
= 500 H
может вращаться вокруг горизонтальной
оси АВ
на петлях А
и В,
и удерживается в горизонтальном
положении тросом DЕ.
Определить натяжение троса и реакции
петель А
и В.
(T
= 500 Н, XA
=
z
H,
ZA
= XB
= 0, ZB
= 250 H)
30°
х
y
С
30°
В
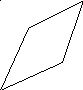
Однородная
прямоугольная крышка веса G
= 200 Н удерживается при открытой на 30°
над горизонтом стержнем DE.
Определить усилие в стержне DE
и реакции шарниров А
и В.
(S
=100 Н, XA
= 50 H,
ZA
=
H,
XB
= 0, ZB
= 100 H)
D
y
z
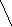
A
E
х
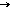
y
z
30°
30°
A C D
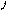
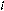
Однородная
прямоугольная рама веса 200 Н удерживается
шаровым шарниром А,
петли В
и веревкой. Определить натяжение веревки
и опорные реакции. (Т
= 200 Н, XA
= 86.6 H,
YA
=150
H,
ZA
= 100
H, XB
= ZB
=100 H)
В
x
Однородная
прямоугольная крышка веса G
= 400 Н удерживается при открытой на 30°
над горизонтом противовесом Q.
Определить вес Q
и реакции шарниров А
и В,
если блок E
укреплен на одной вертикали с А
и АЕ
= АС.
(Q
= 200 Н, XB
= 0, ZB
= 200
H, XA
=173.21
H,
ZA
= 100
H)
у z
В
E
С Q
A
30°
х
К коленчатому
валу АВ
под углом
= 60° к горизонту приложена сила F
= 10 Н, которая уравновешивается парой
сил с моментом М.
Определить модуль момента, если сила
А
В
y
х
z
M
b
Груз Q
= 100 Н
равномерно поднимается мотором М.
Определить реакции опор А
и В
и натяжения в цепи, если нижняя ветвь
цепи наклонена к горизонту под углом
30°. Известно, что r
= 10 см, R
= 20 см, натяжение ведущей части цепи
вдвое больше натяжения ведомой части,
т.е. Т1
= 2Т2.
(Т1
= 50 Н, Т2
= 25 Н,
ХА
= 27.3
Н, ZA
= 60 H,
ХВ
=
41 Н, ZB
= 15 H)
А
В
y
M
30°
30см
30см
r
R
С помощью ворота,
удерживается груз Q
= 1 кН. Радиус барабана R
= 10 см, длина рукоятки KD
= 50 см, AD
= 30 см, AC
= 40 см, СВ
= 40 см. Веревка сходит с барабана по
касательной, наклоненной к горизонту
под углом 60°. Определить давление P
на рукоятку и реакции опор А
и В
при том положении ворота, когда рукоятка
KD
горизонтальна. (Р
= 0.2 кН, ХА
=
0.25 кН, ZA
= – 0.16 кH,
ХВ
=
0.25 кН, ZB
= 0.51 кH)
||Oxz
и b
= 0.9 м (7.79 Нм)
С помощью ворота,
удерживается груз Q
= 1 кН. Радиус барабана R
= 10 см. Длина рукоятки KD
= 50 см, AD
= 30 см, AC
= 40 см, СВ
= 40 см. Веревка сходит с барабана по
горизонтали. Определить давление P
на рукоятку и реакции опор А
и В
при горизонталь-ном положении рукоятки
KD.
(Р
= 200 Н, ХА
= ХB
= – 500 H,
ZA
= 275 H,
ZB
= – 75 H)
K
D
R
С
х
z
y
В
А
Q
40см
z
х
Q
60°
y
Q
В
С
z
R
А
K
D
х
Пример 1.
Положение точки А
в пространстве определяется радиус-вектором
(м)
.
К точке А
приложена
сила (Н)
.
Определить модуль момента этой силы
относительно начала координат О.
Решение. Вектор момента силы F, приложенная в точке А, относительно центра О определяется как
,
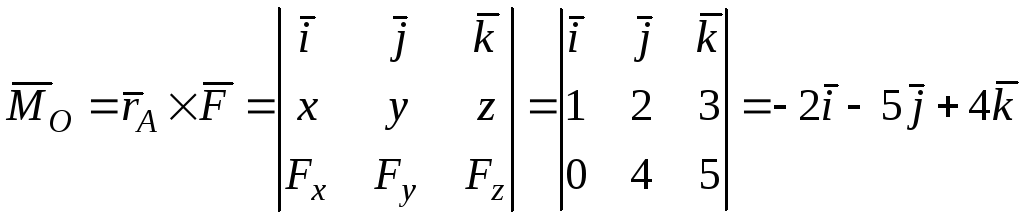где
Нм,
Нм,
Нм
– проекции
на оси координат.
Модуль момента
Нм.
Ответ:
Нм.
Пример 2. Три стержня соединены в шарнире О. Определить реакции стержней, если к шарниру О приложена сила F = 1 кН. Расстояния принимать АВ = ВО = СD (рис. 1, а).
Решение. Воспользуемся способом вырезания узлов. Все стержни фермы условимся считать растянутыми; знак минус у вычисленной реакции стержня покажет, что стержень сжат (рис. 1, б).
а)
б)
В
А
О
С
А
В
y
z
Рис. 1
D
D
О
С
x
Составляя три уравнения равновесия сил действующих на узел О, получаем:
:
;
:
;
;
:
;
кН;
Из второго уравнения
кН,
из первого
кН.
Знак плюс в ответе указывает на то, что истинное направление совпадает с направлением, указанным на схеме (рис. 1, б).
Ответ:
,
и
Пример 3. Рабочий поднимает груз Q = 500 Н с помочью ворота; радиус барабана r = 10 см, длина рукоятки АК = 50 см, АС = СВ = 50 см. Определить давление F на рукоятку и реакции узлов А и В, если рукоятка AK находится в горизонтальном положении (рис. 2, а).
В
y
Q
C
r
60°
В
Q
C
r
60°
а)
б)
F1
F1
F1
F1
y
z
z
К
А
х
К
А
х
Рис. 2
Решение.
Изобразим действующие на ворот силы:
сила F,
натяжение веревки Q,
по модулю равное весу груза, и составляющие
,
,
,
реакции подшипников.
Определим силу F из уравнения моментов сил относительно оси АВ:
:
;
Н.
Составляющие
,
найдем, рассматривая уравнения моментов
относительно осейАz
и Аx
соответственно.
:
;
Н.
:
;
Н.
Составляющие
,
найдем из следующих уравнений:
:
Н.
:
Н.
Ответ:
Н,
Н,
Н,
Н,
Н.