
С1_0
.doc
45°
В

1 м
qmax=4
кН/м
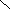
А
В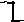

А
30°
45°
3
кН
А 4
м
5
кНм
Определить реакции
заделки А
консоль-ной балки, находящейся под
действием сосредоточенной силы и пары
сил.
(XA=
2.12 кH;
YA=
2.12 кH;
mА=
3.49 кH·м)
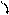














В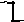
А 2
м
2
кН 2
м
Определить реакции
заделки А
консоль-ной балки, находящейся под
действием сосредоточенной силы и
равномерно распределенной нагрузки.
(YA
= 4
кH; mА=
– 2 кH·м)
q=3
кН/м






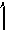














В
6
кН
А
В 3
м
qmax=4
кН/м
2
м
Определить момент
в заделке А
балки, находящейся под действием
сосредоточен-ной силы и распределенной
нагрузки, изме-няющейся по закону
треугольника. (42кHм)























А
В 3
м
q=2 кН/м
2
м
3 кНм
q=3
кН/м
60°
1 м
4
м
6 кН
Определить момент
в заделке А
консольной балки, находящейся под
действием пары сил и равномерно
распределенной нагрузки. (13 кH·м)
А
С D
2
м 2
м
10 кН
1
м
60°
А
С
В D
3
м
Балка АВ
удерживается в горизонталь-ном положении
вертикальным стержнем CD.
Определить усилие в стержне CD.
(20 кH)
Балка АВ
удерживается в горизонталь-ном положении
стержнем CD.
Определить вертикальную составляющую
реакции в шарнире А.
(4 кH)
Определить реакции
заделки В
консольной балки, находящейся под
действием равномерно распределенной
нагрузки и сосредоточенной силы.
(XВ
= 3 кH; YВ
= 5.2 кH; mВ
= 41.2 кH·м)


































































А
В
В








4
кНм










2
м
4 кН
А
В D
2
м 2
м
4 кН
1
м
2
кН
Балка АВ
удерживается в горизонталь-ном положении
вертикальным стержнем CD.
Определить усилие в стержне CD.
(3кH)









С
30°
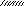
А
С
В
2
м 2
м
4
кН
1
м D
q=2 кН/м
А
С
В D 2
м
5
кН
1
м
45°
8
кН 2
м
45° C
В
Балка АВ
удерживается в горизонталь-ном положении
стержнем CD.
Определить усилие в стержне CD.
(41.57 кH)
Балка АВ
удерживается в горизонталь-ном положении
стержнем CD.
Определить усилие S
в стержне CD.
(42.43 кH)
Однородная балка
АВ,
весом 10 кН, опирается на гладкую
вертикальную стену. Определить реакцию
стенки. (17.32 кH)
Однородная балка
АВ весом
30 кН опирается о выступ в точке С.
Найти силы давления балки на опору В,
если АС
= 1/4АВ.
(XВ
= –10 кH; YВ
= 20 кH)







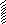
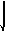



























































60°
В
А









![]()








60°
А
В
30°
Однородная балка
АВ
весом 52 кН опирается о выступ С.
Определить реакцию выступа, если ВС
= 1/4АВ.
(30 кH)
С




















А
Пример 1. Один конец стержня АВ закреплен шарнирно в точке А. К другому концу В привязан груз весом 50 Н. Стержень удерживается в равновесии веревкой ВС. Определить реакцию веревки ВС и стержня АВ, если угол = 30° (рис. 1, а).
Решение. Покажем на схеме (рис. 1, б) все силы приложенные к узлу В. Направим все реакции от узла. Ответ со знаком минус укажет, что стержень АВ не растянут, а сжат. Для сил приложенных к узлу В составим уравнение равновесия сходящихся сил, расположенных в плоскости.
С
В
С
В
а)
б)



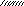








![]()


y
![]()
х

![]()
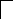
А
А
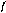
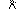
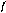
Рис. 1
![]() :
:
![]() ;
;
![]()
![]() .
.
![]() :
:
![]()
![]()
![]() H.
H.
Подставляя найденное
натяжение веревки Т
в первое уравнение, определяем реакцию
стержня
![]() Н
(стержень растянут).
Н
(стержень растянут).
Ответ:
![]() Н,
Н,
![]() Н.
Н.
Пример 2.
Определить реакции опор А
и C
балки АВ,
находящейся под действием двух
сосредоточенных сил
![]()
![]() и пары сил с моментом
и пары сил с моментом
![]() .
(рис. 2, а).
.
(рис. 2, а).
Решение. Мысленно отбрасываем связи: шарнирно-неподвижную опору А и опору на катках С, – заменяя их действие соответствующими реакциями (рис. 2, б).
а)
б)
А 2
м
1 м

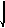
![]()

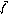
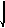


![]() F1
F1![]()
![]()
![]()
45° M
45° M
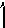
![]() F1
F1
В
А
В C







![]()
