- •Раздел 3. Центральное растяжение (сжатие)
- •Напряжения в наклонных сечениях бруса
- •Статически неопределимые задачи растяжения (сжатия)
- •II. Определить усилия в стержнях плоской шарнирно-стержневой системы, состоящей из трех стержней, нижние концы которых соединены общим шарниром и загружены в нем вертикальной силой (рис. 3.10).
- •III. Бесконечно жесткий брус ав шарнирно прикреплен к неподвижной опоре, подвешен на трех стержнях и нагружен силой (рис. 3.11). Определить усилия в стержнях?
- •IV. Определение монтажных напряжений
- •V. Определение температурных напряжений
- •Общий случай статически-неопределимых задач растяжения (сжатия).
- •Механические свойства материалов
- •Метод разрушающих нагрузок (р.Н)
- •Энергия деформации
Раздел 3. Центральное растяжение (сжатие)
Центральным
растяжением (сжатием) называется
такой вид деформации, при котором в
поперечном сечении бруса возникает
только продольная
сила![]() .
.
Растяжение (сжатие) часто встречается в элементах строительных конструкций и машин. Например, растяжение возникает в тросе подъемника, сжатие – в фабричной трубе от собственного веса, в колоннах и т.д.
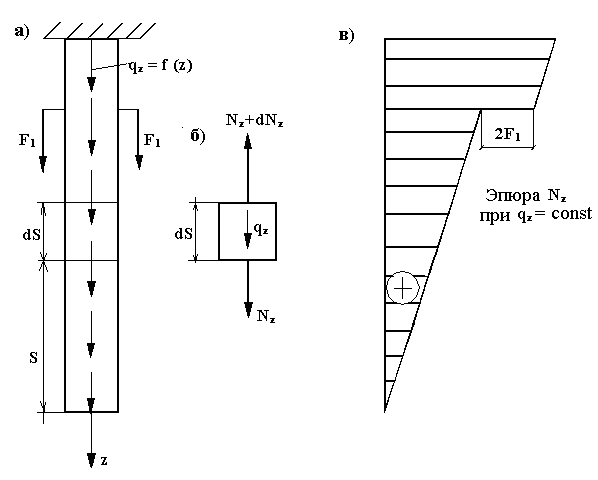
Для центрального растяжения (сжатия) внешние силы, приложенные к концевым или промежуточным сечениям стержня, должны быть направлены по его оси или приводиться к равнодействующей, направленной по этой оси (рис. 3.1а).
Для определения
продольных сил применяется метод
сечений. При
этом стержень мысленно рассекается
плоскостью, перпендикулярной оси
стержня, на две части. Взаимодействие
частей между собой заменяется продольной
силой
![]() и из условия равновесия
и из условия равновесия
![]() отсеченной части определяется значение
этой силы (рис. 3.1 б-г).
отсеченной части определяется значение
этой силы (рис. 3.1 б-г).
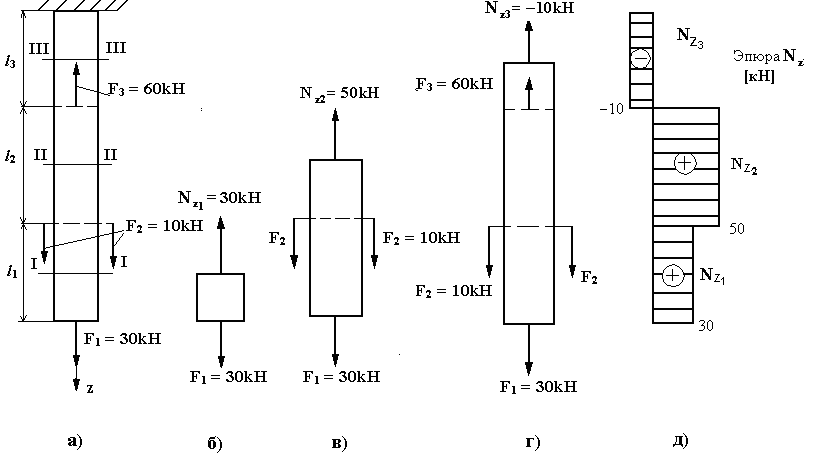
Рис.3.1
Условимся силу
![]() считать положительной, если она вызывает
растяжение (направлена от сечения) и
отрицательной, если вызывает сжатие
(направлена к сечению). В тех случаях,
когда направление силы
считать положительной, если она вызывает
растяжение (направлена от сечения) и
отрицательной, если вызывает сжатие
(направлена к сечению). В тех случаях,
когда направление силы
![]() неизвестно, целесообразно принять ее
положительной. Если из условия равновесия
сила
неизвестно, целесообразно принять ее
положительной. Если из условия равновесия
сила
![]() получиться со знаком (+), то стержень в
данном сечении растянут, если со знаком
(–), то – сжат.
получиться со знаком (+), то стержень в
данном сечении растянут, если со знаком
(–), то – сжат.
В сложных случаях
нагружения стержня целесообразно
строить эпюру внутренних сил. Эпюрой
продольной силы
![]() называется график, каждая ордината
которого равна значению продольной
силы в данном сечении. Этот график
показывает изменение продольных сил
по длине оси бруса. Для этого проводим
базисную линию, параллельную оси стержня
(рис. 3.1д), и перпендикулярно к ней отложим
отрезки, изображающие в некотором
масштабе величины продольных сил
называется график, каждая ордината
которого равна значению продольной
силы в данном сечении. Этот график
показывает изменение продольных сил
по длине оси бруса. Для этого проводим
базисную линию, параллельную оси стержня
(рис. 3.1д), и перпендикулярно к ней отложим
отрезки, изображающие в некотором
масштабе величины продольных сил
![]() в поперечных сечениях бруса.
в поперечных сечениях бруса.
Очевидно, что на
всем участке длиной
![]() (между точками приложения сил
(между точками приложения сил
![]() и
и
![]() )
продольная сила постоянна и равна
)
продольная сила постоянна и равна
![]() ;
аналогично и на других участках (между
сечениями, в которых приложены внешние
силы), продольные силы имеют постоянное
значение.
;
аналогично и на других участках (между
сечениями, в которых приложены внешние
силы), продольные силы имеют постоянное
значение.
В поперечных
сечениях, в которых к брусу приложены
сосредоточенные продольные силы,
значение продольной силы
![]() изменяется скачкообразно
на величину продольной силы.
изменяется скачкообразно
на величину продольной силы.
При действии на
брус внешней распределенной осевой
нагрузки
![]() продольные силы
продольные силы
![]() на участке, на котором такая нагрузка
приложена, изменяются непрерывно (рис.
3.2).
на участке, на котором такая нагрузка
приложена, изменяются непрерывно (рис.
3.2).
|
Рис.3.2 |
Природа внешней распреде-ленной осевой нагрузки может быть различной. Обычно это собственный вес или инерцион-ные силы.
Для решения этой
задачи рассмотрим равновесие бесконе-чно
малого элемента, вырезанно-го двумя
сечениями, располо-женными друг от
друга на расстоянии
|
нюю силу
![]() ,а
к верхнему – силу
,а
к верхнему – силу
![]() .
Из условия равновесия этого элемента
находим
.
Из условия равновесия этого элемента
находим
![]() .
Отсюда следует
.
Отсюда следует
![]() (3.1)
(3.1)
т.е. величина нормальной силы в произвольном сечении равна сумме проекций на ось стержня всех внешних сил (интегралу), приложенных к отсеченной части.
На рис. 3.2 в показана
эпюра
![]() для бруса (рис. 3.2а) при
для бруса (рис. 3.2а) при
![]() .
.
Все вышесказанные
правила построения эпюр
![]() можно свести к простым практическим
приемам. Для определения
можно свести к простым практическим
приемам. Для определения
![]() в любом сечении стержня (колонн),
используем метод
сечений и
формулы (1.5) полученные в разделе 1.
в любом сечении стержня (колонн),
используем метод
сечений и
формулы (1.5) полученные в разделе 1.
![]() (А)
(А)
При наличии погонной
нагрузки
![]() учитываются и формулы (3.1).
учитываются и формулы (3.1).
Для горизонтальных
стержней ось
![]() будем направлять слева направо. Для
вертикальных стержней (колонн), ось
будем направлять слева направо. Для
вертикальных стержней (колонн), ось
![]() будем направлять вниз и за правую
отсеченную часть будем считать нижнюю
от разреза часть, а за левую – верхнюю.
Все внешние нагрузки, направленые вдоль
оси
будем направлять вниз и за правую
отсеченную часть будем считать нижнюю
от разреза часть, а за левую – верхнюю.
Все внешние нагрузки, направленые вдоль
оси
![]() ,
считаем положительными. Построим эпюру
,
считаем положительными. Построим эпюру
![]() для колонны, показанной на рис. 3.3.
для колонны, показанной на рис. 3.3.
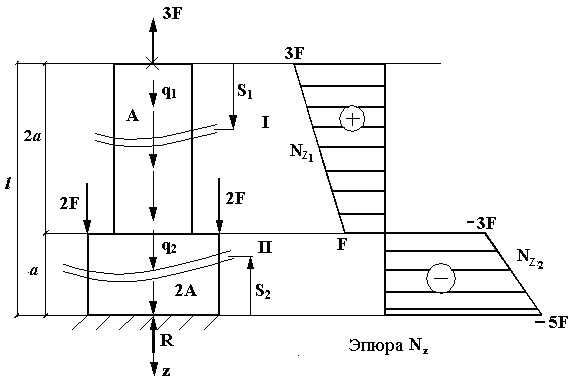
Рис.3.3
Площадь верхней
части колонны А,
площадь поперечного сечения нижней
части 2А.
Oбозначим
![]() – объемный вес материала колонны. Тогда
погонные нагрузки от веса будут
– объемный вес материала колонны. Тогда
погонные нагрузки от веса будут
![]() .
R
– опорная реакция. Для простоты вычислений
свяжем силы
.
R
– опорная реакция. Для простоты вычислений
свяжем силы
![]() и нагрузки от веса формулой
и нагрузки от веса формулой
![]() (В)
(В)
Найдем опорную
реакцию
![]() из условия равновесия всей колонны
из условия равновесия всей колонны
![]() .
.
![]()
С учетом (В) найдем
![]() .
.
Колонна имеет два участка.
I
участок
(верхний). Проведем в нем сечение на
расстоянии
![]() от верхнего торца колонны,
от верхнего торца колонны,
![]() ,
т.е. рассмотрим верхнюю часть от разреза,
что как указано выше, надо в формулах
(А) считать «левой» частью
,
т.е. рассмотрим верхнюю часть от разреза,
что как указано выше, надо в формулах
(А) считать «левой» частью
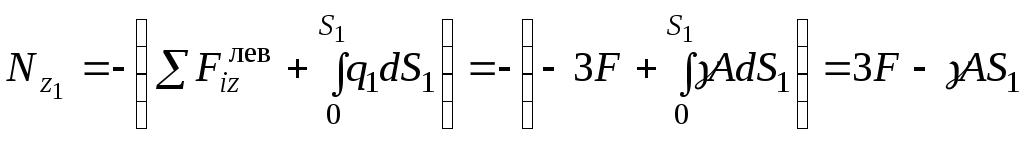
Эпюра
![]() линейна, т.к.
линейна, т.к.
![]() в первой степени. Для построения эпюры
надо две точки:
в первой степени. Для построения эпюры
надо две точки:
![]()
В масштабе
откладываем эти величины на эпюре
![]() .
.
II
участок.
Проведем в нем разрез на расстоянии
![]() от опоры,
от опоры,
![]() и эту нижнюю часть в формулах (А) считаем
«правой»
и эту нижнюю часть в формулах (А) считаем
«правой»
![]()
Для построения эпюры достаточно двух точек
![]()
Здесь и на I
участке использована зависимость (В).
Строим эпюру
![]() .
Верхний участок колонны растянут, а
нижний сжат. Скачки
.
Верхний участок колонны растянут, а
нижний сжат. Скачки
![]() должны быть равны силам, приложенным к
колонне в этих сечениях.
должны быть равны силам, приложенным к
колонне в этих сечениях.
Напряжения и деформации при растяжении (сжатии).
Закон Гука.
Продольная сила
![]() ,
возникающая в поперечном сечении бруса,
представляет собой равнодействующую
внутренних нормальных напряжений
,
возникающая в поперечном сечении бруса,
представляет собой равнодействующую
внутренних нормальных напряжений
![]() ,
распределенных по площади поперечного
сечения и связаны известной зависимостью
(1.6):
,
распределенных по площади поперечного
сечения и связаны известной зависимостью
(1.6):
![]() (3.2)
(3.2)
Здесь
![]() представляет собой элементарную
внутреннюю силу, приходящуюся на площадку
представляет собой элементарную
внутреннюю силу, приходящуюся на площадку
![]() .
.
Как уже отмечалось
выше, величину
![]() в каждом случае легко можно определить
при помощи метода
сечений.
Однако из формулы (3.2) нельзя найти закон
распределения нормальных напряжений
в каждом случае легко можно определить
при помощи метода
сечений.
Однако из формулы (3.2) нельзя найти закон
распределения нормальных напряжений
![]() по площади поперечного сечения.
по площади поперечного сечения.
Опыты показывают, что если нанести на поверхность бруса систему линий, перпендикулярных к его оси, то после нагружения стержня поперечные линии переместятся параллельно самим себе. Значит, если мысленно представить себе брус состоящим из тонких продольных призматических элементов (волокон), то все поверхностные элементы будут удлиняться одинаково. Естественно предположить, что и внутренние продольные элементы тоже удлиняются одинаково, т.е. поперечные сечения смещаются параллельно начальным положениям, что соответствует гипотезе плоских сечений (гипотезе Бернулли).
Согласно этой гипотезе сечения, плоские до деформации, остаются плоскими и после деформации.
Так как одинаковым
удлинениям в однородном материале
соответствуют одинаковые напряжения,
то напряжения в поперечных сечениях
всех призматических элементов (волокон),
а следовательно, и во всех точках
поперечного сечения бруса, равны между
собой. Это позволяет в (3.2) вынести
величину
![]() за знак интеграла. Тогда
за знак интеграла. Тогда
![]() (3.3)
(3.3)
Итак, в поперечных сечениях бруса при центральном растяжении или сжатии возникают равномерно распределенные нормальные напряжения, равные отношению продольной силы к площади поперечного сечения.