Определение деформации балок при изгибе

Прогиб и поворот сечения балки

При действии внешних сил, расположенных в одной из главных плоскостей инерции сечения балки, наблюдается искривление ее оси в той же плоскости, происходит плоский изгиб.

На рис. изображена искривленная ось балки в плоскости , защемленной одним концом и нагруженной на другом конце силой. Центр тяжестиС какого-либо сечения с абсциссой при дефор-мации балки переместится в т..

Перемещение ц.т. сечения по направлению, перпендикулярному к оси балки, называетсяпрогибом балки в этом сечении. Прогиб обозначается буквой .

=

При деформации балки сечение поворачивается на некоторый угол , который называетсяуглом поворота сечения.

Обе величины, определяющие деформации балки, являются функцией от .

Уравнение представляет собой уравнение кривой, по которой изогнется ось балки, это будетуравнение изогнутой оси балки.

Касательная к изогнутой оси балки в т. составит с осьюугол, равный. С другой стороны, тангенс угла, образованного касательной к кривойи осью, как известно, равен

Так как на практике прогибы балки обычно малы по сравнению с длиной балки, то углы малы.

Для таких углов можно считать, что тангенс угла равен самому углу, выраженному в радианах. Следовательно

(5.19)

При выбранных нами направлениях координатных осей (см. рис) положительный прогиб будет вниз, а положительный угол поворота сечения – по направлению вращения часовой стрелки.

Дифференциальное уравнение изогнутой оси балки

Для получения зависимости надо установить, как зависят деформации балки от внешних сил, изгибающих ее, от размеров и материала балки.

Такая зависимость была получена нами ранее при выводе формулы нормальных напряжений при изгибе в виде связи кривизны оси балки с изгибающим моментом (5.11):

(а)

где радиус кривизны изогнутой оси балки.

Однако в общем случае использовать зависимость (а) для определения прогибов не удается.

С другой стороны, из курса высшей математики известна зависимость между радиусом кривизны плоской кривой и координатами иее точек:

(б)

Приравнивая выражения (а) и (б) исключим радиус кривизны:

(в)

Это дифференциальное уравнение изогнутой оси, или дифференциальное уравнение упругой линии.

Выше мы уже отмечали, что – величины очень малые, поэтому их квадратом можно пренебречь по сравнению с единицей. Тогда уравнение (в) упростится

(г)

Это приближенное дифференциальное уравнение изогнутой оси. Правило знаков для изгибающего момента установлено ранее.

Знак в формуле (г) зависит от выбора направлений осей координат. В нашем случае, когда ось горизонтальна и направлена вправо, а осьвниз, надо брать знак «–». Итак

(5.20)

Если ось у направлена вверх, надо взять знак «+».

Интегрирование дифференциального уравнения упругой линии

Для того, чтобы получить аналитические выражения для прогибов и углов поворота необходимо найти решение дифференциального уравнения (5.20). Правая часть уравнения является известной функцией для каждой конкретной балки с конкретным загружением. Интегрируя его один раз, получим:

Это выражение определяет закон изменения углов поворота сечений балки.

После повторного интегрирования найдем уравнение оси балки

Постоянные интегрирования С и D находятся из граничных условий.

Уравнения (5.20) записываются для каждого участка балки и интегрируются. При большом числе участков определение const иосложняется, т.к. приходится решать большое число совместных алгебраических уравнений, из которых они вычисляются. Поэтому для таких балок были разработаны другие методы.

Один из таких методов сводится к уравниванию однотипных const интегрирования, для чего, при составлении аналитических выражений изгибающих моментов по участкам балки, необходимо соблюдать ряд условий.

Метод уравнивания произвольных постоянных

(метод Клебша)

Равенство между собой произвольных постоянных (и) при большом числе участков балки возможно при соблюдении следующих условий:

1. Отсчет координат всех участков должен вестись от одного конца балки.

2. Все составляющие выражения 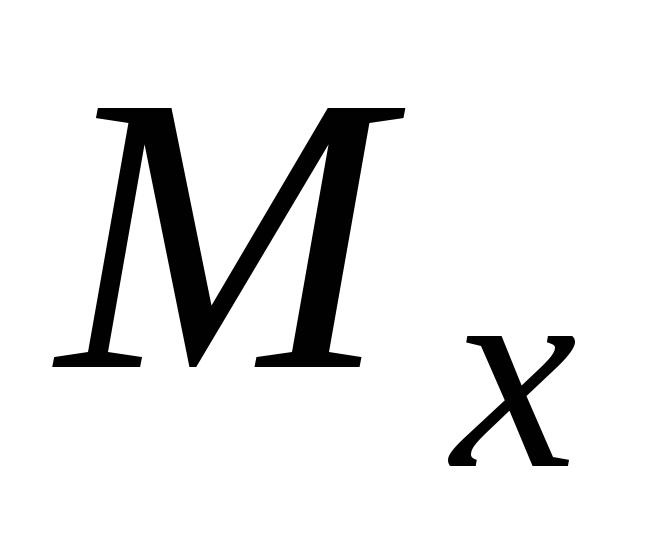предыдущего участка, должны сохраняться неизменными в выраженияхпоследующего участка. Поэтому, если на каком-то участке появляется распределенная нагрузка, не идущая до конца балки, то ее надо продлить до конца балки, добавив на этих же участках такую же распределенную нагрузку с противоположном знаком.

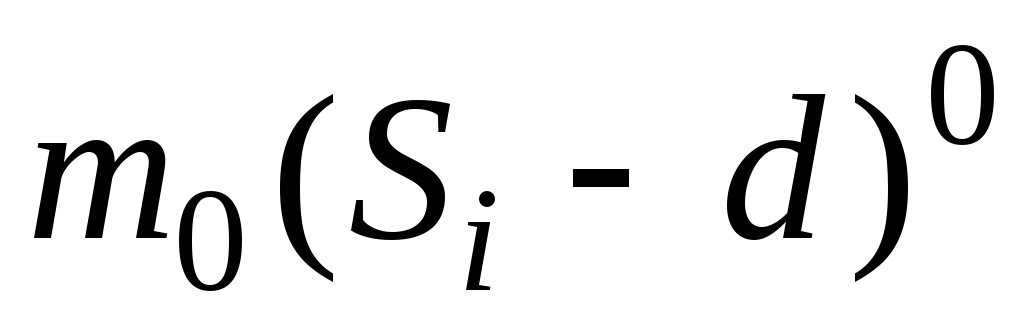3. Сосредоточенные моменты вводятся в виде, гдерасстояние от начала балки до сечения, где приложены.

4. Интегрирование дифференциальных уравнений должно вестись без раскрытия скобок.

Поясним выполнение перечисленных условий на примере:

Пример (рис.5.11):

Дано: 1,5м;4,5м;4м;20кН;45кН/м;20кНм;кН/см²; =16кН/см²; =10кН/см²;

Рис.5.11

На рис. 5.11 сплошными линиями и перечеркнутыми показаны нагрузки заданные, а пунктиром показаны добавки нагрузоксогласно п.2 метода Клебша. Сначала учитываем только заданные нагрузки. По правилам, показанным при решении примера 1 на рис. 5.5, находим:

1. Из уравнений равновесия всей балки при заданных нагрузках находим все опорные реакции: 154,12кН; 84,12кН;.

2. Строим эпюру 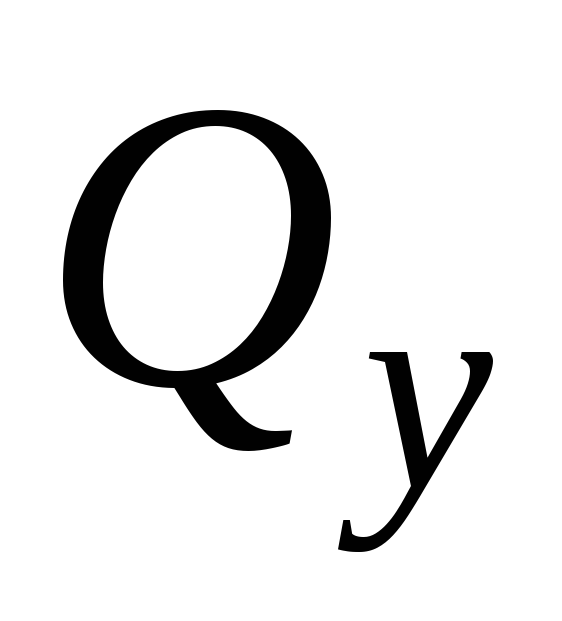и эпюру, из которых находим105,68кНм и 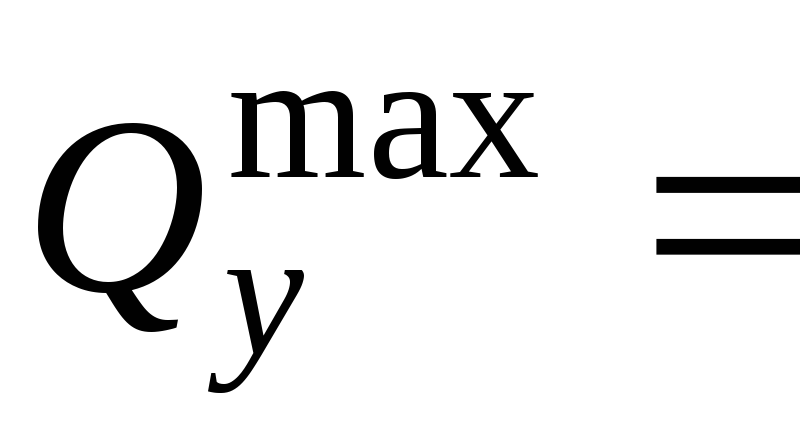106,62кН

Для балки подберем стандартный двутавр:

Из условия прочности балки (5.17) находим