
6____2004
.pdf
Уравнение плоскости, проходящей через точку P , имеет вид
α : A(x − x1 ) + B( y − y1 ) +C(z − z1 ) = 0 ;
эта плоскость должна быть перепендикулярна к прямой l . По условию перпендикулярности прямой и плоскости
mA = Bn = Cp ;
выбирая для простоты множитель пропорциональности, равный единице, находим A = m, B = n, C = p .
Итак, уравнение плоскости α будет иметь вид
m(x − x1 ) + n( y − y1 ) + p(z − z1 ) = 0 .
Теперь мы должны найти точку Q = (x2 , y2 , z2 ) , в которой эта плоскость пересекается с данной прямой. Для этого нужно уравнения данной прямой решить совместно с найденным уравнением плоскости α (см. п. 5.1).
Искомое расстояние d от точки P до прямой l , равное расстоянию между точками P и Q , найдется по формуле
d =  (x1 − x2 )2 +( y1 − y2 )2 +(z1 − z2 )2 .
(x1 − x2 )2 +( y1 − y2 )2 +(z1 − z2 )2 .
Пример 6.
Найти расстояние d от точки P(7,9, 7) до прямой l : x −4 2 = y3−1 = 2z .
Напишем уравнение плоскости, проходящей через точку P и перпендикулярной l. Возьмем в качестве точки M0 (x0 , y0 , z0 ) точку P(7,9, 7) , а в качестве нормального
вектора плоскости |
|
|
|
n = |
|
={4,3, 2}. |
|
l |
|
||
Тогда уравнение плоскости α будет иметь вид: |
|
||
4(x −7) +3( y −9) +2(z −7) = 0, |
|
||
или |
|
|
|
4x +3y +2z −69 = 0. |
(5.5) |
||
Найдем точку пересечения прямой l и плоскости α (см. п. 5.1.). Запишем |
|
||
параметрические уравнения прямой l: |
|
|
|
x = 4t +2, |
|
||
|
|
(5.6) |
|
y =3t +1, |
|||
|
z = 2t. |
|
|
|
|
||
71
и подставим их в уравнение (5.5):
4(4t +2) +3(3t +1) +2 2t −69 = 0,
откуда t = 2.
Подставив t = 2 в (5.6), найдем координаты точки пересечения прямой l и плоскости
α :
x =10, y = 7, z = 4.
Расстояние d от точки P до плоскости α :
d =| M0 P |= (7 −10)2 +(9 −7)2 +(7 −4)2 = 9 +4 +9 = 22.
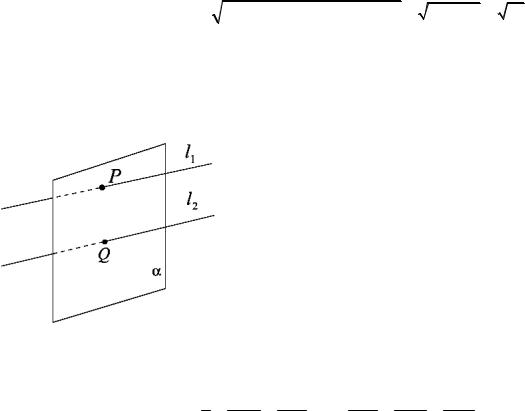
5.7. Расстояние между параллельными прямыми в пространстве
Задачу о нахождении растояния между параллельными прямыми можно свести к задаче, которая рассматривалась в п. 5.6. Точку P выбрать на прямой l1 , затем построить плоскость
α , перепендикулярную прямой l2 и проходящую через точку P , а точка Q будет пересечением прямой l2 и плоскости α . Расстояние между параллельными прямыми будет равным расстоянию между точками P и Q .
Пример 7.
Найти расстояние d между прямыми
l1 : 7x = y +3 2 = z 5−1 и l2 : x7−1 = y 3−3 = z +5 2 .
Заметим, что прямыеl1 и l2 параллельны.
Возьмем в качестве точки P точку, лежащую на прямой l1 : P(0, −2,1) .
Далее, как в примере 6, напишем уравнение плоскости α , проходящей через точку P(0, −2,1) и перпендикулярной прямой l2 :
7(x −0) +3( y +2) +5(z −1) = 0 , или |
|
|
7x +3y +5z +1 = 0 |
(5.7) |
|
Найдем точку пересечения прямой l2 с плоскостьюα . Для этого запишем |
|
|
параметрические уравнения прямой l2 : |
|
|
x = 7t |
+1, |
|
|
+3, |
(5.8) |
y =3t |
||
|
−2, |
|
z =5t |
|
|
подставим в уравнение (5.7): |
|
|
7(7t +1) +3(3t +3) +5(5t −2) +1 = 0,
72

откуда t = 837 .
Подставляя найденное значение t = 837 в уравнения (5.8), получим
x = |
49 |
+1 = |
132 , |
|
|
|
|
|
|
|
|
83 |
|
83 |
|
|
|
|
|
|
|
y = |
21 |
+3 = |
21+3 83 |
, |
|
|
|
|
|
|
|
83 |
|
83 |
|
|
|
|
|
|
|
z = |
35 |
−2 = |
35 −2 83 . |
|
|
|
|
|
|
|
|
83 |
|
83 |
|
|
|
|
|
|
|
Таким образом, координаты точки M0 |
пересечения прямой l и плоскости α : |
|||||||||
|
|
|
|
132 |
, |
270 |
, − |
131 |
|
|
|
|
|
|
M0 |
83 |
83 |
83 |
. |
||
|
|
|
|
|
|
|
|
|||
Искомое расстояние между параллельными прямыми d =| M0 P | .
5.8. Расстояние между скрещивающимися прямыми в пространстве
Скрещивающимися |
прямыми |
называются |
|||||||||||||||||
прямые, которые не пересекаются и не лежат в |
|||||||||||||||||||
одной плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пусть имеются две скрещивающиеся прямые |
|||||||||||||||||||
|
|
|
l : |
x − x1 |
= |
y − y1 |
= |
z − z1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 |
|
|
m1 |
|
|
|
n1 |
p1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
и |
l2 : |
|
x − x2 |
= |
y − y2 |
= |
z − z2 |
|
|||||||||||
|
|
|
|
p2 |
|||||||||||||||
|
|
|
|
|
|
|
|
m2 |
|
|
|
n2 |
|||||||
|
|
|
|
|
|
|
|
|
где M 0 = (x0 , y0 , z0 ) точка |
||||||||||
Строим параллелепипед на векторах l1 , |
l2 и M 0 M1 , |
|
|||||||||||||||||
на прямой l1 , M1 = (x1 , y1 , z1 ) точка на прямой |
|
l2 . |
Тогда расстояние между |
||||||||||||||||
скрещивающимися прямыми l1 и l2 равно высоте параллелепипеда и вычисляется по формуле
|
|
|
|
|
m1 |
|
n1 |
p1 |
|
|
||||
|
|
|
|
|
m2 |
|
n2 |
p2 |
|
|
||||
d = |
Vпар |
= |
|
x2 − x1 |
y2 − y1 |
z2 − z1 |
|
, |
||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
S |
осн |
|
|
|
[ |
l |
, |
l |
] |
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|||||
73

|
|
|
|
|
|
i |
|
|
j |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где [ |
|
, |
|
] = |
m1 |
n1 |
p1 |
, а |
|
[ |
|
, |
|
] |
|
− это длина векторного произведения [ |
|
|
|
] , |
||||||
l1 |
l2 |
|
l1 |
l2 |
|
l1, |
l2 |
|||||||||||||||||||
|
|
|
|
|
m2 |
n2 |
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
численно равная площади параллелограмма, построенного на векторах l1 , l2
Пример 8.
Найти расстояние между скрещивающимися прямыми |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
: |
x −9 |
|
|
= |
y +2 |
= |
|
z |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
−3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
: |
|
|
x |
|
|
|
|
= |
y +7 |
= |
z −2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Направляющий вектор прямой l1 : |
|
|
|
={4, −3,1}, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
l1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
направляющий вектор прямой l2 : |
|
|
|
={−2,9, 2}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Берем точку M0 (9, −2, 0) |
на прямой l1 |
и точку M1 (0, −7, 2) на прямой l2 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тогда |
|
|
|
1 ={−9, −5, 2}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
M0 M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Вычислим объем параллелепипеда, построенного на векторах |
|
, |
|
|
|
|
и |
|
|
|
|
: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
l1 |
l2 |
M0 M1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Vпар = |
|
4 |
|
−3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
9 |
|
|
2 |
= 72 +54 +10 +81+40 −12 = 245. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−9 −5 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Вычислим площадь параллелограмма, построенного на векторах |
|
|
|
и |
|
|
. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
l1 |
l2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Для этого найдем их векторное произведение и вычислим его длину: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
j |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
[ |
|
, |
|
] = |
4 |
|
−3 |
1 |
= |
|
(−6 −9) − |
|
|
(8 +2) − |
|
(36 −6) = −15 |
|
−10 |
|
+30 |
|
. |
||||||||||||||||||||||||||||||||||||||||||||||
|
l1 |
l2 |
k |
k |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
i |
j |
i |
j |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
−2 |
9 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Sосн = |
l1 , l2 |
= |
(−15) |
+ |
(−10) |
+ |
30 |
= |
225 +100 +900 = |
|
|
1225 = 35. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d = |
Vпар |
|
|
= |
245 |
= 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sосн |
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
74
Тема 6. Кривые второго порядка
6.1. Геометрический смысл уравнений |
|
Отметим без доказательства, что уравнение |
|
F(x, y) = 0, |
(6.1) |
связывающее координаты x и y, изображает линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению, и обратно, любая линия на плоскости изображается уравнением
(6.1).
Замечание. В частности, может случиться, что уравнение (6.1) между координатами x и y изображает геометрическое место, состоящее из одной или нескольких отдельных точек. Так, например, уравнение:
x 2 + y 2 = 0
определяет точку O (0, 0); уравнению
(x 2 - 9) 2 + (y 2 - 1) 2 = 0
соответствует геометрическое место, состоящее из четырех точек: (3, 1), (3, -1), (-3, 1), (-3, -1). Кроме того, может случиться, что уравнение (6.1) не определяет никакого геометрического места точек. Так, например, уравнение x 2 + y 2 + 4 = 0
не удовлетворяется ни при каких действительных значениях координат x и y. В этом случае говорят, что уравнению соответствует мнимое место точек.
6.2. Две основные задачи
Из изложенного в 1 и 2 вытекает постановка двух основных задач.
I. Дана линия как геометрическое место точек. Составить уравнение этой линии.
II. Дано уравнение, связывающее координаты x и y. Построить линию, изображаемую этим уравнением.
Мы рассмотрим в дальнейшем соответствующие задачи.
75
6.3. Окружность
Окружность с центром в точке C(a, b) и радиуса R изображается
уравнением: |
|
|
(x - a) 2 + (y - b) 2 |
= R 2 . |
(6.2) |
Раскрывая скобки, придадим уравнению (6.2) вид: |
|
|
x 2 + y 2 – 2ax – 2by + (a 2 |
+ b 2 - R 2 ) = 0, |
(6.2') |
или |
|
|
x 2 + y 2 + Ax + By + C= 0, |
(6.2'') |
|
где |
|
|
A = -2a, B = -2b, C = a 2 + b 2 - R 2 .
Уравнение (6.2'') содержит члены второй и первой степени и свободный член относительно x и y. Такое уравнение называют уравнением второй степени. Итак, окружность изображается уравнением второй степени относительно текущих координат. Но, очевидно, не всякое уравнение второй степени изображает окружность. Действительно, из уравнения (6.2'') видим, что в
уравнении окружности коэффициенты при квадратах координат равны, а член с произведением координат (xy) отсутствует. Обратно, если эти два условия [1) равенство коэффициентов при x 2 и y 2 ; 2) отсутствие члена xy] осуществлены, то уравнение изображает окружность, так как оно приводится к виду (6.2') путем деления на коэффициент при x 2 .
Итак, по виду данного уравнения второй степени мы можем решить, изображает ли оно окружность или нет.
Пример 1.
Уравнение
x2 + y 2 − 4x + 6 y −3 = 0
изображает окружность, так как в нем коэффициенты при квадратах координат равны между собой, а член с произведением координат отсутствует.
Желая построить эту окружность, мы должны предварительно определить координаты ее центра и величину радиуса. С этой целью данное уравнение мы приведем к виду (6.2). Такое преобразование есть ни что иное, как представление (6.2'') в виде (6.2).
Возьмем в данном уравнении члены, содержащие x, т.е. x 2 + 4x, и представим этот двучлен как неполный квадрат разности (x - 2), получим:
x 2 −4 x = (x - 2) 2 – 4.
Далее возьмем члены, содержащие y, т. е. y 2 + 6y, и представим этот двучлен, как неполный квадрат суммы (y + 3), получим:
y 2 + 6y = (y + 3) 2 – 9.
76

После этого данное уравнение запишется так:
(x - 2) 2 – 4 + (y + 3) 2 - 9 – 3 = 0.
Перенося свободные члены вправо, будем иметь:
(x - 2) 2 + (y + 3) 2 = 16.
Сравнивая это уравнение с уравнением окружности
(6.2), видим, что a = 2, b = - 3, R = 4.
Таким образом, центром окружности является точка (2, - 3), и радиус окружности равен 4.
y
-2 |
1 2 |
x
-3 (2,-3)
По этим данным мы можем построить окружность (см. рис. 6.1). |
рис. 6.1 |
6.4. Эллипс
Эллипс есть геометрическое место точек, сумма расстояний которых до двух данных точек есть величина постоянная, равная 2a.
Чтобы составить уравнение эллипса, примем за ось абсцисс прямую, соединяющую две данные точки, а начало координат возьмем в середине между данными точками (рис. 6.2).
Обозначим через 2c расстояние FF' между данными точками. Тогда точки F и F' будут иметь соответственно координаты: (c, 0) и (-c, 0).
Обозначая через x и y координаты произвольной точки M эллипса, выразим по формуле расстояния между двумя точками отрезки FM и F'M:
FM = (x − c)2 + y 2 , F ' M = (x + c)2 + y 2 .
По определению геометрического места точек M имеем:
FM + F' M = 2a
или
(x − c)2 + y 2 + (x + c)2 + y 2 = 2a.
Чтобы искомое уравнение эллипса приняло простейший вид, нужно освободиться от радикалов в этом уравнении.
Перенося один радикал вправо, получим:
(x − c)2 + y 2 = 2a − (x + c)2 + y 2 .
Возводя в квадрат обе части, найдем:
x2 − 2cx + c2 + y 2 = 4a 2 − 4a (x + c)2 + y 2 + x2 + 2cx + c2 + y 2
или
− 4cx = 4a 2 − 4a (x + c)2 + y 2 .
Т. е.
cx + a2 = a (x + c)2 + y 2 .
77

Возводя снова в квадрат, получим:
c2 x2 + 2a2 cx + a4 = a2 (x2 + 2cx + c2 + y 2 )
или
c2 x2 + a4 = a2 x2 + a2 c2 + a2 y 2 ,
т. е.
(a2 −c2 )x2 + a2 y 2 = a2 (a2 −c2 ).
Разделив обе части на a2 (a2 −c2 ) , получим: |
|
|
|||
|
x2 |
+ |
y 2 |
=1. |
(6.3) |
|
a2 |
a2 −c2 |
|||
|
|
|
|
||
Так как c < a, то a2 −c2 - положительная величина (ее принято обозначать через b 2 ), тогда уравнение эллипса будет иметь вид
|
x2 |
+ |
y2 |
=1, |
(6.4) |
|
a2 |
b2 |
|||
|
|
|
|
||
где |
|
|
|
(6.5) |
|
|
b2 |
= a 2 |
− c2 . |
||
Исходя из полученного уравнения (6.4), легко исследовать форму эллипса. Так как уравнение (6.4) содержит только квадраты текущих координат, то оно не изменяется, если изменить знаки одной или обеих координат, следовательно, эллипс симметрично расположен относительно осей OX и OY. Определим сначала точки пересечения эллипса с осями координат. Полагая в уравнении (6.4) y = 0, найдем абсциссы точек пересечения
эллипса с |
осью OX |
: |
|
x2 |
=1 , |
откуда x2 = a 2 |
и x = +a. Эти |
|
две |
точки |
|
|
|
||||||||||
|
|
|
|
a2 |
|
|
|
|
|
|
|
пересечения эллипса с осью симметрии OX |
называются его |
|
вершинами, |
||||||||
расстояние |
между |
|
ними |
равно 2a. Полагая в уравнении (6.4) |
x = 0, |
||||||
найдем ординаты точек пересечения эллипса с осью OY : |
y2 |
|
=1, |
откуда |
|||||||
b2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y2 = b2 , y = +b. Эти две точки пересечения эллипса со второй осью
симметрии OY называют его вершинами, расстояние между ними равно 2b. Если предположить, что a > b, то 2a - длина большой оси симметрии эллипса, 2b – длина малой оси, a и b, следовательно, длины полуосей эллипса. Чтобы исследовать форму эллипса, достаточно считать x и y в уравнении (6.4) положительными, потому что, как было выше замечено, эллипс симметрично расположен относительно осей координат.
Из уравнения (6.4) следует, что
x2 |
≤1, или x ≤ a , |
a2 |
78
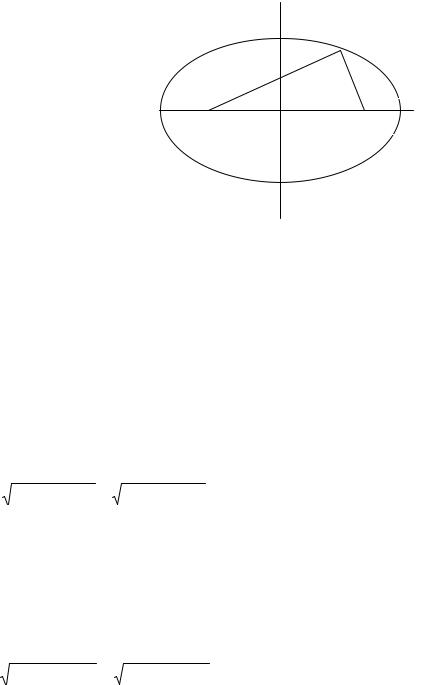
т. е. x может изменяться от 0 до a. С увеличением x от 0 до a, y уменьшается от b до 0. Таким образом, эллипс имеет форму, указанную на рис. 6.2.
Точки F и F' называются фокусами эллипса, расстояние между ними равно 2c. Зная фокусы F и F' и длину 2a большой оси, легко построить эллипс: нужно взять нитку длиной 2a, укрепить два ее конца в точках F и F' и, придав ей форму FMF', описать точкой M эллипс (в точке M поместить карандаш). Если a = b, эллипс обращается в окружность радиуса a.
|
b |
M(x,y) |
|
|
|
||
F′ |
|
|
a |
(-c,0) |
|
(c,0) |
|
|
F |
||
рис. 6.2
6.5. Гипербола
Гипербола есть геометрическое место точек, разность расстояний которых до двух данных точек есть величина постоянная, равная 2a.
Чтобы составить уравнение гиперболы, выберем оси координат так же, как в
6.4. Имеем:
(x + c)2 + y 2 − (x − c)2 + y 2 = 2a,
где 2c есть расстояние FF' между данными точками, называемыми фокусами гиперболы.
Освобождаясь от радикалов, получим, как и в (6.2), уравнение:
x2 |
+ |
y 2 |
=1. |
(6.6) |
|
a2 |
a2 −c2 |
||||
|
|
|
Действительно, перенося первый радикал направо, получим:
(x + c) 2 + y 2 − (x − c) 2 + y 2 = 2a.
Это уравнение отличается от соответствующего уравнения эллипса лишь знаком в левой части. Следовательно, различие совершенно исчезает при возведении обеих частей уравнения в квадрат.
В данном случае c > a, а потому с2 − a2 >0. |
|
Полагая |
(6.6') |
b2 = c2 − a2 , |
запишем уравнение гиперболы:
79
x2 |
− |
y2 |
=1. |
(6.7) |
|
a2 |
b2 |
||||
|
|
|
Оси координат являются двумя осями симметрии, так как x и y входят лишь в квадратах.
Определим точки пересечения гиперболы с осями координат. Полагая в уравнении (6.4') y = 0, найдем абсциссы точек пересечения гиперболы с осью
OX: |
x2 |
=1 , откуда x 2 |
= a 2 , x = +a. Эти две точки пересечения гиперболы с |
|
a2 |
||||
|
|
|
осью симметрии OX называются ее вершинами, расстояние между ними равно 2a. Чтобы найти точки пересечения с осью OY, положим в уравнении (6.7) x = 0. Получим для определения ординат этих точек уравнение:
|
|
|
|
|
|
|
|
− y2 |
=1, |
|
y2 = −b2 , |
|
|
|
|
|
откуда |
|
|
|
|
|
b2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
y = + −b2 = ±b −1 , |
|
|
|
|
|||||
т.е. ординаты точек пересечения |
гиперболы с осью OY |
будут мнимыми |
||||||||||||||
числами: это значит, что ось OY не пересекает гиперболы. Ось OX называется |
||||||||||||||||
действительной осью гиперболы, |
а ось |
OY – ее |
|
|
|
|
||||||||||
мнимой |
осью. |
|
|
b |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
y = ± |
x . |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||
При исследовании |
формы |
гиперболы |
достаточно |
|
|
b |
|
|||||||||
рассматривать положительные x и |
y, |
потому что |
|
|
|
|||||||||||
|
|
|
|
|||||||||||||
кривая |
симметрично |
расположена |
относительно |
|
|
|
|
|||||||||
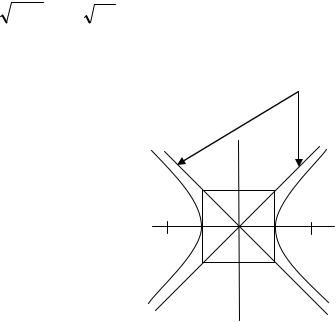
осей координат. Так как из уравнения (6.7) следует, |
-c |
-a |
a |
c |
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что |
x |
≥1, то x может изменяться от a до + ∞. Когда |
|
|
-b |
|
||||||||||
2 |
|
|
|
|||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x увеличивается |
от |
a |
до + |
∞, |
то |
y тоже |
|
|
|
|
||||||
увеличивается от 0 до + ∞.
рис. 6.3
6.6. Парабола
Парабола есть геометрическое место точек, равноотстоящих от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Чтобы составить уравнение параболы, примем за |
ось OX прямую, |
проходящую через данную точку F перпендикулярно |
к данной прямой, за |
80
