
6____2004
.pdfТеорема. При переносе начала координат в точку O′(x0′, y0′) общее уравнение (6.16) преобразуется в уравнение
|
|
|
|
|
|
X |
′T ′ |
′ |
+ |
2b |
′T |
X |
′ |
|
′ |
= 0 , |
(6.24) |
|||
где |
|
|
|
|
|
|
|
A X |
|
|
|
+a33 |
||||||||
′ |
=b + Aa, |
′ |
= a |
T |
Aa +2b |
T |
a +a33 , |
|
|
|
|
′ |
′ |
T |
, при этом инварианты I1 |
, I2 , K3 |
||||
b |
a33 |
|
|
a = (x0 |
, y0 ) |
|
||||||||||||||
не изменяются.
Теорема. Общее уравнение линии второго порядка, заданное в прямоугольной системе координат, переходом к другой прямоугольной декартовой системе координат приводится к одному из следующих типов уравнений:
1. |
λ1 x2 +λ2 y2 +a0 = 0 , где λ1λ2 |
≠ 0 ; |
|
|
2. |
λ2 y2 |
+ 2b0 x0 = 0 , где λ2b0 ≠ 0 ; |
(6.25) |
|
3. |
λ2 y2 |
+c0 = 0 , где λ2 ≠ 0 . |
|
|
|
|
6.9.5.4. Метод вращений |
|
|
Если a12 ≠ 0 , то |
поворотом осей можно |
привести |
квадратичную часть |
|
уравнения (6.16) к сумме квадратов. Действительно, поворот осей на угол ϕ приводит к новому базису e′ = eQ с матрицей перехода
cosϕ |
−sin ϕ |
Q = |
. |
sin ϕ |
cosϕ |
Очевидно, QT Q =QQT = I , т.е. Q − ортогональная матрица. Согласно теореме 2
при переходе к системе координат |
|
′ ′ ′ |
матрица квадратичной части A |
|||||||||
O x y |
||||||||||||
преобразуется в матрицу |
sinϕ a11 |
a12 |
|
|
|
|
||||||
|
cosϕ |
cosϕ |
−sinϕ |
|
|
|||||||
A′ = |
−sinϕ |
cosϕ a |
a |
22 |
sinϕ |
cosϕ , |
|
|
||||
|
|
|
|
|
12 |
|
|
|
|
|
||
при этом |
|
|
|
|
|
|
|
|
|
|
1 |
|
′ |
2 |
|
|
2 |
|
|
|
|
|
|
−a22 )sin 2ϕ . |
|
a12 = −a11 cosϕsinϕ −a12 sin |
|
ϕ +a12 cos |
|
ϕ +a22 cosϕsinϕ = a12 cos 2ϕ − |
2 (a11 |
|||||||
Если cot 2ϕ = (a11 −a22 ) /(2a12 ) , то |
|
′ |
|
. Таким образом при повороте осей на |
||||||||
a12 = 0 |
||||||||||||
такой угол ϕ квадратичная часть уравнения преобразуется в сумму квадратов и уравнение (6.16) в новой системе координат будет иметь вид
′ |
′2 |
′ |
′2 |
′ |
′ |
′ ′ |
+a33 |
= 0. |
(6.26) |
a11 x |
|
+a22 y |
|
+2a13 x |
+2a23 y |
||||
Инварианты I1 , I2 , K3 и полуинвариант K2 |
останутся прежними. |
|
|||||||
91
6.9.5.5. Перенос начала
Далее будем упрощать уравнение (6.26). Если |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
a11 ≠ 0 , то |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
2 |
|
|
′2 |
|
|
|
|
|
|
′ |
|
|
|
|
|
|
′2 |
|
|
||||
′ |
′2 |
|
′ |
′ |
|
|
′ |
|
′2 |
+ |
|
2a13 |
′ |
|
|
|
′ |
|
′ |
+ |
|
a13 |
′ |
− |
a13 |
= x |
′′ |
′ |
+ |
a13 |
|
′ |
|
′′2 |
− |
a13 |
. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
a11 x |
|
+2a13 x |
|
|
= a11 |
x |
|
|
′ |
x |
= a11 |
x |
|
|
|
′ |
|
|
x |
|
′ |
|
= x |
′ |
= a11 x |
|
′ |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
|
|
|
|
|
|
|
|
|
a11 |
|
a11 |
|
|
|
|
|
a11 |
|
|
|
|
|
a11 |
|
|
||||||||||||||
|
|
|
′ |
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если a11 ≠ 0 |
|
и a22 ≠ 0 , то переносом начала |
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′′ = |
x′+ |
|
a13 |
|
|
, y′′ = y′+ |
|
a23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
|
|
|
|
|
|
|
|
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
уравнение (6.26) преобразуется в уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
′′2 |
|
|
′ |
|
|
′′2 |
|
|
|
′ |
= 0, |
|
|
′ |
|
′ |
≠ 0, |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 x |
|
|
+a22 y |
|
|
|
+a33 |
|
a11 a22 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
′ |
|
|
|
|
|
′2 |
|
′ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
a13 |
|
a23 |
, т.е. в уравнение типа 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
a33 |
= a33 |
|
− |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
′ |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a11 |
|
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
равен нулю. |
Если |
|
= 0 , |
|
|
|
, то |
||||||||||||||||||
Пусть один из коэффициентов |
|
′ |
|
|
|
|
|
′ |
|
′ |
|
′ |
≠ 0 |
|||||||||||||||||||||||||||||||||||||||||
a11 |
|
|
|
|
a22 |
|
a11 |
|
a22 |
|||||||||||||||||||||||||||||||||||||||||||||
переносом начала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′′ = x′, |
|
|
y′′ = y′+ |
a23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
уравнение (6.26) преобразуется в уравнение |
|
|
|
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.27) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
′′2 |
|
|
|
′ |
|
|
′′ |
|
|
′ |
|
= 0, |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 y |
|
|
+ 2a13 x |
|
+ a33 |
|
a22 ≠ 0, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
′ |
|
|
|
|
|
′2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
a23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a33 |
= a33 |
|
− |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Когда |
′ |
|
|
≠ 0 , |
|
′ |
= 0 , |
то |
|
|
этот |
|
|
|
случай |
|
|
сводится |
|
к |
предыдущему |
|||||||||||||||||||||||||||||||||
a11 |
|
|
a22 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
переименованием переменных |
|
x |
′′ |
= y |
′ |
|
′′ |
|
|
′ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, y |
|
= x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
что соответствует переходу к новому базису с матрицей перехода |
|
|
|
0 |
1 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Q = |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
Так как Q ортогональная матрица, то числа I1 , I2 , K3 , K2 |
при таком переходе не |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
изменяются.
Дальнейшие преобразования уравнения (6.26) сводятся к преобразованию уравнения (6.27).
Если в этом уравнении a13 = 0 , то уравнение (6.27) относится к уравнению типа 3.
Если же |
a13 ≠ 0 , то |
′ |
′′2 |
|
|
|
|
′ |
|
′ |
′ |
|
′ |
|
′′2 |
|
|
|
′ |
(x |
′′ |
′ |
′ |
и переносом |
||
a11 y |
|
+2a13 x |
+a33 |
= a11 y |
|
|
+2a13 |
|
+a33 |
/ 2a13 ) |
||||||||||||||||
начала |
|
|
|
x |
′′′ |
= x |
′′ |
|
′ |
|
′ |
, y |
′′′ |
= y |
′′ |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
+a33 |
/ 2a13 |
|
|
|
|
|
|
|
|
|
|||||||||
уравнение (6.27) приводится к уравнению |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|||||||||||||
|
|
|
′ |
|
|
′′′2 |
|
|
|
′ |
′′′ |
|
|
′ |
|
|
′ |
≠ 0 |
|
|
|
|
||||
|
|
|
a22 y |
|
|
+2a13 x |
|
= 0, a22a13 |
|
|
|
|
||||||||||||||
которое относится к типу 2.
92
Отметим, что все промежуточные и окончательная системы координат оставались прямоугольными, так как преобразования базиса с помощью ортогональной матрицы перехода сохраняют свойство ортонормированности. Итак, переходом к новой прямоугольной системе координат общее уравнение (6.16) приводится к одному из трех указанных типов уравнений.
Перейдем к вопросу о единственности. Для этого найдем инварианты I2 , K3 для каждого из уравнений (6.25). Имеем для уравнения типа 1
λ |
0 |
λ1 |
0 |
0 |
||||
A = |
1 |
, |
B = |
0 λ2 |
0 |
; |
||
|
0 |
λ2 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
для уравнения типа 2 |
|
|
|
a0 |
||||
|
|
0 |
0 |
b |
|
|||
0 |
0 |
|
||||||
|
0 |
λ2 |
0 |
|
||||
A = |
|
, |
B = |
0 |
; |
|||
0 |
λ2 |
|
|
0 |
0 |
|
||
|
|
|
b0 |
|
||||
для уравнения типа 3 |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
||||
B = 0 λ2 |
0 . |
|||||||
A = |
, |
|||||||
0 |
λ2 |
|
|
|
|
|||
|
|
|
|
|
0 |
|
||
|
|
|
0 |
c0 |
||||
Следовательно,
1.I2 ≠ 0 для уравнения типа 1;
2.I2 = 0, K3 ≠ 0 для уравнения типа 2;
3.I2 = 0, K3 = 0 для уравнения типа 3.
Эти условия взаимно исключают друг друга, и так как общее уравнение (6.16) и уравнения (6.25) имеют одинаковые инварианты I2 , K3 , то общее
уравнение (6.16) приводится только к одному из трех указанных типов уравнений.
Уравнения (6.25) называются приведенными уравнениями линии второго порядка.
Замечание. Особо отметим, что в прямоугольных координатах
коэффициенты |
λ1 , λ2 |
приведенных |
уравнений называются |
|
инвариантами линии, так как |
|
(6.28) |
||
и, следовательно, |
λ1 +λ2 = I1 , λ1λ2 |
= I2 |
||
λ1 , λ2 |
являются |
корнями характеристического |
||
многочлена матрицы A |
λ2 − I1λ + I2 = 0 . |
(6.29) |
||
|
|
|||
93
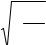
6.9.5.6. Таблица классификации линий второго порядка по инвариантам
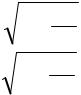
Если общее уравнение (6.16) линии второго порядка задано в прямоугольной декартовой системе координат, то каноническое уравнение линии может быть найдено по инвариантам, так как согласно (6.28) и (6.29) коэффициенты λ1 , λ2 приведенных уравнений являются корнями характеристического многочлена
матрицы A , |
при этом если λ1 ≤ λ2 , |
|
|
то |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a0 = |
K3 |
, b02 = − |
|
K3 |
, c0 |
= |
|
K2 |
. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
|
|
|
|
|
|
|
|
|
|
I1 |
|
|
|
I1 |
|
|
||||||||||
|
Приведем таблицу классификации: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Приведенное |
|
Номер |
|
Каноническое |
|
|
Название линии |
Признак |
||||||||||||||||||||||||||||||||
|
|
уравнение |
|
|
|
|
|
|
уравнение |
|
|
|
|
|
линии |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
линии |
|
|
|
|
|
|
|
||||||||||||||
λ1 x |
2 |
+λ2 y |
2 |
+ |
|
K3 |
= 0, |
1 |
|
|
|
|
|
x2 |
+ |
|
|
|
y2 |
|
|
=1, |
|
|
|
|
Эллипс |
I2 > 0, |
||||||||||||
|
|
|
I2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
a2 |
|
|
b2 |
|
|
|
|
|
|
|
I1K3 < 0 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
λ1λ2 ≠ 0 |
|
|
|
|
|
|
|
a ≥ b > 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
x2 |
|
+ |
|
y2 |
|
= −1 |
|
|
Мнимый эллипс |
I2 > 0, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
b2 |
|
|
|
|
|
I1K3 > 0 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
x2 |
|
+ |
|
|
y2 |
|
|
= 0 |
|
|
|
Пара мнимых |
I2 |
> 0, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пересекающихся |
K3 = 0 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
b2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямых |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
x2 |
|
|
− |
|
|
|
y2 |
|
|
=1 |
|
|
|
|
Гипербола |
I2 |
< 0, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
K3 |
≠ 0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
x2 |
|
|
− |
|
y2 |
|
|
= 0 |
|
|
|
|
Пара |
I2 |
< 0, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пересекающихся |
K3 = 0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
b2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямых |
|
|
I1 y2 ±2 |
− |
K |
3 x |
= |
0, |
6 |
|
|
|
|
|
y2 = 2 px, |
|
|
|
|
Парабола |
I2 |
= 0, |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p > o |
|
|
|
|
|
K3 ≠ 0 |
||||||||||||||||||||
|
|
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
I1K3 ≠ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
I1 y |
2 |
+ |
|
K2 |
|
= 0, |
|
7 |
|
|
|
|
|
|
y2 |
= a2 , |
|
|
|
|
Пара |
I2 = 0, |
|||||||||||||||||
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
a ≠ 0 |
|
|
|
|
|
параллельных |
K3 = 0, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
I1 ≠ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
прямых |
K2 |
< 0 |
||||
94
|
8 |
y2 = −a2 , |
Пара мнимых |
I2 |
= 0, |
|
|
a ≠ 0 |
параллельных |
K3 |
= 0, |
|
|
|
прямых |
K2 |
> 0 |
|
9 |
y2 = 0 |
Пара |
I2 |
= 0, |
|
|
|
совпадающих |
K3 |
= 0, |
|
|
|
прямых |
K2 |
= 0 |
95
Тема 7. Поверхности второго порядка
В данном разделе будут описаны основные поверхности второго порядка, исследование форм поверхностей такого вида будет производиться методом поперечных сечений плоскостями, параллельными координатным плоскостям.
7.1. Эллипсоид и гиперболоид
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
x2 |
|
y 2 |
z 2 |
|
|
||||
|
|
+ |
|
|
+ |
|
|
=1. |
(7.1) |
a |
2 |
b |
2 |
c |
2 |
||||
|
|
|
|
|
|
|
|||
Уравнение (7.1) называется каноническим уравнением эллипсоида.
Рассмотрим сечения данного эллипсоида плоскостями, параллельными координатной плоскости Оху. Каждая из таких плоскостей определяется уравнением вида z = h, а линия, которая получается в сечении, определяется двумя уравнениями:
x |
2 |
+ |
y |
2 |
=1 − |
h |
2 |
|
|
|
|
|
|
, |
|
||||||
a2 |
b2 |
c2 |
(7.2) |
|||||||
|
|
|
||||||||
z = h. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
Отсюда видно, что
1) при условии | h | < c плоскость z = h пересекает эллипсоид по эллипсу с полуосями
a |
* |
= |
a |
1 |
− |
h 2 |
, |
|
c 2 |
||||||
|
|
|
|
|
|
|
|
b |
* |
= |
b |
1 |
− |
h 2 |
, |
|
c 2 |
||||||
|
|
|
|
|
|
|
расположенному симметрично относительно плоскостей Oxz и Oyz;
2)величины а* и b* имеют наибольшие значения при h = 0 (тогда а* = а, b* = b); иначе говоря, самый большой эллипс образуется в сечении координатной плоскостью z = 0;
3)при возрастании | h | величины а* и b* убывают;
96

4) при h = c и h = − c величины а* и b* обращаются в нуль, т. е. эллипс, образуемый сечением эллипсоида (7.1) плоскостью z = c или плоскостью z = − c, вырождается в точку; иначе говоря, плоскости z = c и z = − c касаются эллипсоида;
5) при | h | < c уравнения (7.2) определяют мнимый эллипс; это означает, что плоскость z = h при | h | < c не пересекается с данным эллипсоидом.
Аналогично исследуются сечения эллипсоида плоскостями, параллельными координатным плоскостям Oxz и Oyz (см. рис. 7.1).
рис. 7.1
Величины a, b, c называются полуосями эллипсоида. Если они все различны, эллипсоид называется трехосным. Если эллипсоид образован вращением эллипса вокруг его большей оси, он называется вытянутым эллипсоидом вращения; эллипсоид, образованный вращением эллипса вокруг меньшей оси, называется сжатым эллипсоидом вращения. В случае a = b = c
эллипсоид является сферой. Рассмотрим уравнение
x |
2 |
|
y 2 |
z 2 |
|
|
|||
|
|
+ |
|
|
+ |
|
|
= −1. |
(7.3) |
a |
2 |
b |
2 |
c |
2 |
||||
|
|
|
|
|
|
|
|||
Левая часть его содержит такое же выражение, что стоит слева в каноническом уравнении эллипсоида. Так как это выражение неотрицательно, а справа в уравнение (7.3) стоит –1, то уравнение (7.3) не определяет никакого действительного образа. Уравнение (7.3) ввиду аналогии с уравнением (7.1) называют уравнением мнимого эллипсоида.
Однополостным гиперболоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением
97
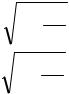
x 2 |
|
y 2 |
z 2 |
|
|
||||
|
|
+ |
|
|
− |
|
|
= 1. |
(7.4) |
a |
2 |
b |
2 |
c |
2 |
||||
|
|
|
|
|
|
|
|||
Двуполостным гиперболоидом называется поверхность, определяемая в некоторой декартовой системе координат уравнением
x |
2 |
|
y 2 |
z 2 |
|
|
|||
|
|
+ |
|
|
− |
|
|
= −1. |
(7.5) |
a |
2 |
b |
2 |
c |
2 |
||||
|
|
|
|
|
|
|
|||
Уравнения (7.4) и (7.5) называются каноническими уравнениями гиперболоидов.
Исследуем однополостный гиперболоид. Рассмотрим сечения его координатными плоскостями Oxz и Oyz. Сечение плоскостью Oxz определяется уравнениями
x2 |
− |
z 2 |
=1, y = 0. |
|
a2 |
c2 |
|||
|
|
Мы видим, что оно представляет собой гиперболу, расположенную симметрично относительно координатных осей Ох, Oz и пересекающую ось
Ох в точках ( a ; 0 ; 0 ) и |
|
( − a ; 0 ; 0 ) . Сечение плоскостью Oyz |
|||
определяется уравнениями |
|
|
|
|
|
|
y 2 |
− |
z 2 |
= −1, x |
= 0. |
|
b 2 |
c 2 |
|||
|
|
|
|
||
Оно представляет собой гиперболу, расположенную симметрично относительно осей Оу, Oz и пересекающую ось Оу в точках (0; b;0 ) и (0;−b;0 ) .
Теперь рассмотрим сечения данного гиперболоида плоскостями z = l, параллельными координатной плоскости Оху. Сечение гиперболоида этой плоскостью определяется уравнениями
|
|
|
x2 |
|
+ |
y 2 |
=1 + |
h2 |
, |
z = |
|
Отсюда видно, что |
|
|
a 2 |
b2 |
c 2 |
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1) любая плоскость z = h |
пересекает |
гиперболоид |
|||||||||
полуосями |
|
|
|
|
h 2 |
|
|
|
|
|
|
a * |
= a |
1 + |
, |
|
|
|
|
||||
|
|
|
|
|
c 2 |
|
|
|
|
|
|
b |
* |
= b |
1 + |
h 2 |
, |
|
|
|
|
||
|
c 2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
h. (7.6)
(7.4) по эллипсу с
98
расположенному симметрично относительно плоскостей Oxz и Oyz;
2) величины а* и b* имеют наименьшие значения при h = 0 (тогда a* = a , b* = b ); иначе говоря, самых малых размеров эллипс образуется в сечении координатной плоскостью z = 0 (он называется горловым эллипсом однополостного гиперболоида);
3) при бесконечном возрастании |h| величины а* и b* бесконечно возрастают
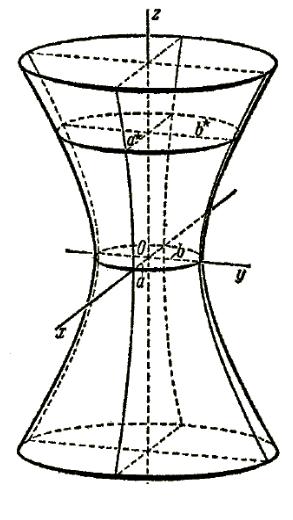
(рис. 7.2).
Сопоставляя изложенное, можем заключить, что однополостный гиперболоид имеет вид бесконечной трубки, бесконечно расширяющейся в обе стороны от горлового эллипса. Однополостный гиперболоид обладает тремя взаимно перпендикулярными плоскостями симметрии; при данном выборе координатной системы эти плоскости совмещены с плоскостями координат.
Величины a, b, c называются полуосями однополостного гиперболоида. Первые две из них (a и b) изображены на рис. 7.2. Чтобы изобразить на чертеже полуось с, нужно было бы построить основной прямоугольник какой-нибудь из гипербол, определяемых сечением однополостного гиперболоида плоскостями Oxz и Oyz.
Заметим, что в случае a = b уравнения (7.6) определяют окружность с центром на оси Oz. Отсюда следует, что при a = b однополостный гиперболоид можно рассматривать как поверхность, образованную вращением гиперболы вокруг одной из осей, а именно той, которая гиперболу не пересекает.
Теперь мы исследуем двуполостный гиперболоид. Рассмотрим сечения его координатными плоскостями Oxz и Oyz. Сечение плоскостью Oxz определяется уравнениями
y 2 |
− |
z 2 |
= −1, |
x = 0 . |
|
b 2 |
c 2 |
||||
|
|
|
Мы видим, что оно представляет собой гиперболу, расположенную симметрично относительно координатных осей Ох, Oz и пересекающую ось Oz в точках (0; 0; с)
рис. 7.2
99
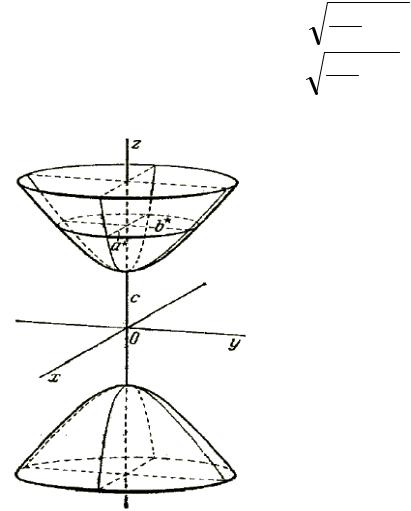
и (0; 0; − с). Сечение плоскостью Oyz определяется уравнениями
x 2 |
− |
z 2 |
= −1, |
y = 0. |
|
a 2 |
c 2 |
||||
|
|
|
Теперь рассмотрим сечения данного гиперболоида плоскостями, параллельными координатной плоскости Оху. Каждая из таких плоскостей определяется уравнением вида z = h, а сечение гиперболоида этой плоскостью определяется уравнениями
x 2 |
+ |
y 2 |
= |
h2 |
−1, |
z = h. |
(7.7) |
|
a 2 |
b2 |
c 2 |
||||||
|
|
|
|
|
Отсюда видно, что
1) при условии | h | > c плоскость z = c пересекает двуполостный гиперболоид по эллипсу с полуосями
a
b
*
*
= |
a |
h 2 |
||
c |
2 |
|||
|
|
|||
= |
b |
h 2 |
||
c |
2 |
|||
|
|
|||
−1 ,
−1 ,
расположенному симметрично относительно плоскостей Oxz и Oyz;
2)при возрастании | h | величины а* и b* возрастают;
3)если | h | возрастает бесконечно, то а* и b* возрастают также бесконечно; 4) если | h |, убывая, приближается к с, то а* и b* также убывают и приближаются к нулю;
при h = c и h = − c имеем: a* = 0, b* = 0;
это означает, что эллипс, образуемый сечением плоскостью z = c или плоскостью z = − c, вырождается в точку, иначе говоря, плоскости z = c и z = − c касаются гиперболоида;
5) при | h | < c уравнения (7.7) определяют мнимый эллипс; это означает, что плоскость z = h при | h | < с с данным гиперболоидом не пересекаются (рис. 7.3).
Сопоставляя изложенное, можем заключить, что двуполостный гиперболоид есть поверхность, состоящая из двух отдельных "полостей" (отсюда его
100
